Description d'un mouvement

ACTIVITES

A1. Nécessité d'un référentiel.

A11. Situation1 :

Prenons l’exemple d'Isaac et Albert, deux voyageurs assis dans un TGV. Isaac voit une vache en train de brouter dans un pré. - Dis donc, Albert : elles courent drôlement vite ici les vaches ! - Mais qu’est-ce que tu dis ? Elle ne bouge pas la vache ! - Mais si, regarde ! Tous les deux, on n’a pas bougé depuis le départ… tu es toujours assis là ! C’est bien la vache qui bouge… - Tu dis n’importe quoi, une vache ne peut pas courir à plus de 200 km/h !!

Alors, que faut-il en conclure : qui a bougé ? Qui n’a pas bougé ?

$\bullet$ La Vache ?

$\bullet$ Isaac ?

$\bullet$ Albert ?

$\bullet$ Le train ?

Conclusion :

A12. Situation2 :

Isaac et Albert décident d’observer les trajectoires décrites par deux points d’une bicyclette :

- Le point B situé sur l’extérieur du pneu avant,

- Le point G, situé sur le guidon.

Chaque point est équipé d’une LED émettant des flashes à intervalle de temps réguliers.

Isaac monte sur le vélo et enregistre les trajectoires à l’aide d’une caméra.

Albert reste sur la piste, et procède de même.

Une fois de retour au laboratoire, ils décident de comparer leurs enregistrements.

A12a. Etude des trajectoires sur l'enregistrement d'Isaac :

- Quelle est la trajectoire décrite par le point G ?

- Quelle est la nature du mouvement du point G ?

- Quelle est la trajectoire décrite par le point B ?

- Quelle est la nature du mouvement du point B ?

A12b. Etude des trajectoires sur l'enregistrement d'Albert :

- Quelle est la trajectoire décrite par le point G ?

- Quelle est la nature du mouvement du point G ?

- Quelle est la trajectoire décrite par le point B ?

- Quelle est la nature du mouvement du point B ?

Conclusion.

Quel est le référentiel dans lequel se situe Isaac ?

Quel est le référentiel dans lequel se situe Albert ?

A2. Différents types de mouvements.

A11. Introduction :

En quelle unité s’exprime une vitesse ?

Quelle est l'unité de mesure d'une distance ?

Quelle est l'unité de mesure du temps ?

En déduire l'unité légale de la vitesse.

En déduire la relation permettant de calculer la vitesse v d’un mobile en fonction de la distance d et du temps t.

A2. Différents types de mouvements.

A21. Introduction :

On a filmé une séquence de la course entre Mario, Luigi et Toad.

Sur chaque véhicule, on a placé une diode émettant un flash à intervalles de temps réguliers : $\Delta t \ = \ 50 \ ms$

L’axe situé en bas de l’enregistrement représente la distance parcourue en mètres par chacun.

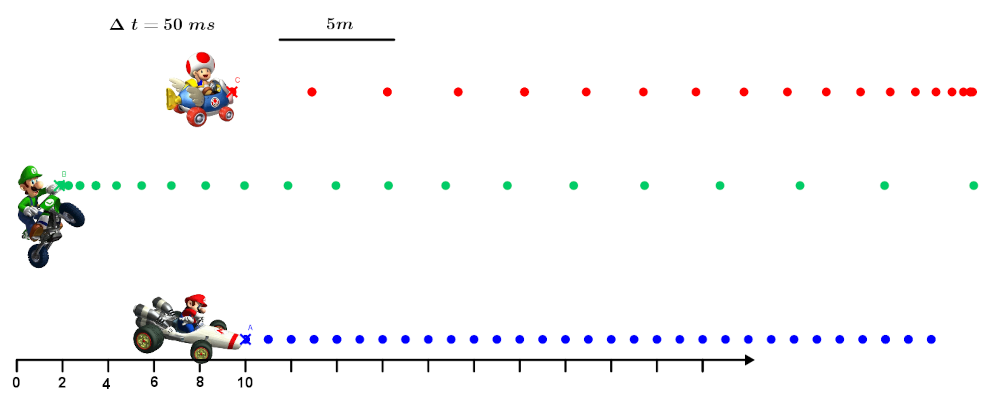
A11a.Etude du mouvement de Mario.

$\bullet$ Mesurer la distance parcourue par Mario entre les points $A_0$ et $A2$.

$\bullet$ Quelle durée correspond à la distance entre ces points ?

$\bullet$ En déduire la vitesse de Mario au point $A_3$

$\bullet$ Reproduire la même démarche entre les points $A_{10} \ et A_{12}$ pour déterminer sa vitesse au point $A_{11}$.

$\bullet$ Reproduire la même démarche entre les points $A_{20} \ et A_{22}$ pour déterminer sa vitesse au point $A_{21}$.

$\bullet$ Comment varie sa vitesse tout au long de l'enregistrement ?

$\bullet$ Quelle est sa trajectoire ?

$\bullet$ Qualifier alors son mouvement pendant la durée de l'enregistrement.

A11b.Etude du mouvement de Luigi.

$\bullet$ Mesurer la distance parcourue par Luigi entre les points $B_7$ et $B9$.

$\bullet$ Quelle durée correspond à la distance entre ces points ?

$\bullet$ En déduire la vitesse de Mario au point $B_3$

$\bullet$ Reproduire la même démarche entre les points $B_{12} \ et B_{14}$ pour déterminer sa vitesse au point $B_{13}$.

$\bullet$ Reproduire la même démarche entre les points $B_{17} \ et B_{19}$ pour déterminer sa vitesse au point $B_{18}$.

$\bullet$ Comment varie sa vitesse tout au long de l'enregistrement ?

$\bullet$ Quelle est sa trajectoire ?

$\bullet$ Qualifier alors son mouvement pendant la durée de l'enregistrement.

A11c.Etude du mouvement de Toad.

$\bullet$ Mesurer la distance parcourue par Luigi entre les points $C_0$ et $C_2$.

$\bullet$ Quelle durée correspond à la distance entre ces points ?

$\bullet$ En déduire la vitesse de Mario au point $C_1$

$\bullet$ Reproduire la même démarche entre les points $C_{5} \ et C_7$ pour déterminer sa vitesse au point $C_{6}$.

$\bullet$ Reproduire la même démarche entre les points $C_{11} \ et C_{13}$ pour déterminer sa vitesse au point $C_{12}$.

$\bullet$ Comment varie sa vitesse tout au long de l'enregistrement ?

$\bullet$ Quelle est sa trajectoire ?

$\bullet$ Qualifier alors son mouvement pendant la durée de l'enregistrement.

A22. Plus précisément, à l'aide du logiciel "Tracker" .

A22a. La course.

$\bullet$ Pour chaque participant, pointer le déplacement correspondant.

$\bullet$ Représenter graphiquement les variations de leur déplacement en fonction du temps.

$\bullet$ Représenter graphiquement les variations de leur vitesse en fonction du temps.

$\bullet$ Pour chacun, déterminer l'expression temporelle de leur vitesse.

A22b. Retour chez Isaac et Albert.

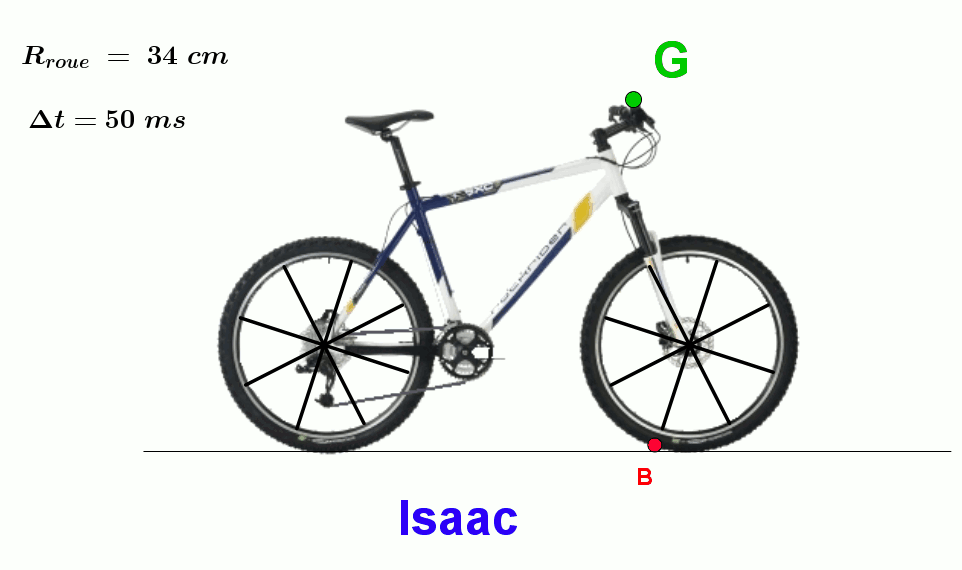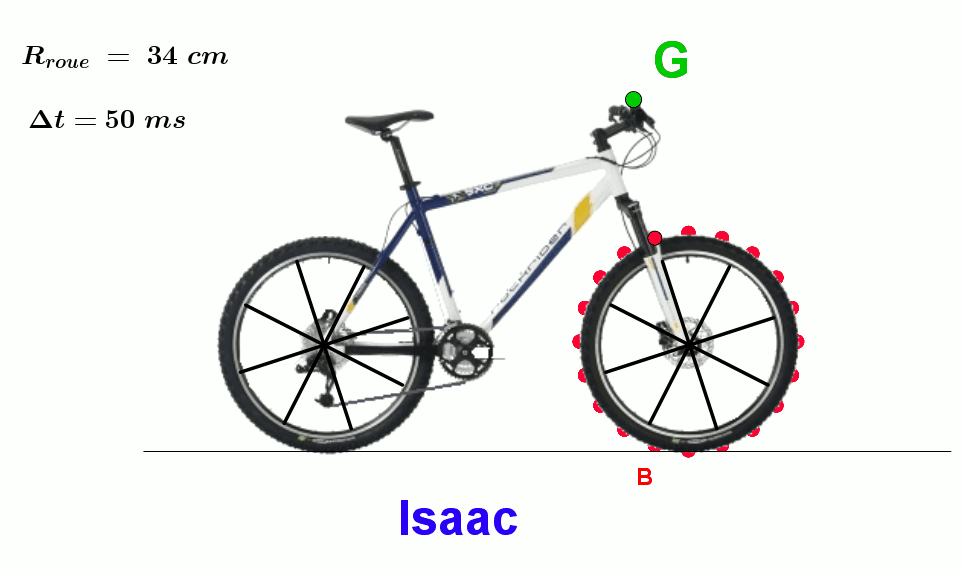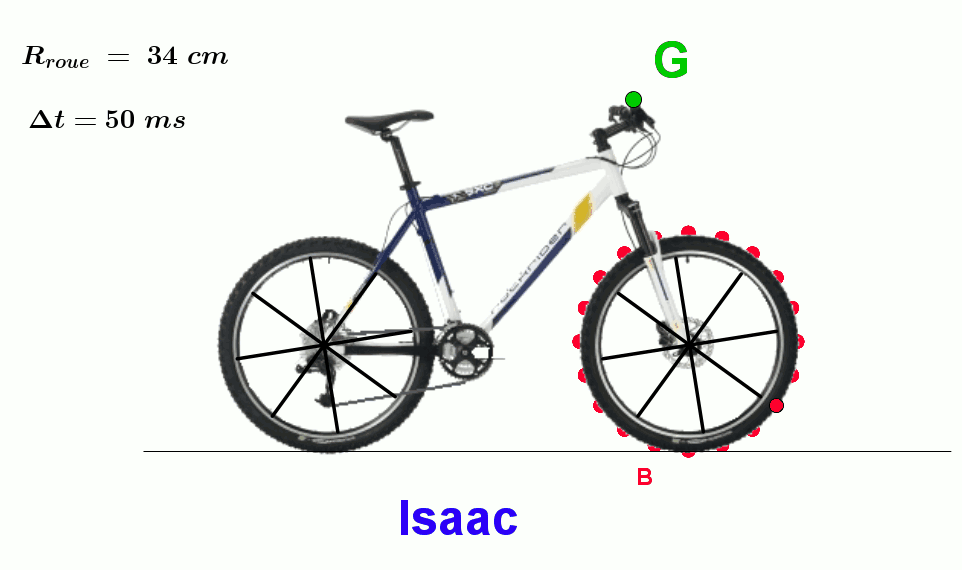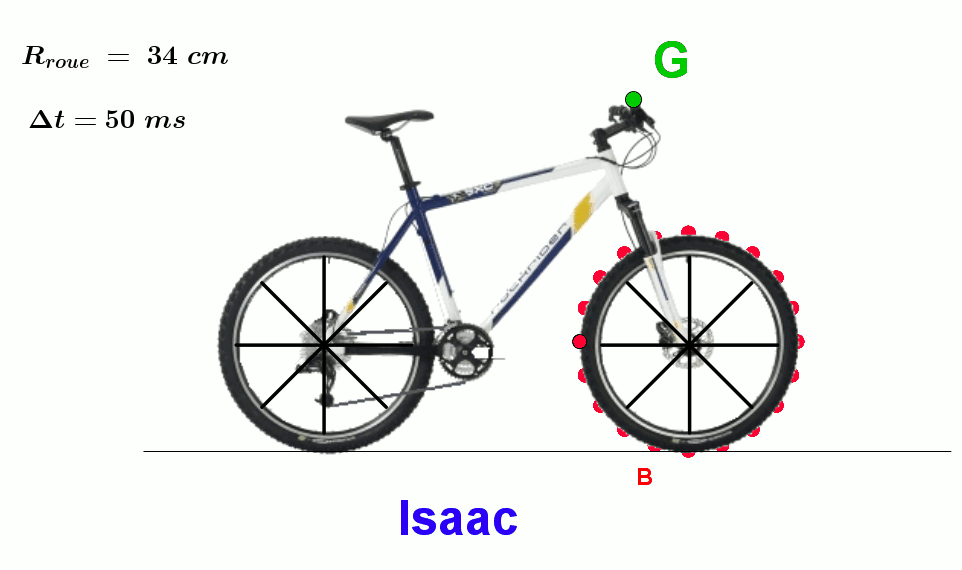
$\bullet$ Effectuer le pointage du point B.

$\bullet$ Combien de tours effectue le point B par seconde.

$\bullet$ Déterminer la valeur de l'angle parcouru par le bon B par seconde.

$\bullet$ Comment qualifier cette grandeur ?

$\bullet$ En utilisant la valeur du rayon de la roue, déterminer la relation reliant la vitesse et la valeur déterminée précédemment.

COURS

C1. Référentiel et repère.

	Dans un référentiel terrestre, les avions et les pilotes sont en mouvement. Dans le référentiel des avions, les pilotes sont immobiles.
Le repère d'espace est constitué de deux axes, et d'une base de temps permettant de connaître la position du mobile à un instant donné.

C2 Nature de la trajectoire.

	Le ballon a une trajectoire parabolique dans le référentiel terrestre
	Le point extérieur de la roue a une trajectoire circulaire dans le référentiel lié au vélo.
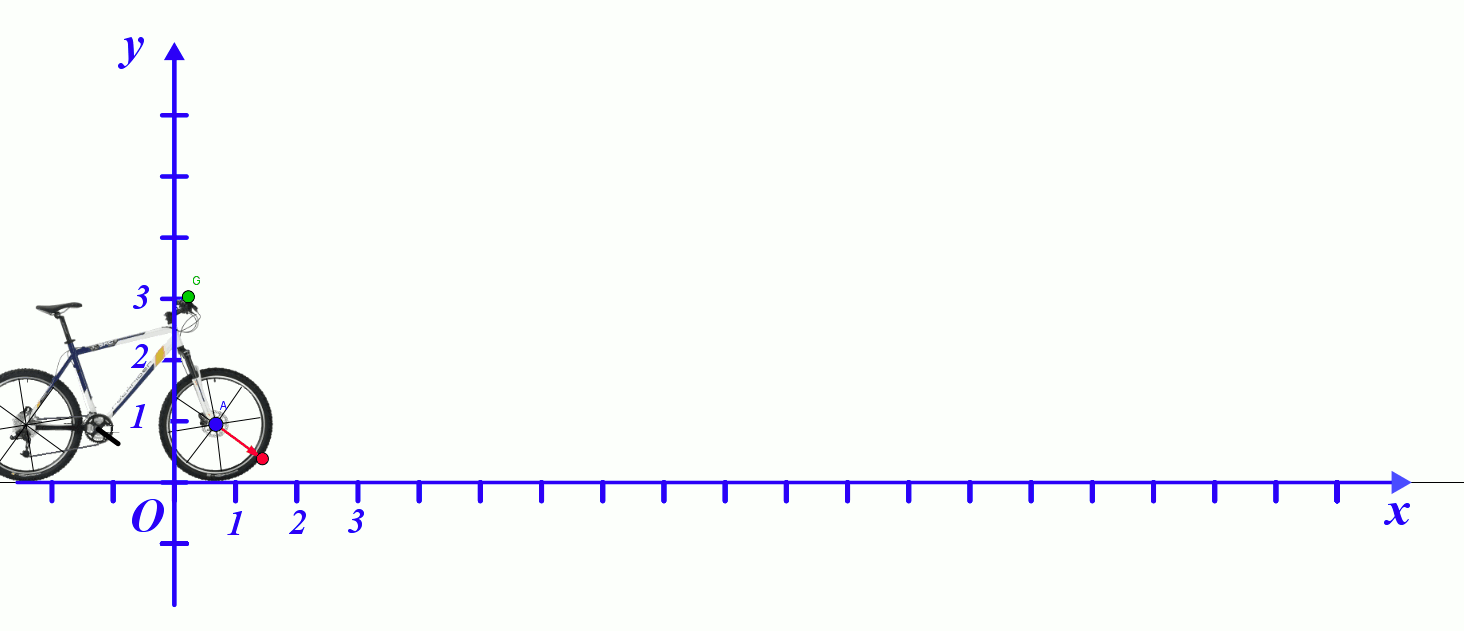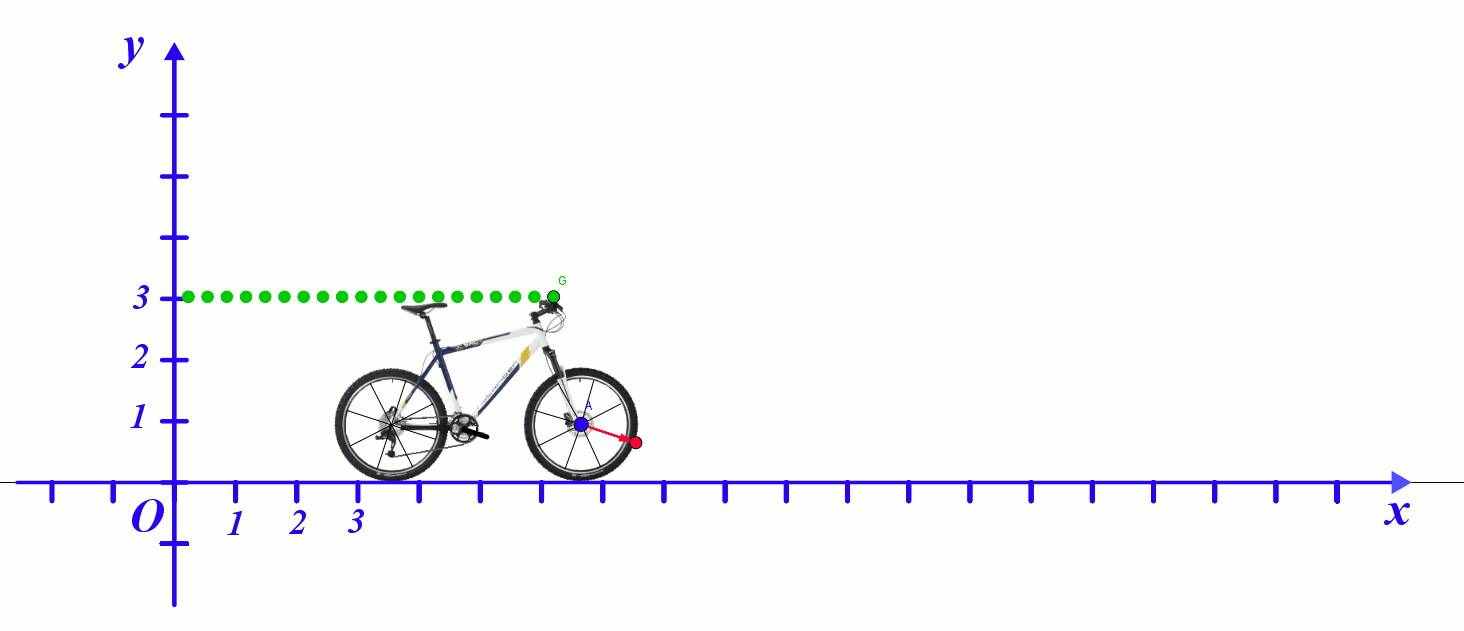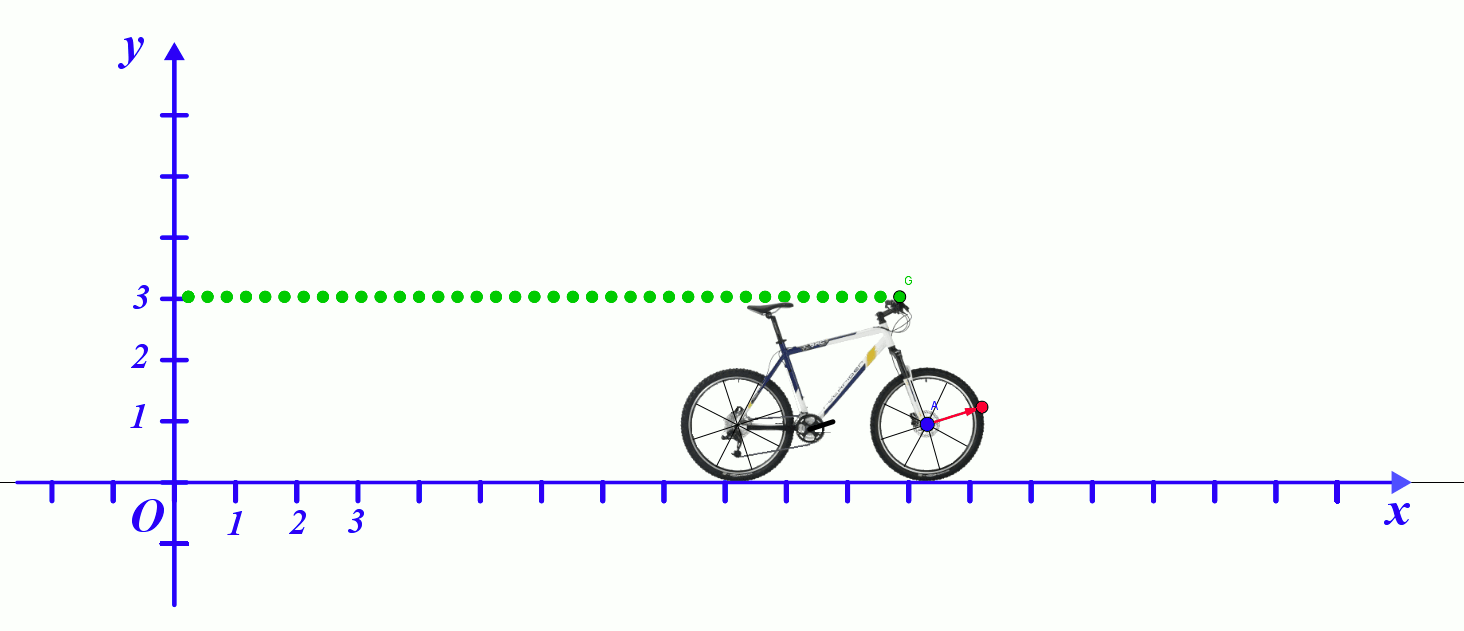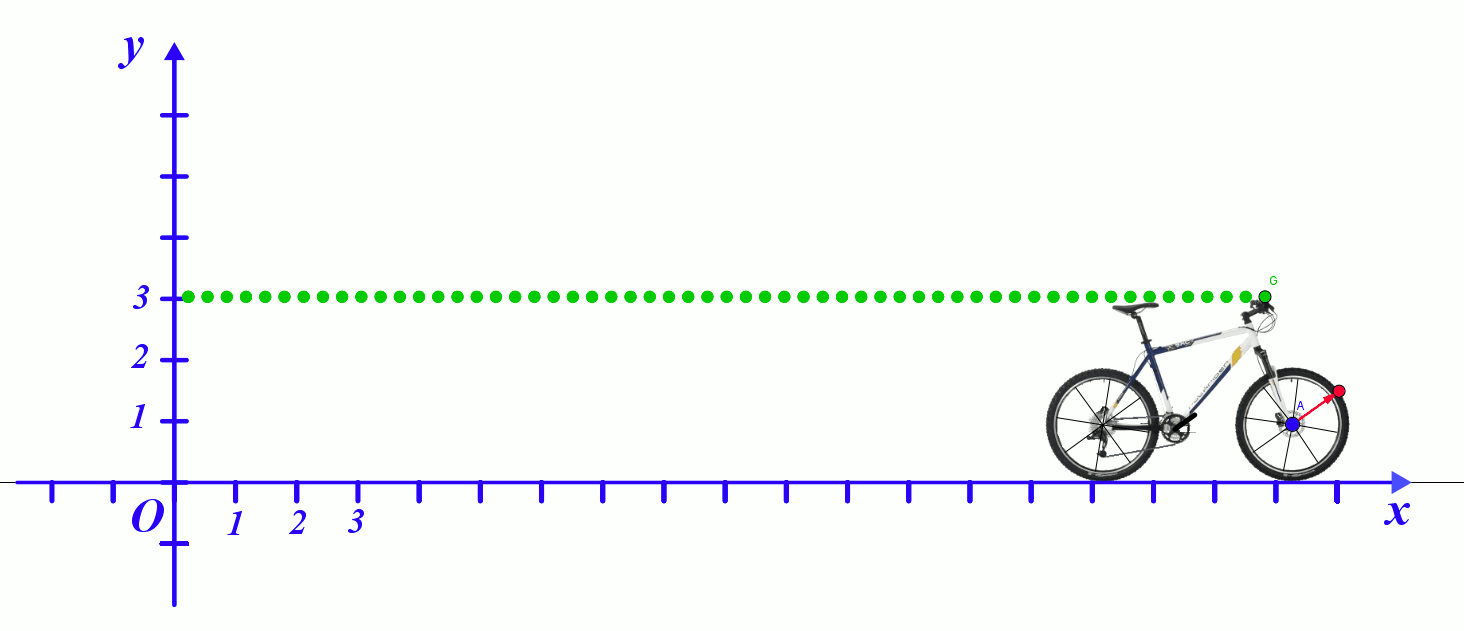	Le point du guidon a une trajectoire rectiligne dans le référentiel terrestre.

C3. Vitesse moyenne.

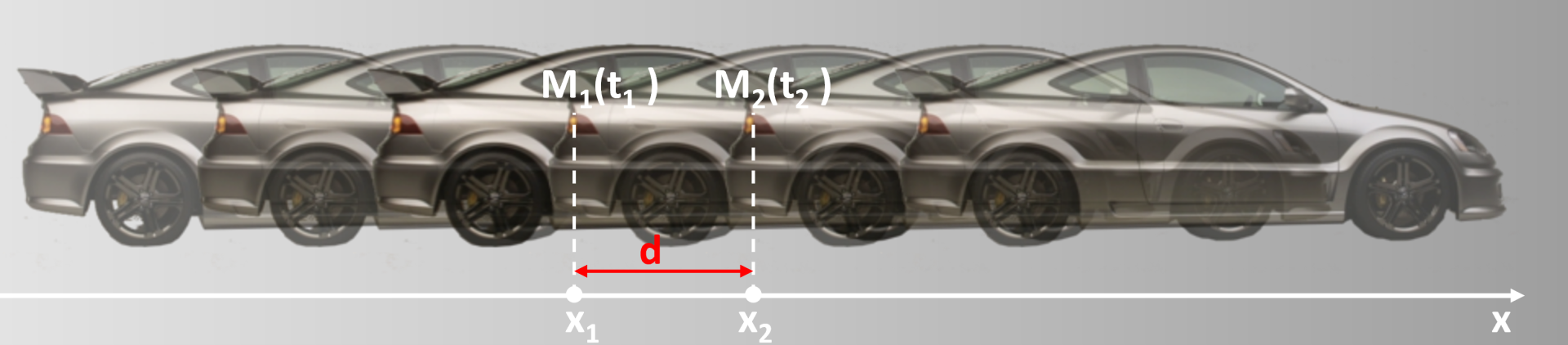
La distance $\Delta \ d$ parcourure entre les points $M_1$ et $M_2$ est : $\Delta \ d = M_2-M_1$

La durée $\Delta \ t$ parcourure entre les instants $t_1$ et $t_2$ est : $\Delta \ t = t_2-t_1$

La vitesse instantanée entre les points $M_1$ et $M_2$ est : $v \ = \ \dfrac{\Delta \ d}{\Delta \ t} \ = \ \dfrac{M_2-M_1}{ t_2-t_1}$.

C4. Nature du mouvement.

C41. Mouvements rectilignes.

C41a. Mouvement rectiligne uniforme.

Au cours d'une même durée, la distance parcourue est la même. La vitesse est constante.

C41b. Mouvement rectiligne accéléré.

Au cours d'une même durée, la distance augmente. La vitesse augmente

C41c. Mouvement rectiligne ralenti.

Au cours d'une même durée, la distance diminue. La vitesse diminue.

C41d. Conclusion.

C42. Mouvements circulaires uniformes.

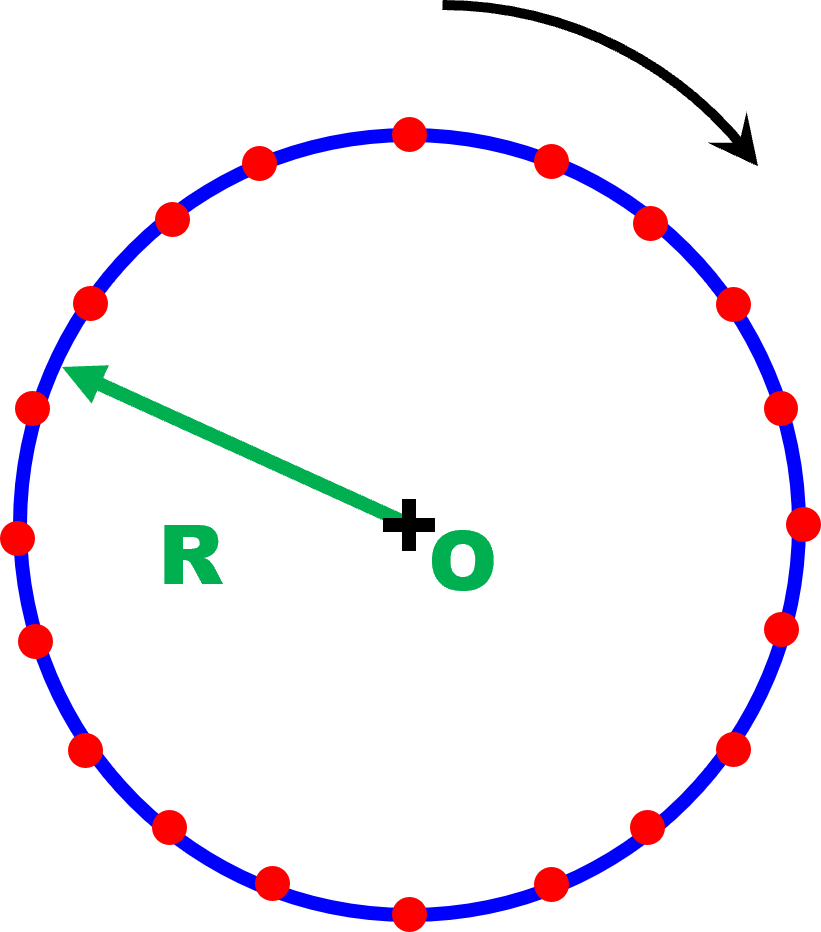Dans le cas d'un mouvement circulaire uniforme autour d'un point $O$, la vitesse $v$ d'un point $M$ est constante.   La fréquence de rotation $\omega$ correspond à l'angle balayé par le rayon en fonction du temps.   Elle s'exprime en RADIANS PAR SECONDE (rad/s).   La relation liant ces deux grandeurs est : $v \ = \ R \times \ \omega$