Vision et Images
ACTIVITES
A1. Les lois de Snell-Descartes.
|
Ci-contre, la photographie d'un verre posé sur un miroir, rempli d'eau et dans lequel est placée une paille. Comment expliquer les observations ? |
 |
|
|
|
Doc 3 :Matériel à disposition.
|
|
Doc 3 : Incertitude-type par méthode statistique. On mesure $n$ mesures d'une grandeur $X$ avec différentes valeurs $\left \{ X_1 \ ; \ X_2 …… X_n \right \}$. L'estimation de l'incertitude-type est : $U \left ( X \right ) \ = \ \dfrac{\sigma}{n}$ où $\sigma$ représente l'écart-type. |
$\bullet$ A l'aide du matériel à disposition, réaliser le protocole suivant :
|
$\bullet$ A l'aide du matériel à disposition, réaliser le protocole suivant : $\surd$ Placer la source lumineuse, de sorte que le rayon lumineux suive la ligne 0°/0°. $\surd$ Placer le miroir le long de la ligne 90°/90°. $\surd$ Le rayon réfléchi doit suivre cette même ligne. $\surd$ Effectuer les mesures nécessaires. |
|
$\bullet$ Conclusion.
$\bullet$ A l'aide du matériel à disposition, réaliser le protocole suivant pour deux prismes différents (plexiglas et différents liquides).
$\surd$ Placer la source lumineuse, de sorte que le rayon lumineux suive la ligne 0°/0°.
$\surd$ Placer le prisme le long de la ligne 90°/90°.
$\surd$ Le rayon réfléchi doit suivre cette même ligne (il doit "revenir" à son point de départ)
$\surd$ Le rayon réfracté doit suivre cette même ligne.
$\surd$ Effectuer les mesures de l'angle du rayon incident i1 et de l'angle du rayon incident i2. Effectuer une analyse des mesures à l'aide d'un logiciel de saisie.
A2. La lentille mince convergente.
L'appareil photo permet de reproduire l'image d'un objet et de l'enregistrer. De même, le vidéoprojecteur renvoie à distance une image enregistrée..
Comment fonctionnent ces appareils ?
|
|
|
Doc 3 :Construction de l'image réelle d'un objet formée par une lentille mince.
|
|
|
A21. Observations.
$\bullet$ Manipuler les différentes lentilles à votre disposition et noter la différence notable entre chacune.
$\bullet$ Pour chaque type, tenter d'obtenir une image des lampes du plafond sur le sol. Observation.
$\bullet$ En utilisant celles permettant de projeter les lampes, en choisir deux différentes. Observation.
$\bullet$ Qu'appelle-t-on le "foyer" d'une lentille ?
$\bullet$ Qu'appelle-t-on la distance focale d'une lentille ?
A22. Manipulation.
$\bullet$ Positionner le matériel sur le banc (source, objet, lentille, écran) de sorte à obtenir une image nette de l'objet.
$\bullet$ Mesurer :
$\surd$ Les positions de l'objet et de l'image obtenue par rapport à la lentille.
$\surd$ Les tailles de l'objet et de l'image.
NB : on fera attention à respecter l'orientation du plan (abscisse, ordonnée)
$\surd$ ompléter le schéma ci-dessous :

$\bullet$ Pour différentes positions de l'objet, effectuer le rapport de la taille de l'image à celle de l'objet, puis le rapport de leurs positions à la lentille.
$\bullet$ Ainsi, pour différentes positions de l'objet, tenter de déterminer la position de l'image. Vérifier.
$\bullet$ De même, pour différentes positions de l'image, tenter de déterminer la position de l'objet. Vérifier.
A22. L'œil.
$\bullet$ Identifier chaque partie de l'œil :
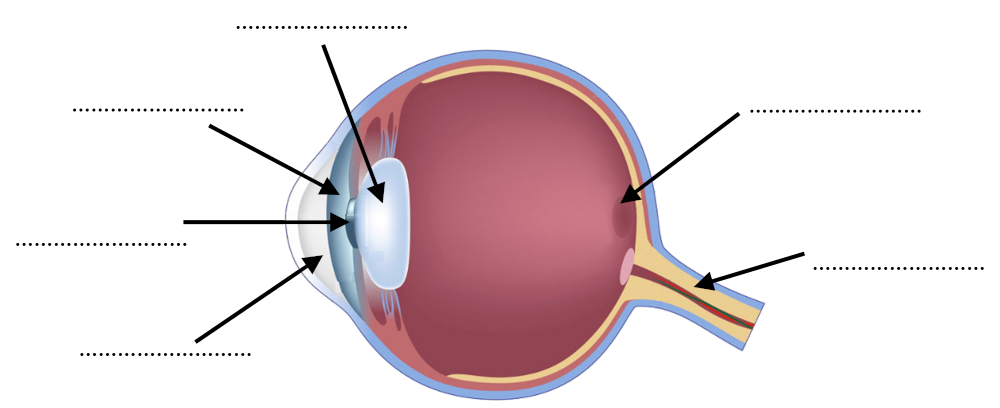 |
$\bullet$ Rétine $\bullet$ Cristallin $\bullet$ Nerf optique $\bullet$ Iris $\bullet$ Cornée $\bullet$ Pupille |
$\bullet$ Associer à chaque partie de l'œil à celle du montage ci-dessous en plaçant une lentille, un diaphragme et un écran. Proposer une association du matériel aux constituants de l'œil.

$\bullet$ Noter l'orientation de l'image. Conclure.
$\bullet$ En supposant ce montage comme la représentation d'un œil, former une image nette sur l'écran, puis décaler l'objet légèrement. Quel est alors le paramètre non modifiable pour que l'image redevienne nette ? Proposer comment résoudre le problème.
Exercices P233 à 243 :
13 ; 15 ; 17 ; 19 ; 22 ; 24 ; 31 ; 33 ; 36 ; 40 ; 41 ; 44
COURS
C1. Emission et propagation de la lumière.
C11. Propagation rectiligne.
|
La lumière se propage en ligne droite dans le vide et dans les milieux matériels transparents. C'est le phénomène de propagation de la lumière.
Son trajet est modélisé par un rayon de lumière, représenté par une droite fléchée.
Lorsque la lumière change de milieu, à la séparation des milieux, sa direction change : c'est la réfraction Une partie de la lumière n'est pas réfractée et reste dans le même milieu : c'est la réflexion. |
 |
C12. Vitesse de la lumière.
C12a. Valeur.
La lumière se propage dans le vide et dans l'air à la vitesse $c \ = \ 299.792.458 \ = \ 3,0.10^{ \ 8} \ m.s^{ \ -1}$.
C'est sa valeur de propagation la plus grande.
C12b. Indice de réfraction.
Lorsque la lumière subit la réfraction, la vitesse de propagation est modifiée.
L'indice de réfraction, ou indice optique est le rapport de sa vitesse dans le vide c et v sa vitesse de propagation dans le milieu considéré.
|
$c$ et $v$ en $m.s^{ \ -1}$ $n$ sans unité. |
C2. Réflexion et réfraction.
C21. Lois de Snell-Descartes pour la réflexion.
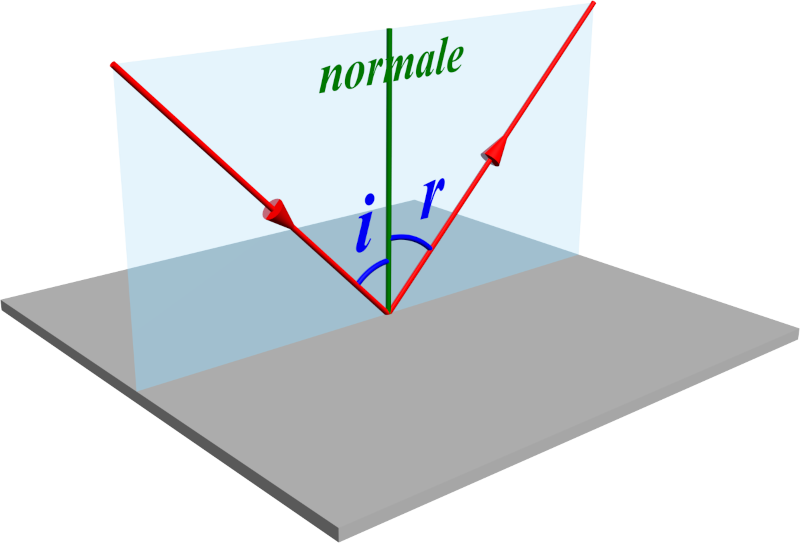 |
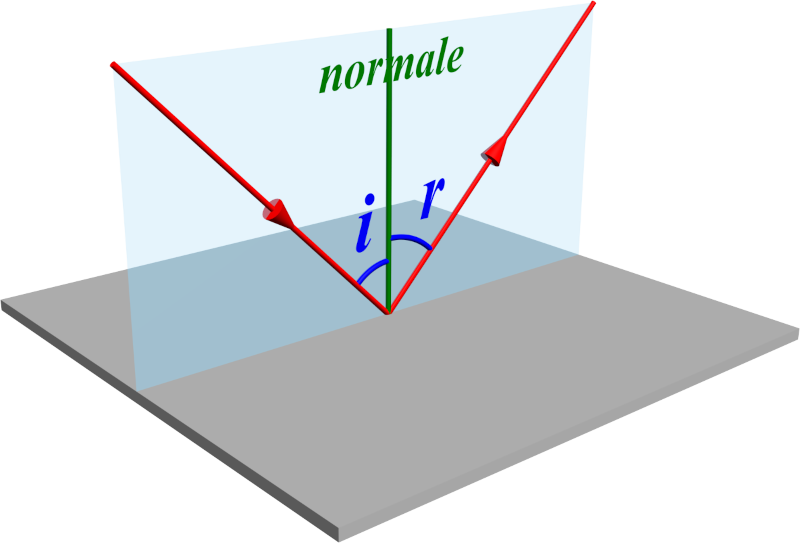
La lumière qui parvient à la surface de séparation entre deux milieux, elle est réfléchie par cette surface.
Le rayon incident formant un angle $\color{blue}{i}$ avec la normale à la surface est réfléchi en un rayon réfracté formant un angle $\color{blue}{r}$ avec cette même normale : $\color{blue}{i \ = \ r}$ |
C22. Lois de Snell-Descartes pour la réfraction.
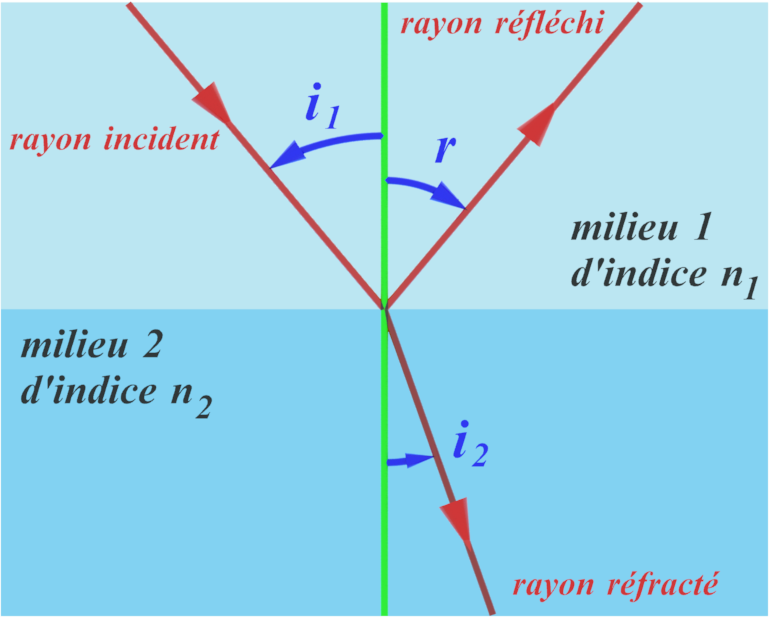 |
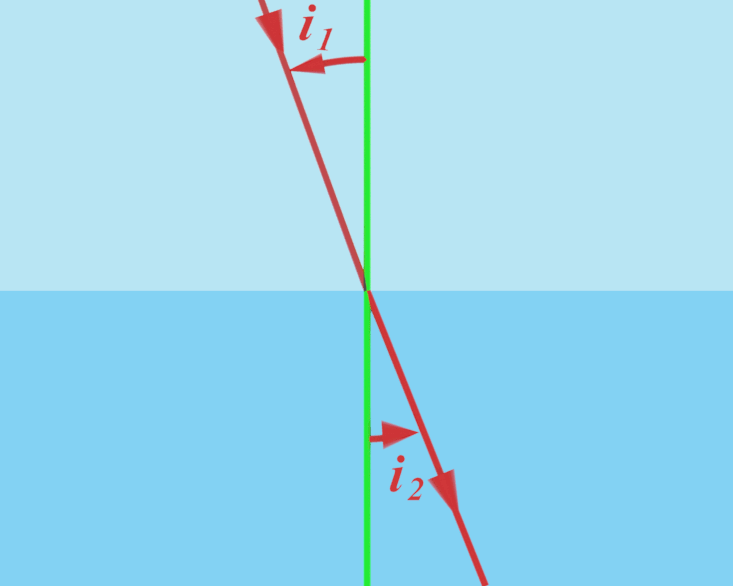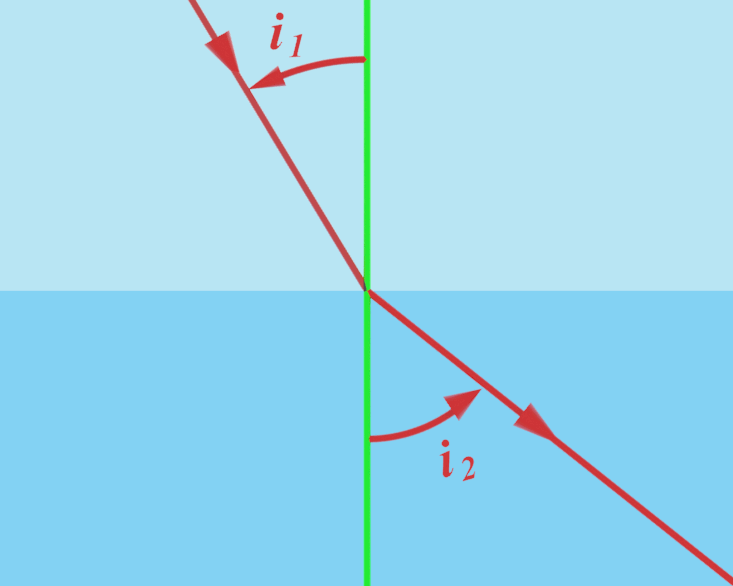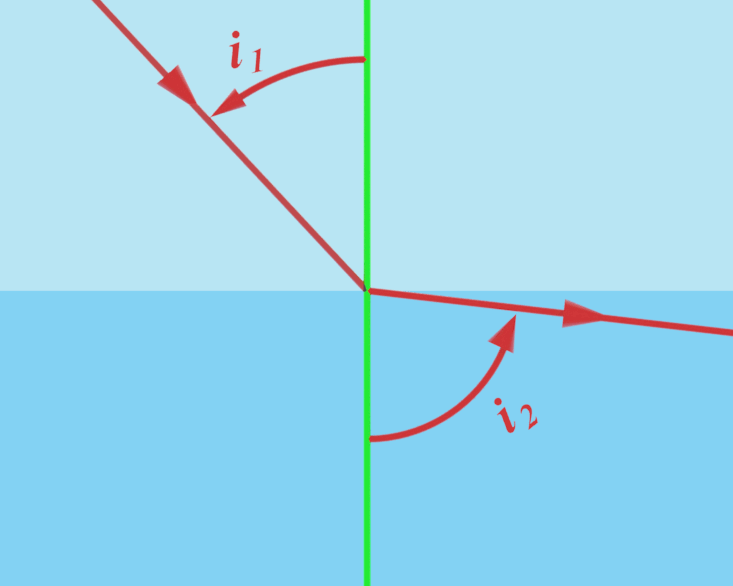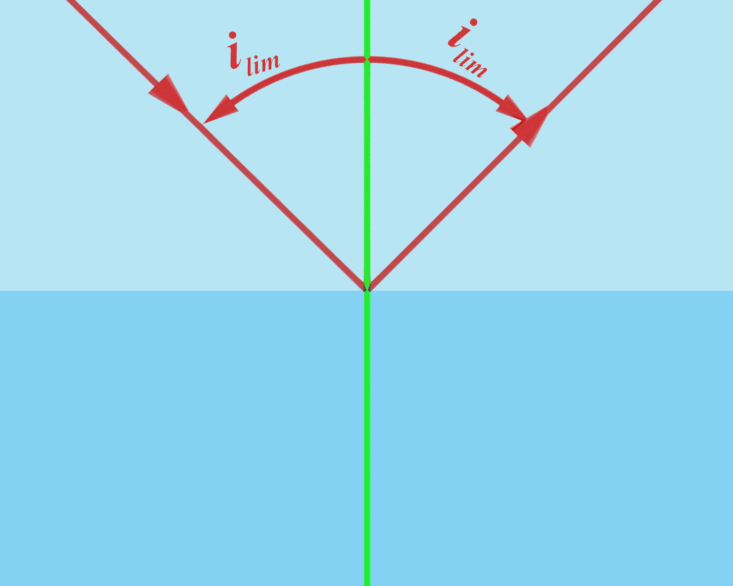
Lors du changement de milieu, la direction de propagation est modifiée. Le rayon incident est dévié en un rayon réfracté.
$\color{blue}{i_1}$ étant l'angle entre le rayon incident et la normale à la surface de séparation, le rayon réfracté forme alors un angle $\color{blue}{i_2}$ avec la normale. $\color{red}{n_1 \ \times \ sin \left ( i_1 \right ) \ = \ \ n_2 \ \times \ sin \left ( i_2 \right )}$
Où $n_1$ et $n_2$ sont les indices de réfraction de chaque milieu. |
C23. Réflexion totale.
|
Lors du passage d'un milieu d'indice $n_1$ à un milieu d'indice $n_2$ inférieur à $n_1$, la réfraction n'est observée que pour une valeur limite de l'angle d'incidence. C'est le phénomène de réflexion totale. Il a lieu pour une valeur de l'angle d'incidence $\color{red}{i_{ \ 1} \ = \ Arcsin \left ( \dfrac{n_2}{n_1} \right )}$ |
 |
C3. Lentilles convergentes.
C31. Caractéristiques.
C31a. Description.
|
Une lentille est un objet transparent capable de réfracter la lumière sur deux surfaces.
Une lentille convergente est plus fine en ses bords qu'en son centre. Une lentille divergente est plus fine en son centre qu'en ses bords. |
 |
|
On modélise une lentille par une double flèche : |
 |
C31a. Description.
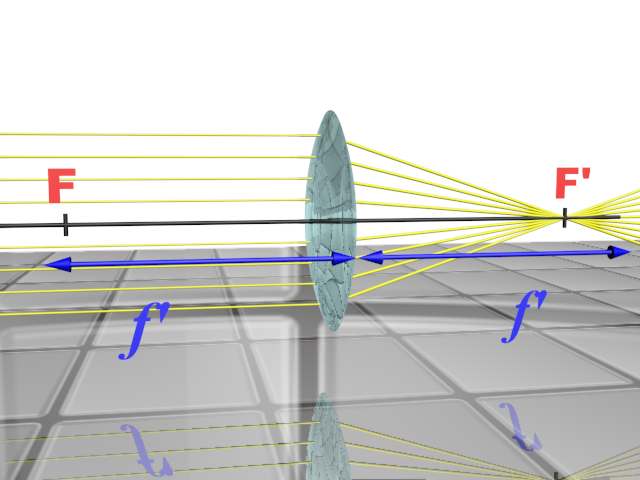
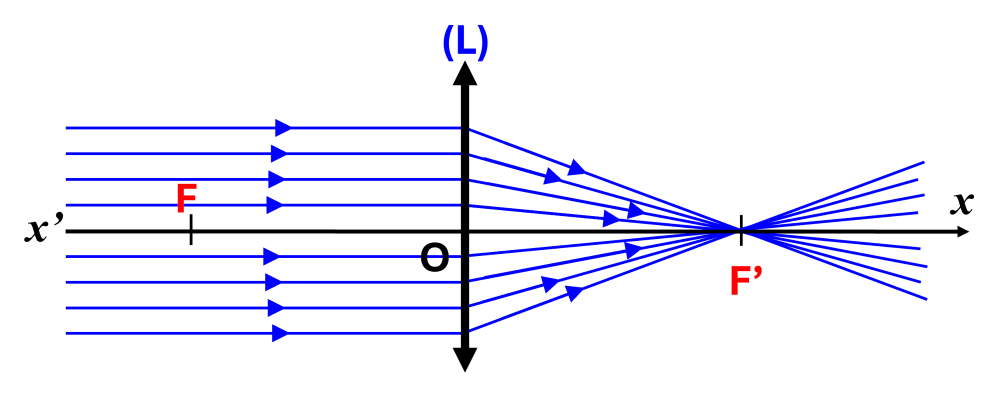
$\bullet$ Une lentille convergente présente un axe de symétrie passant par son centre $O$ : l'axe optique $\left (xx'\right )$.
$\bullet$ Elle focalise tous les rayons parallèles à l'axe en un point appelé foyer image F'.
$\bullet$ La distance entre son centre et son foyer image $OF$ est appelée distance focale image.
$\bullet$ Elle possède un foyer objet $F$ situé à la même distance $OF \ = \ OF'$ de son centre.
C32. Construction de l'image.
On construit l'image d'un objet AB en traçant trois rayons particuliers :
$\bullet$ Le rayon issu du point $B$ passant par le centre optique $O$ n'est pas dévié.
$\bullet$ Le rayon issu du point $B$ et parallèle à l'axe optique émerge de la lentille en passant par son foyer image $F'$.
$\bullet$ Le rayon issu du point $B$ passant par le foyer $F$ émerge parallèlement à l'axe optique.
$\bullet$ Les trois rayons se croisent en un même point $B'$, image de $B$.
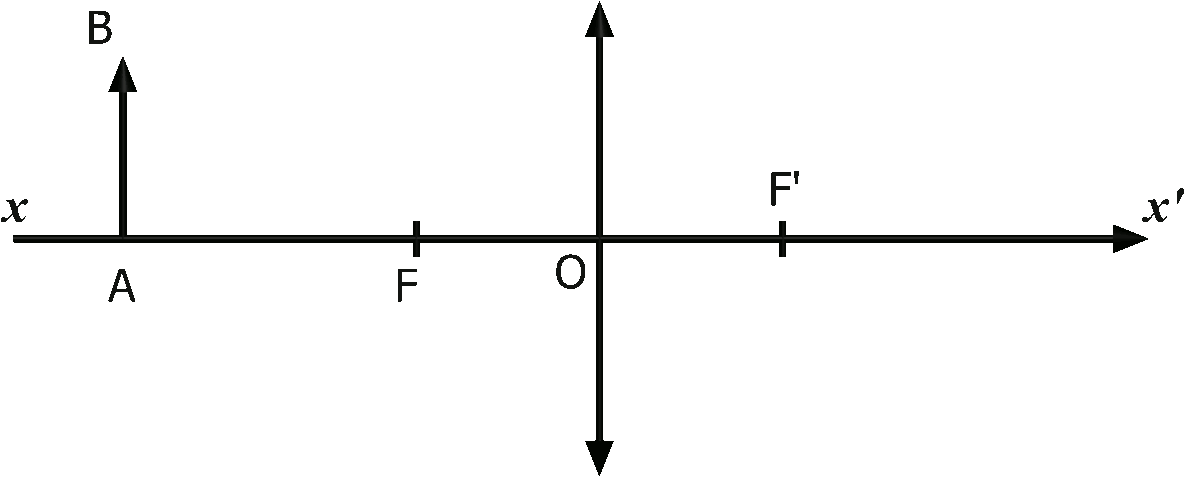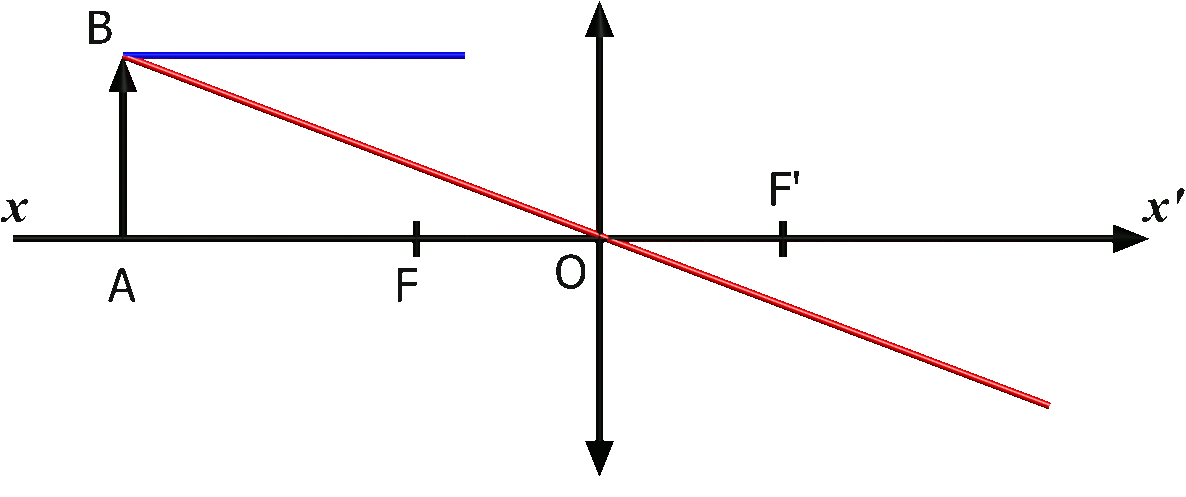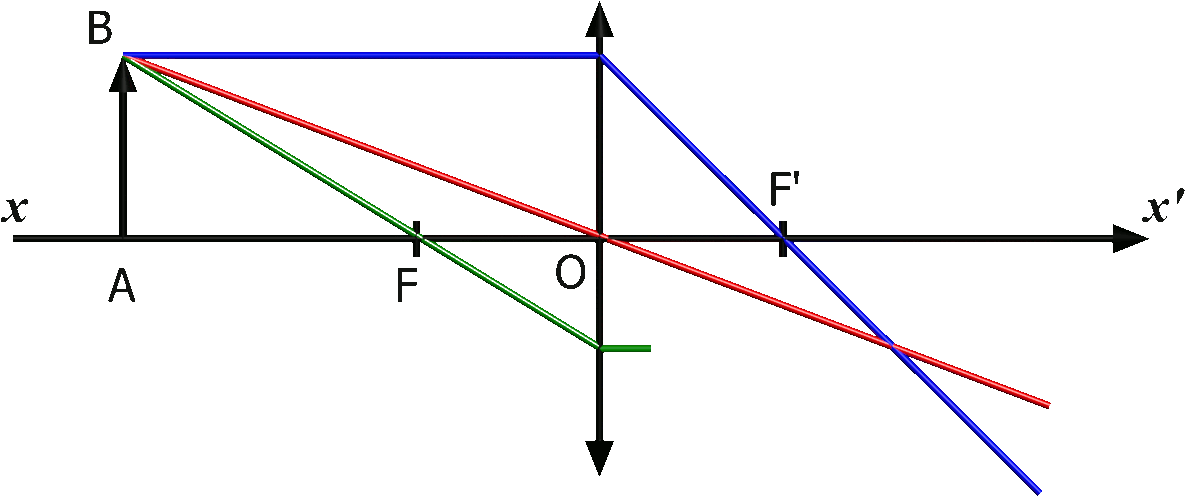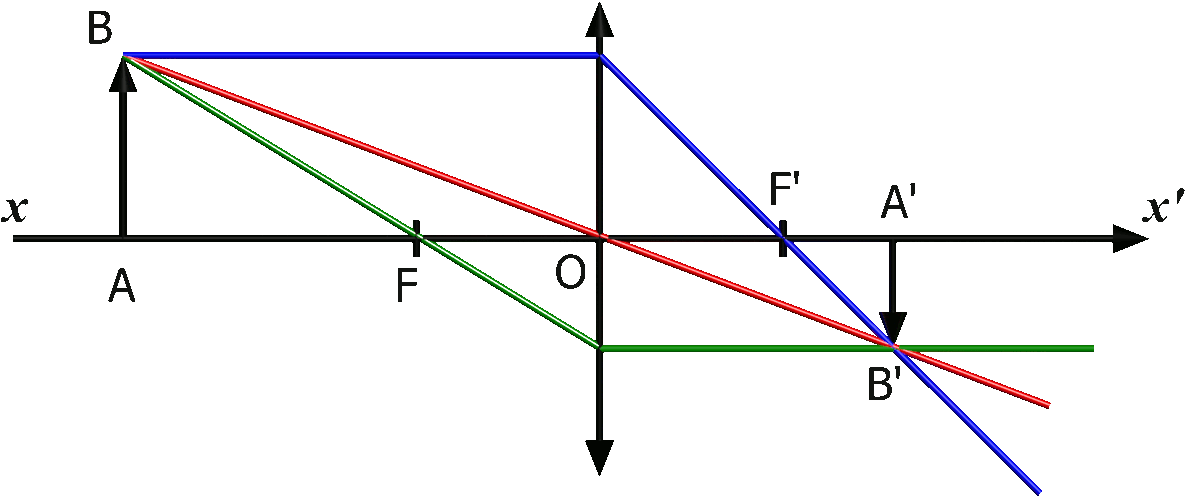
NB :l'image est dans l'autre sens que celui de l'objet, on parle d'image renversée.
C33. Grandissement.
On définit le grandissement $\gamma$, la grandeur sans unité par la relation : $\color{red}{\gamma \ = \ \dfrac{A'B'}{AB}}$
$\bullet \ si \ \gamma \ > \ 1$, l'image est plus grande que l'objet.
$\bullet \ si \ \gamma \ < \ 1$, l'image est plus petite que l'objet.
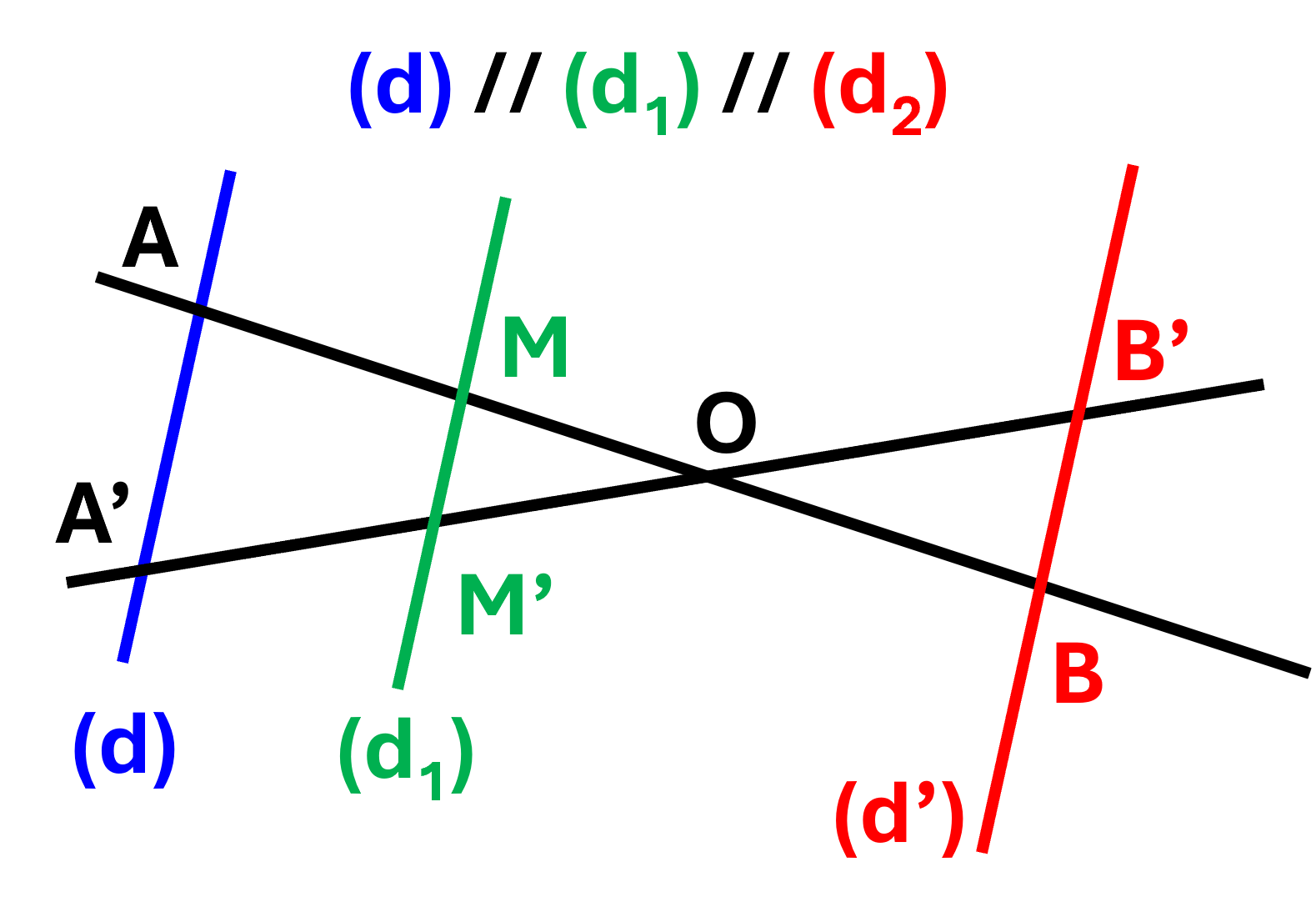
NB : L’objet et l'image étant parallèle, on a $\color{red}{\gamma \ = \ \dfrac{A'B'}{AB} \ = \ \dfrac{OA'}{OA}}$ (théorème de Thalès)
C34. Modèle de l'œil.
$\bullet$ La lumière entre dans l'œil par la pupille faisant office de diaphragme.
$\bullet$ Elle passe ensuite par le cristallin faisant office de lentille convergente.
$\bullet$ L'image se forme alors sur la rétine faisant office d'écran.
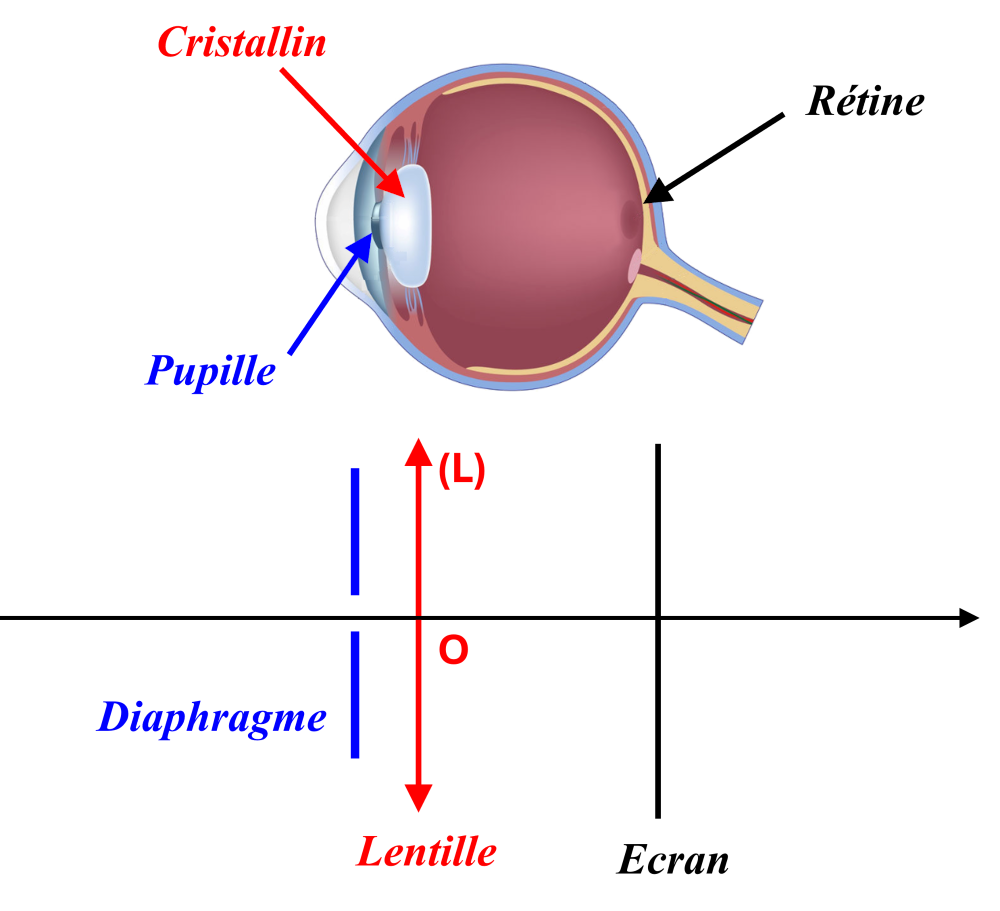
Ajouter un commentaire