1 PCPE Thermo

Exercice n°15 P409 : Contributions microscopiques.

1a,b.

L'énergie interne d'un gaz est constituée des énergies cinétiques microscopiques correspondant à l'agitation thermique et des énergies potentielles d'interaction entre les molécules.

2a,b.

Les molécules se déplacent plus ou moins, en fonction de la température.

3a,b.

Les interactions entre molécules sont dues aux interactions électrostatiques. Pour l'air, les molécules sont suffisamment éloignes les unes des autres pour ne pas les considérer.

Exercice n°16 P409 : Qui a le plus d'énergie ?

1.

Pour l'eau liquide, l'énergie potentielle de pesanteur. Pour l'eau à l'état gazeux, c'est l'énergie cinétique d'agitation.

2. 

Le système gazeux possède la plus grande énergie interne.

Exercice n°18 P409 : Chocolat fouetté.

1.

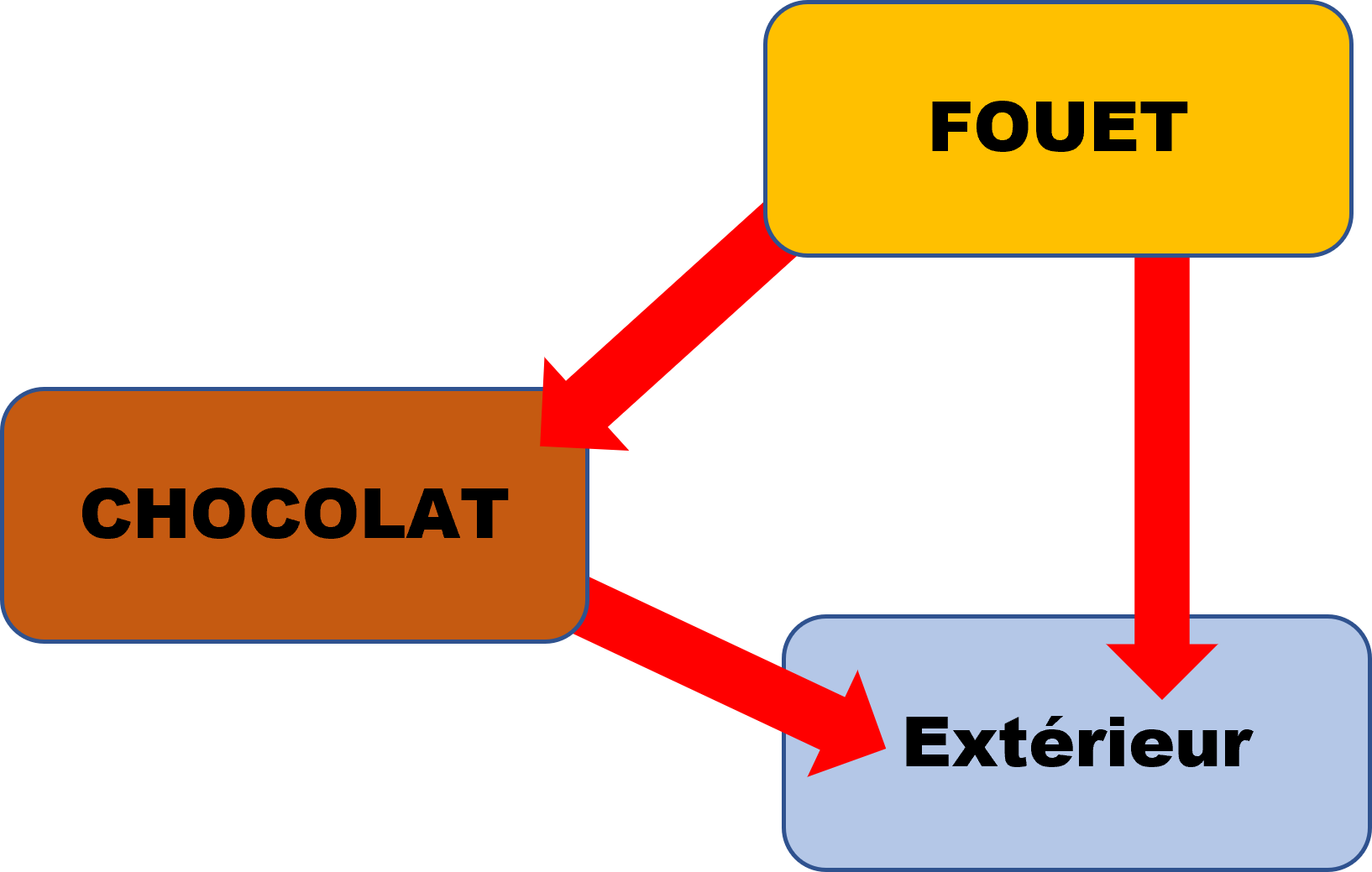
2 a,b.

Le système "chocolat" ne se déplace pas. Il est au repos. Le premier principe de la thermodynamique s'écrit : $\Delta U \ = \ Q + W$, où $W$ est le travail des forces fourni par le fouet et $Q$ le transfert thermique.

2c.

$\Delta U \ = \ 10 \ - 50 \ = -40 \ kJ$.

Exercice n°19 P409 : Pompe à chaleur.

1.

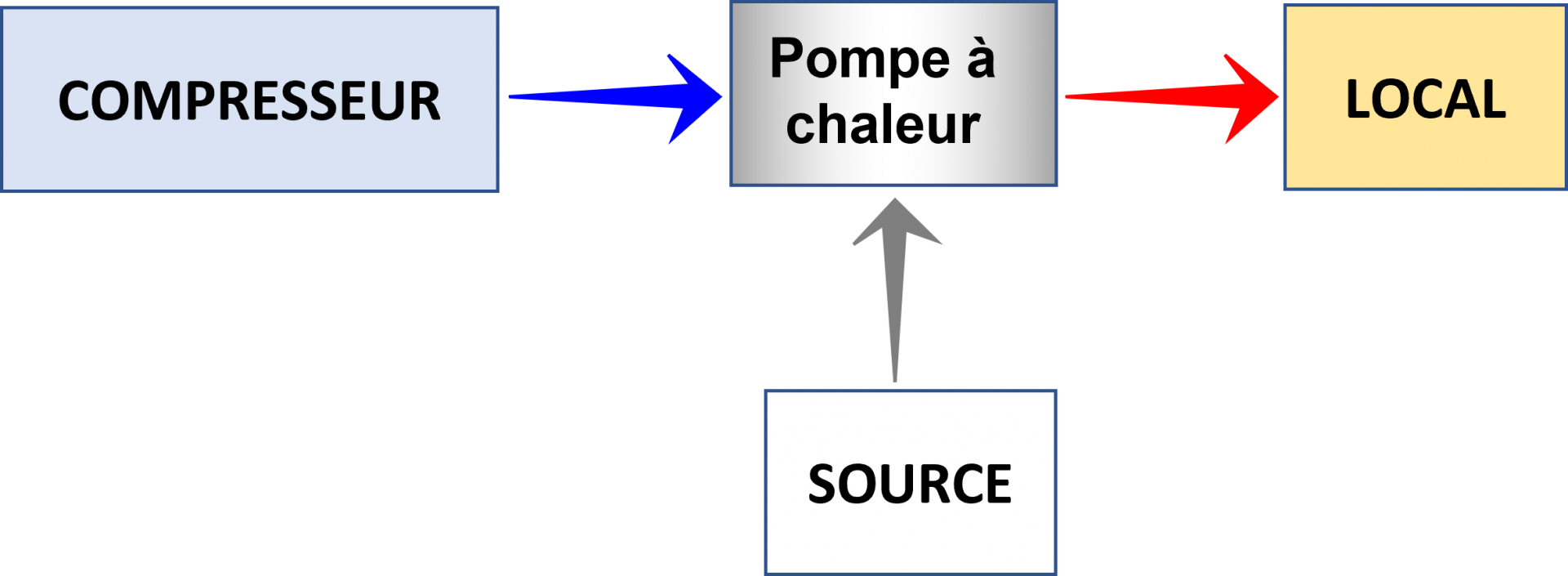
2.

$\Delta U_{ \ pompe} \ = \ Q_{ \ source} \ + \ W_{compresseur} \ + \ Q_{ \ local} $

NB : $Q_{ \ source} \ > \ 0 \ , \ W_{compresseur} \ > 0 \ , \ Q_{ \ local} \ < \ 0$

Exercice n°20 P410 : Pertes thermiques d'une habitation.

1.

$\Delta \ U \ = \ Q \ = \ m_{air} \times c_{air} \times \Delta \ T \ = \ - 1000 \times c_{air} \times \left ( T_2 \ - \ T_1 \right )$

$\Delta \ U \ = \ Q \ = \ \rho_{air} \times V \times c_{air} \times \Delta \ T \ = \ 1,3 \times 400 \times 1000 \times \left ( 15,6 \ - \ 19 \right ) \ = \ -1768.10^{ \ 3} \ J$

2.

Cette valeur est négative : le système {air} cède de l'énergie à lextérieur.

Exercice n°21 P410 : Mug de thé au micro-ondes.

1.

$\Delta \ U_{eau} \ = \ m \times c \times \Delta T \ = \ 0,250 \times 4180 \ 80 \ = \ 8,36.10^{ \ 4} \ J$

2.

Cette variation d'énergie correspond à celle fournie par le four :

$E \ = \ P \times \Delta \ t \ = \ \Delta \ U$ soit : $\Delta \ t \ = \ \dfrac{\Delta \ U}{P} \ = \ \dfrac{8,36.10^{ \ 4}}{900} \ = \ 93 \ s$

Exercice n°25 P410 : Bon choix d'isolant.

1a.

Le transfert thermique s'effectue des pièces sous le grenier vers celui-ci.

1b.

L'expression du flux thermique est : $\Phi \ = \ \dfrac{T_C-T_F}{R_{Th}}$ où $R_{Th} \ = \ \dfrac{e}{\lambda \times S}$ représente la résistance thermique.

Ici : $\Phi \ = \ \dfrac{20 \ - \ 5}{7,5.10^{ \ -3}} \ = \ 2000 \ W$

2a.

Pour diminuer le flux $\Phi$, il faut augmenter la résistance thermique $R_{Th}$ et donc, diminuer la conductivité thermique $\lambda$. Parmi les matériaux proposés, on choisira le polystyrène extrudé.

2b,c.

Pour diviser le flux $\Phi$ par 10, il faut multiplier la résistance thermique $R_{Th}$ par 10. La résistance totale sera :

$R_{Totale} \ = \ 10 \times R \ = \ R_{sol} \ + \ R_{isolant}$

$10 \times R \ = \ R_{sol} \ + \ \dfrac{e}{\lambda \times S}$

$ e \ = \ 9 \times R \times \lambda \times S \ = 9 \times 7,5.10^{ \ -3} \times 3,3.10^{ \ -2} \times 80 \ = \ 18.10^{ \ -2} \ m$

Exercice n°27 P411 : Loi de Stefan Boltzmann.

1.

En considérant la Terre comme un corps noir, elle émettra totalement sous forme de rayonnement l'énergie reçue du Soleil.

2a.

$F \ = \ \sigma \ T^{ \ 4} \ \Leftrightarrow \ \sigma \ = \ \dfrac{F}{T^{ \ 4}}$

$ \sigma$ s'exprime donc en $W.m^{ \ -2}.K ^{ \ -4}$

2b.

$ T \ = \ \left (\dfrac{F}{\sigma} \right )^{ \ 1/4} \ = \ \left (\dfrac{342}{5,67.10^{ \ -8}} \right )^{ \ 1/4} \ = \ 278,7 \ K $ soit : 5,5°C

3.

La valeur obtenue est inférieure à la valeur réelle car une partie des rayonnements émis sont renvoyés par la couche atmosphérique.

Exercice n°28 P411 : Refroidissement d'une tasse de café.

1.

La tasse de café cède de la chaleur au milieu extérieur.

2.

$T_{amb} \ = \ 25°C$.

3.

$\dfrac{dT(t)}{dt} \ = \ \gamma \times \left (T(t) \ - \ T_{amb} \right )$.

Il s'agit d'une équation différentielle du premier ordre. La solution générale est $T(t) \ = \ A \times e^{ \ - \gamma \times t} \ + \ B$

A l'instant $t \ = \ 0$, la tasse est à la température $T(0) \ = \ A \times e^{ \ - \gamma \times 0} \ + \ B \ = \ 75$ donc : $T(0) \ = \ A \ + \ B = \ 75$

A l'instant $t \ = \ + \infty $, la tasse sera à la température de la pièce $T(\infty) \ = \ A \times e^{ \ - \gamma \times \infty} \ + \ B \ = \ 25$ donc : $T(0) \ = \ B = \ 75$

On en déduit : $ \ \ \ \fbox{$T(t) \ = \ 50 \ \times e^{ \ - \gamma \times t} \ + \ 25 \ \ \ $}$

4a.

A l'instant $t \ = \ 300 \ s$, la tasse est à la température $T(300) \ = \ 50$.

Soit : $50 \times e^{ \ - \gamma \times 300} \ + \ 25 \ = \ 50$.

$\Leftrightarrow \ e^{ \ - \gamma \times 300} \ = \ \dfrac{50-25}{50} \ = \ \dfrac{1}{2}$.

$\Leftrightarrow \ - \ 300 \times \gamma \ = \ ln \left ( \dfrac{1}{2} \right )$.

$\Leftrightarrow \ \gamma \ = \ \dfrac{ln(2)}{300} \ = \ 2,3.10^{ \ -3} \ K^{ \ -1}$.

4b.

On en déduit : $\fbox{$ \ \ \ T(t) \ = \ 50 \ \times e^{ \ - 2,3.10^{ \ -3} \times t} \ + \ 25 \ \ \ $}$