Activités Acide/Base Tale
Correction
Activité 1 :
A11 :
La définition de Boyle se base uniquement sur les observations, ne faisant intervenir aucune espèce chimique particulière.
A12 :
$HNO_3 \longrightarrow H^+ + NO_3^{\ - } $
$Ca \left( OH \right ) _{2(s)} \longrightarrow Ca^{2+} + 2 \ HO^{ \ -}$
A13 :
Elle repose sur deux espèces.
A14 :
La définition des acides est la même, seule celle des bases diffère.
A15 :
$C_6H_8O_6 \longrightarrow C_6H_7O_6^{ \ - } + H^{ \ +} $
$ CO_3^{ \ 2-} + 2 H^{ \ +} \longrightarrow H_2CO_3$
A16 :
Elle est passée d'observations, puis a évolué en utilisant sur des expériences, faisant apparaître des espèces chimiques spécifiques.
Activité 2 :
A21. Observation n°1.
A21a :
Les réactifs sont : $HCl \ et \ NH_3. $
Ils sont tous les deux à l'état gazeux.
La réaction est : $HCl_{(g)} + NH_{3(g)} \longrightarrow NH_4Cl_{s}$
Soit : $\left ( NH_4^{ \ + } ; Cl ^{ \ - } \right ) $.
L'espèce $HCl$ a cédé un ion $H^{ \ + }$ à l'espèce $NH_3$ (qui l'a accepté).
L'acide est donc : $HCl$ et la base $NH_3$.
A21b :
Les deux couples acide/base intervenant sont : $H^{ \ + } / H_2O $ et $NH_4^{ \ +} / NH_3$
Pour le premier couple : $HCl \longrightarrow H^{ \ +} + Cl^{ \ - } $
Pour le deuxième : $NH_3 + H^{ \ + } \longrightarrow NH_4^{ \ + }$
A21c :
$HCl_{ (g)} + NH_{3(g)} \ \longrightarrow \ NH_4^{ \ +} + Cl^{ \ -}$
A22. Observation n°2.
A22a :
Les réactifs sont : $HO ^{ \ - } \ et \ NH_4^{ \ + }. $
Ils sont tous les deux à l'état liquide.
L'acide est $ NH_4^{ \ + } , la base $HO^{ \ -}$
Les deux couples acide/base intervenant sont : $NH_4^{ \ + } / NH_3$ et $H_2O / HO^{ \ - }$
Les deux réaction acide/base sont :
$NH_{4(aq)}^{ \ + } + H_2O_{(l)} \overleftarrow{\longrightarrow} NH_{3(aq)} + H_3O_{(aq)}^{ \ +}$
$HO_{(aq)}^{ \ - } + H_3O_{(aq)}^{ \ +} \overleftarrow{\longrightarrow} 2H_2O{(l)} $
La réaction globale est :
$NH_{4(aq)}^{ \ + } + HO_{(aq)}^{ \ - } \overleftarrow{\longrightarrow} NH_{3(aq)} + H_2O_{(l)}$
A22b :
L'acide du premier couple réagit avec la base du second pour former la base du premier et l'acide du premier.
A23. Synthèse.
A23a :
La réaction Acide/Base s'écrit avec une double flèche $\overleftarrow{\longrightarrow}$ car elle est réversible, pouvant avoir lieu dans un sens ou dans l'autre.
A23b :
En considérant deux couples Acide/Base : $A_1H/A_1^{ \ - } $ et $A_2H/A_2^{ \ - }$, la réaction s'écrira :
$A_1H + A_2^{ \ - } \overleftarrow{\longrightarrow} A_1^{ \ - } + A_2H$
EXERCICES
10 P 27 :
1. Selon Bronsted, un acide est une espèce qui peut céder un ion $H^{ \ + }$, une base est une espèce qui peut capter un ion $H^{ \ + }$.
2.
| Acide | $H_3PO_4$ | $H_2O$ | $ClOH$ | $H_2S$ | $HS^{ \ - } $ | $NH_4^{ \ + }$ |
| Base | $H_3PO_4^{ \ - }$ | $HO^{ \ - }$ | $ClO^{ \ - }$ | $HS^{ \ - }$ | $H_2S$ | $NH_3$ |
11 P 27 :
a) Faux. Si $H_2O_2$ était un acide, sa base conjuguée serait : $HO_2^{ \ - }$ (perte d'un ion $H^{ \ + }$ ), le couple acido basique serait alors : $H_2O_2/ HO_2^{ \ - } $. Et la demi-équation acide/base : $H_2O_2 \overleftarrow{\longrightarrow} H^{ \ + } + HO_2^{ \ - } $
b) Vrai. $H_3O_{ (aq)} \overleftarrow{\longrightarrow} H_{(aq)}^{ \ + } + H_2O_{(l)} $ (perte d'un ion $H^{ \ + }$ ).
c) Faux. En considérant $H_2O$ comme un acide, sa base conjuguée serait : $HO^{ \ - }$ (perte d'un ion $H^{ \ + }$ ), le couple acido basique serait alors : $H_2O_{(l)}/ HO^{ \ - } $. Et la demi-équation acide/base : $H_2O_{(l)} \overleftarrow{\longrightarrow} H_{(aq)}^{ \ + } + HO_{(aq)}^{ \ - } $
d) Vrai. En considérant $H_3O^{ \ +}$ comme un acide, sa base conjuguée serait : $H_2O_{ (l) }$ (perte d'un ion $H^{ \ + }$ ), le couple acido basique est donc : $H_3O_{(aq)}^{ \ +} / H_2O_{ (l) } $.
Et la demi-équation acide/base : $H_3O_{(aq)}^{ \ +} \overleftarrow{\longrightarrow} H_{(aq)}^{ \ +} + H_2O_{(l)} $
e) Faux. Voir c)
f) Vrai. Voir c)
12 P 27 : La soude
1. $NaOH_{(s)}$.
2. $NaOH_{(s)} \xrightarrow{ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }{} Na_{(aq)}^{ \ + } + HO_{(aq)} ^{ \ - }$.
3. Parmi les deux espèces ci-dessus, la base est : $ HO_{(aq)} ^{ \ - }$.
4. $ H_2O_{(l)} / HO_{(aq)} ^{ \ - }$.
15 P 27 : l'eau, une espèce amphotère.
1. $H_3O^{\ + } / H_2O_{(l)}$ et $H_2O_{(l)} / HO_{(aq)}^{ \ - } $
2. L'eau est dite "amphotère" car elle est à la fois l'acide et la base de deux couples.
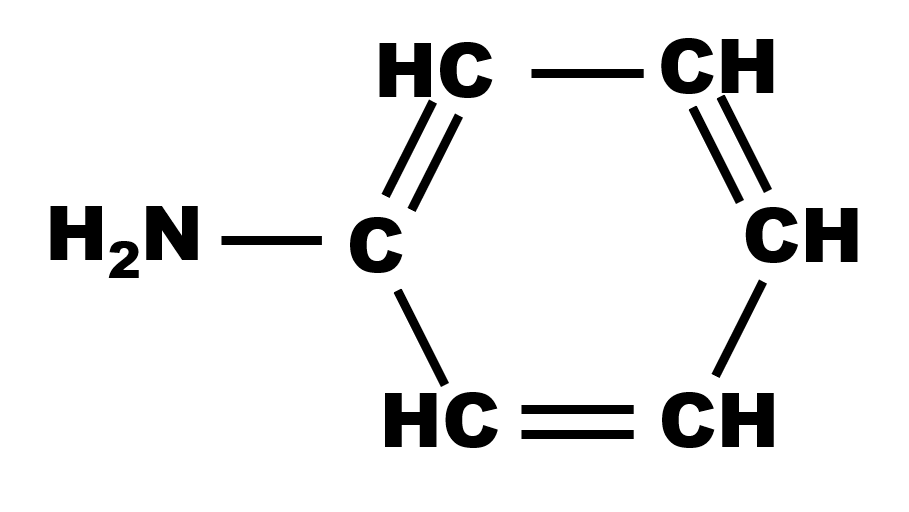
17 P 27 : l'aniline
1a,b,c.
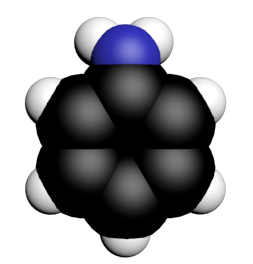 |
|
2a.
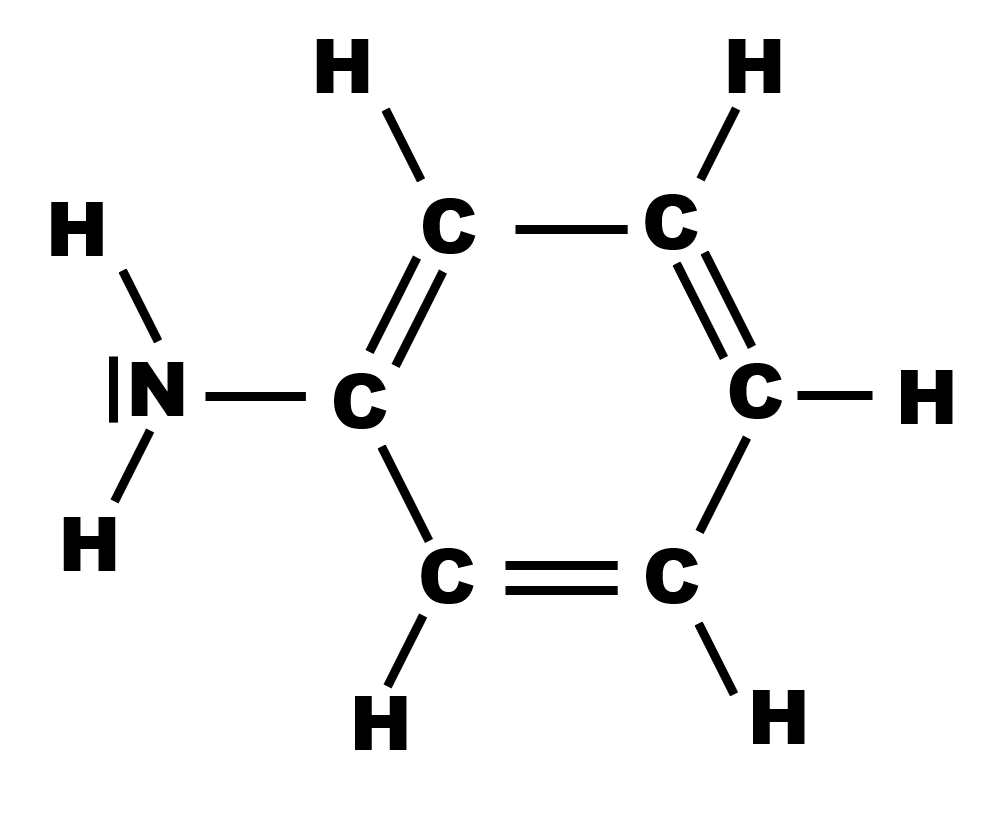
Le doublet non liant sur l'atome d'azote permet d'accepter un atome d'hydrogène. Il s'agit donc d'une base.
2b.
| Formule semi-développée. | Représentation de Lewis. |
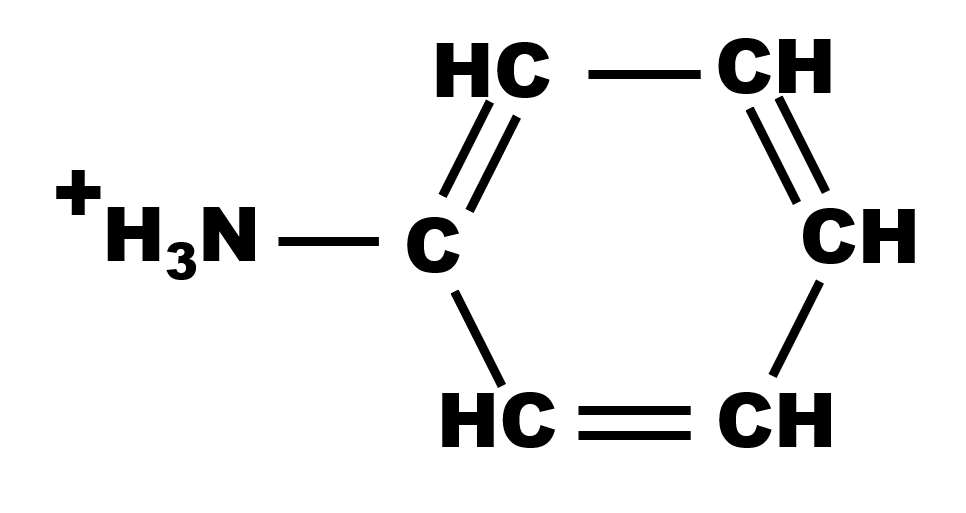 |
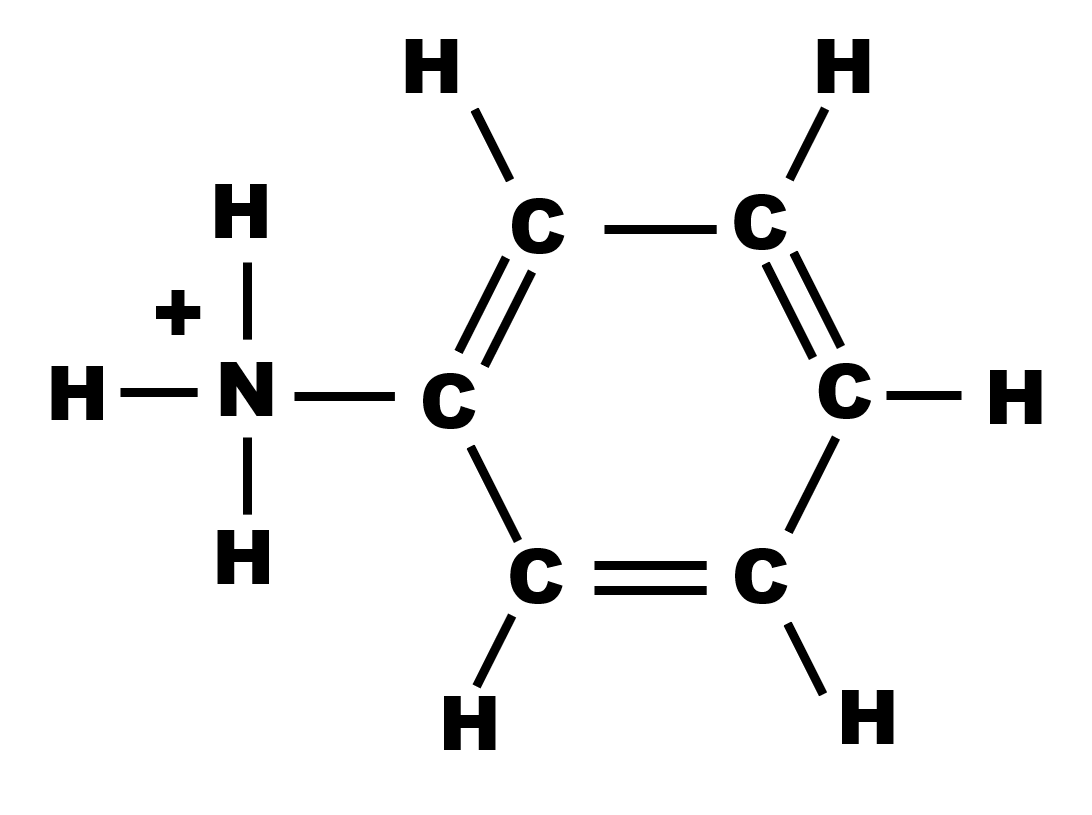 |
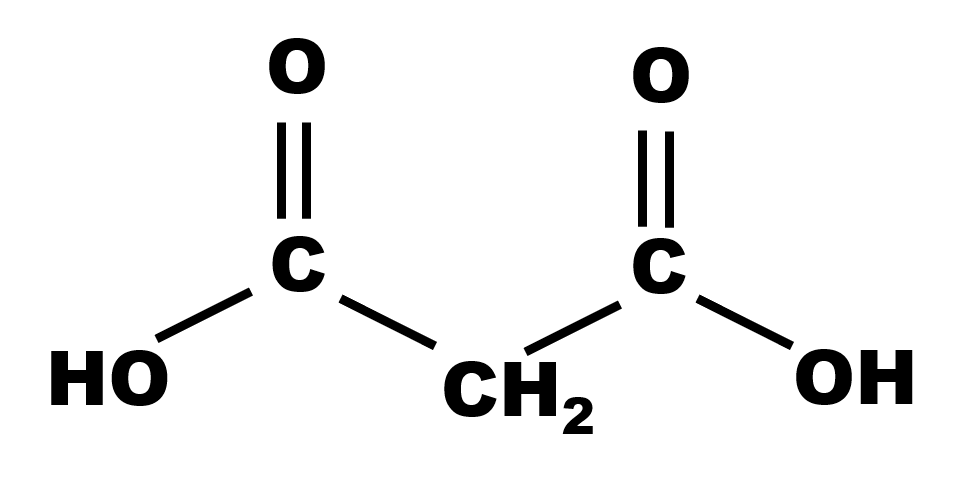
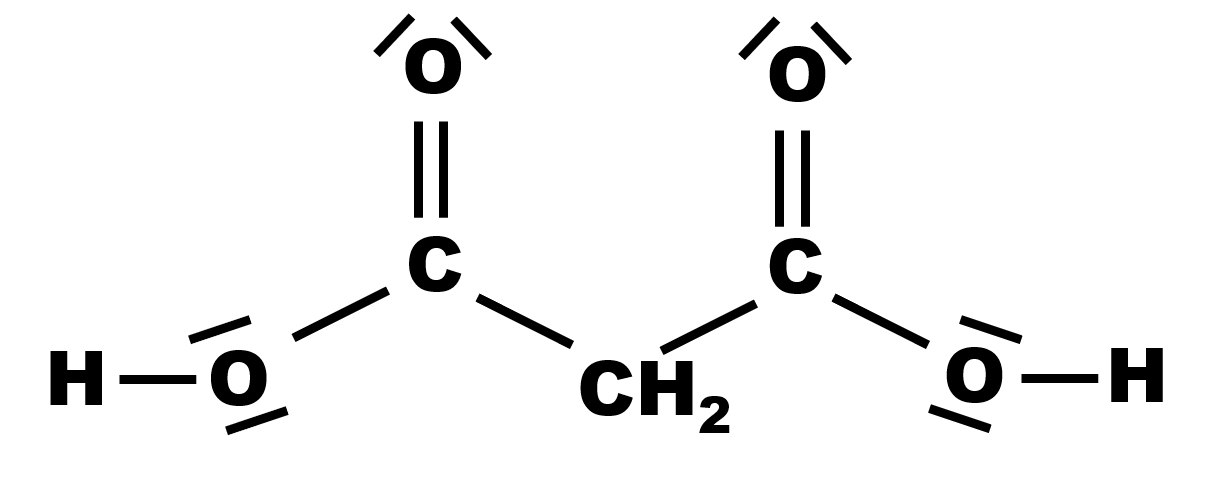
19 P 28 : L'acide malonique.
1,2,3.
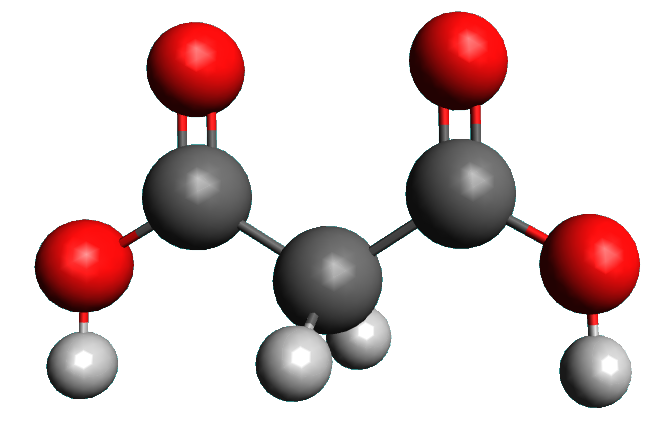 |
|
4,5.
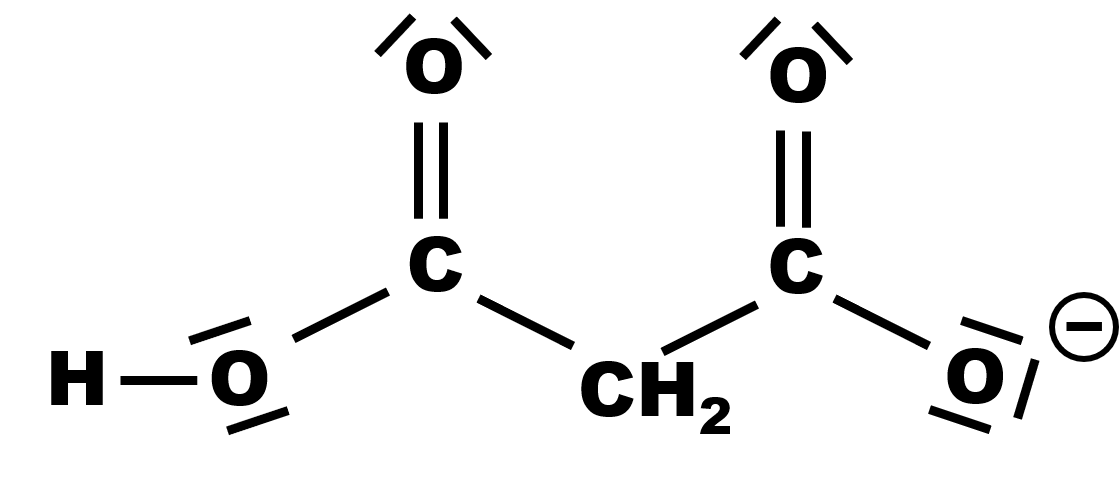 |
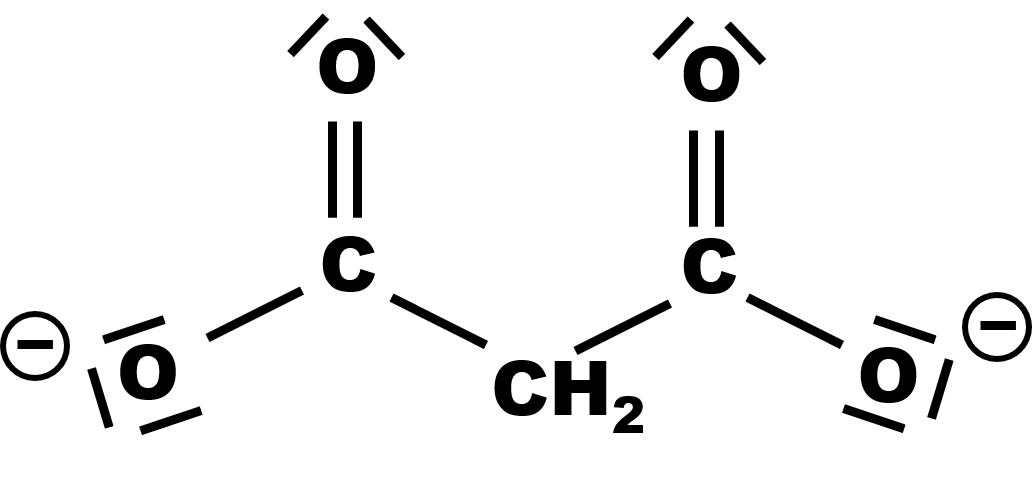 |
| ion hydrogénomalonate | ion malonate |
6.
Les deux couples acido-basiques sont : $C_2H_4O_4 /C_2H_3O_4^{ \ -} $ et $C_2H_3O_4^{ \ -} /C_2H_2O_4^{ \ 2 -} $.
L'espèce $C_2H_3O_4^{ \ -}$ est à la fois l'espèce acide d'un couple l'espèce basique d'un autre couple, c'est l'espèce amphotère.
21 P 28 : Un zwittérion
1.
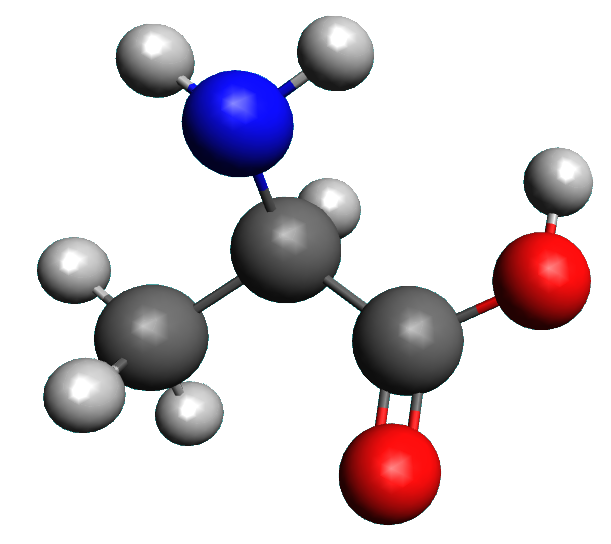 |
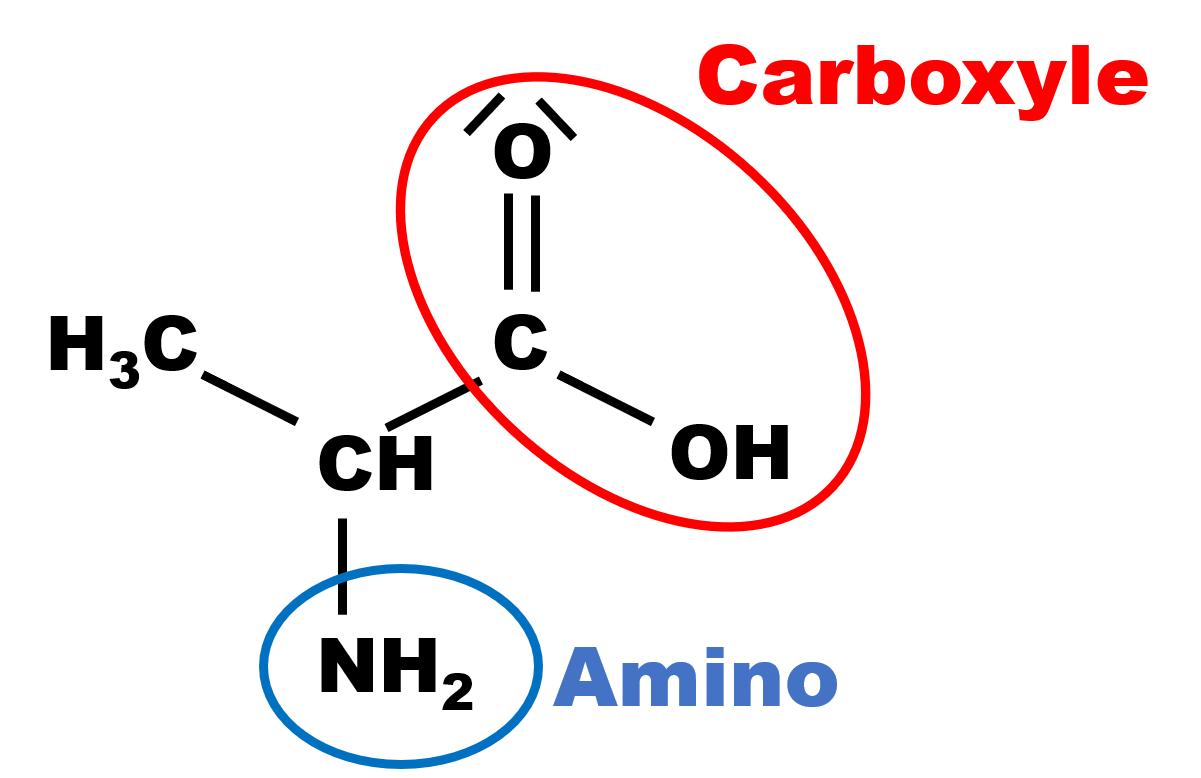 |
2.
Le groupe carboxyle est le groupe acide, le groupe amino est le groupe basique.
3.
Le groupe carboxyle, céde un ion $H^{ \ + }$ , tandis que le groupe amino, accepte un ion $H^{ \ + }$..
4.
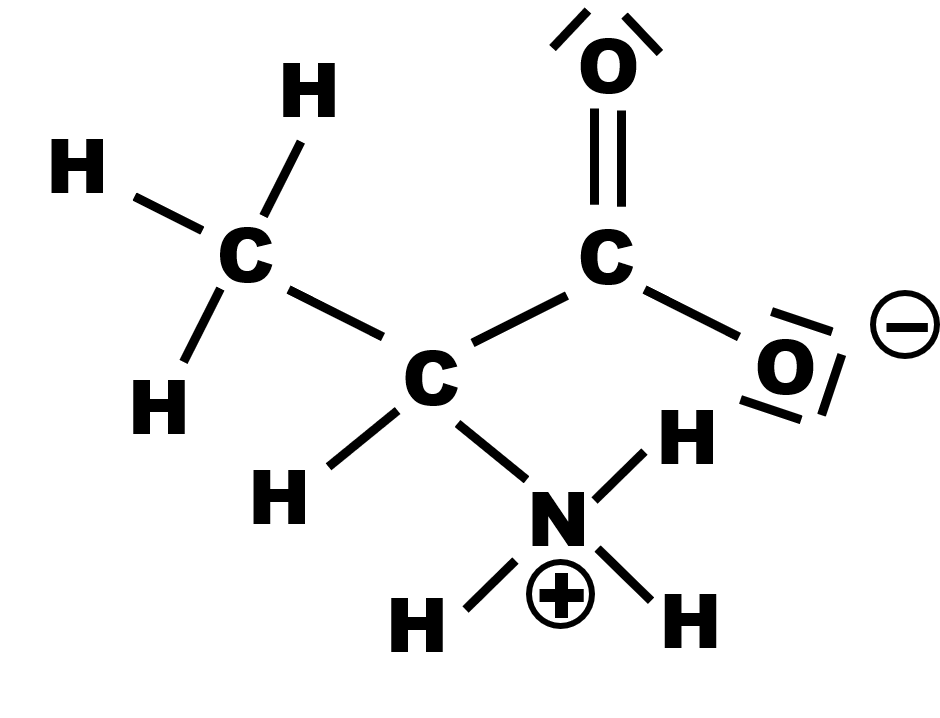
5.
|
Le site pouvant céder un ion $H^{ \ + }$ est $NH_3^{ \ + }$. La forme basique est : |
$CH_3CH\left ( NH_2 \right ) COO^{ \ - }$ |
6.
|
Le site pouvant capter un ion $H^{ \ + }$ est $COO^{ \ - }$. La forme acide est : |
$CH_3CH\left ( NH_3^{ \ + } \right ) COOH$ |
7.
Les deux couples acido-basiques sont : $CH_3CH\left ( NH_3^{ \ + } \right ) COOH / CH_3CH\left ( NH_3^{ \ + } \right ) COO^{ \ - } $ et $CH_3CH\left ( NH_3^{ \ + } \right ) COO^{ \ - } / CH_3CH\left ( NH_2\right ) COO^{ \ - }$
8.
L'ion $CH_3CH\left ( NH_3^{ \ + } \right ) COO^{ \ - } $ est à la fois l'acide d'un couple acido-basique et la base d'un autre couple.
Il s'agit d'une espèce amphotère.
23 P 28 : Des réaction acide-base.
Réaction 1.
$CH_3NH_{3(aq)}^{ \ + } + CH_3CO_{2(aq)}^{ \ - } \overleftarrow{\longrightarrow} CH_3NH_{2(aq)}+ CH_3CO_{2(aq)}H $
Réaction 2.
$H_{3}O _{(aq)}^{ \ + } + CH_3CO_{2(aq)}^{ \ -} \overleftarrow{\longrightarrow} H_{2}O_{(l)} + CH_3CO_{2(aq)}H $
Réaction 3.
$H_{2}O_{(l)} + CH_3CO_{2(aq)}^{ \ - } \overleftarrow{\longrightarrow} HO^{ \ -} + CH_3CO_{2(aq)}H $
Réaction 4.
$CH_3CO_2H_{(aq)} + CH_3NH_{2(aq)} \overleftarrow{\longrightarrow} CH_3CO_{2(aq)}^{ \ - } + CH_3NH_{3(aq)} ^{ \ + }$
Réaction 5.
$H_{3}O _{(aq)}^{ \ + } + CH_3NH_{2(aq)} \overleftarrow{\longrightarrow} H_{2}O_{(l)} + CH_3NH_{3(aq)} ^{ \ + } $
Réaction 6.
$H_{2}O_{(l)} + CH_3NH_{2(aq)} \overleftarrow{\longrightarrow} HO^{ \ -} + CH_3NH_{3(aq)} ^{ \ + } $
Réaction 7.
$CH_3CO_2H_{(aq)} + H_2O_{(l)} \overleftarrow{\longrightarrow} CH_3CO_{2(aq)}^{ \ - } + H_3O_{(aq)} ^{ \ + }$
Réaction 8.
$CH_3NH_{3(aq)}^{ \ + } + H_2O{(l)} \overleftarrow{\longrightarrow} CH_3NH_{3(aq)} ^{ \ + } + H_{3}O _{(aq)}^{ \ + } $
Réaction 9.
$ 2 \ H_{2}O_{(l)} \overleftarrow{\longrightarrow} HO^{ \ -} + H_{3}O _{(aq)}^{ \ + } $
Réaction 10.
$CH_3CO_2H_{(aq)} + HO^{ \ -} \overleftarrow{\longrightarrow} CH_3CO_{2(aq)}^{ \ - } + H_{2}O_{(l)}$
Réaction 11.
$CH_3NH_{3(aq)}^{ \ + } + HO^{ \ -} \overleftarrow{\longrightarrow} CH_3NH_{3(aq)} ^{ \ + } + H_{2}O_{(l)} $
Réaction 12.
$H_{3}O _{(aq)}^{ \ + } + HO^{ \ -} \overleftarrow{\longrightarrow} 2 \ H_{2}O_{(l)} $
24 P 28 : le phosphate d'ammonium.
1. Formule : $\left ( NH_4 \right ) _3PO_4 $
2. $\left ( NH_4 \right ) _3PO_{4(s)} \xrightarrow{ \ \ \ \ eau \ \ \ \ } 3 \ NH_{4(aq)}^{ \ + } + PO_{4(aq)} ^{ 3 \ - }$
3. L'ion ammonium $NH_4 ^{ \ + } $ étant l'acide d'un couple acido-basique, l'ion phosphate $PO_4 ^{ 3 \ - }$, la base d'un autre couple, une réaction acido-basique peut avoir lieu : $ NH_{4(aq)}^{ \ + } + PO_{4(aq)} ^{ 3 \ - } \overleftarrow{\longrightarrow} NH_{3(aq)} + HPO_{4(aq)}^{2 \ - }$
26 P 28 : les brûlures d'estomac.
1. Formule : $ NaHCO_{3(s)}$
2. Equation de dissolution dans l'eau : $ NaHCO_{3(s)} \xrightarrow{ \ \ \ \ eau \ \ \ \ } Na_{(aq)}^{ \ + } + HCO_{3(aq)} ^{ \ -}$
3. Acide chlorhydrique : $ \left ( H_3O_{(aq)}^{ \ + } ; Cl_{(aq)}^{ \ - } \right )$
4. Une réaction acide-base peut avoir lieu entre l'acide: $ H_3O_{(aq)}^{ \ + }$ et la base $ HCO_{3(aq)} ^{ \ -}$.
5. $ H_3O_{(aq)}^{ \ + } + HCO_{3(aq)} ^{ \ -} \xrightarrow{ \ \ \ \ \ \ \ \ \ } H_2O_{(l)} + CO_{2(g)},H_2O_{(l)}$
6. La réaction met en évidence la formation du gaz $CO_2$ entrainant des éructations.
7. Les deux ions chlorures $Cl^{ \ - }$ et sodium $Na^{ \ + } $ forment de chlorure de sodium $NaCl$ selon la réaction :$Na_{(aq)}^{+} + Cl_{(aq)}^{ \ - } \xrightarrow{ \ \ \ \ \ \ \ \ \ } NaCl_{(s)}$.
32 P 32 : Chimie et mauvaises odeurs.
1.
Le catabolisme est l'ensemble des réactions de dégradation des molécules par l'organisme.
La dégradation des protéines conduit à la production des amines nauséabondes et volatiles.
2a.
$HCl_{(g)} \ + \ NH3_{(g)} \ \longrightarrow \ NH_4Cl_{(s)}$
2b.
Les couples acide/base mis en jeu sont : $NH_4^{ \ +}/NH_3$ et $HCl/Cl^{ \ -}$
3a.
Les amines $R - NH_{2}$ sont des bases selon Bronsted, elles captent un ion $H^{ \ +}$.
L'acide chlorhydrique $HCl$ est un acide qui cède un ion $H^{ \ +}$.
$R - NH_{2(g)} \ + \ HCl_{(g)} \ \longrightarrow \ R - NH_3Cl(s)$
3b.
Les couples acide/base mis en jeu sont : $R-NH_{3}^{ \ +} / R-NH_2$ et $HCl/Cl^{ \ -}$.
3c.
Les mauvaises odeurs sont dues aux amines $R-NH_{2(g)}$ volatiles.
En réagissant avec l'acide chlorhydrique $HCl$, elles se trnasforment en solides ioniques inodores $R-NH_{3}Cl_{(s)}$ solides.
Les gaz ayant disparu, les mauvaises odeurs aussi.
35 P 33 : La verdunisation.
1.
Les couples acide/base mis en jeu sont : $CO_{2(aq)},H_2O_{(l)}/HCO_{3(aq)}^{ \ -}$ et $H_3O^{ \ +}_{(aq)}/H_2O_{(l)}$
La réaction s'écrit : $CO_{2(aq)},H_2O_{(l)} \ + \ H_2O_{(l)} \ \overleftarrow{\longrightarrow} \ H_3O^{ \ +}_{(aq)} \ + \ HCO_{3(aq)}^{ \ -}$
Il y a production d'ions hydronium $H_3O^{ \ +}_{(aq)}$, responsable de l'acidité. L'acidité augmente donc, induisant une diminution du pH.
2.
Les couples acide/base mis en jeu sont : $CO_{2(aq)},H_2O_{(l)}/HCO_{3(aq)}^{ \ -}$ et $HClO_{(aq)}/ClO^{ \ -}_{(aq)}$
La réaction s'écrit : $CO_{2(aq)},H_2O_{(l)} \ + \ ClO^{ \ -}_{(aq)} \ \overleftarrow{\longrightarrow} \ HClO_{(aq)} \ + \ HCO_{3(aq)}^{ \ -}$
La production d'acide hypochloreux $HClO_{(aq)}$. C'est un désinfectant plus efficace que $ClO^{ \ -}_{(aq)}$ car il possède un pouvoir bactéricide plus puissant. La dissolution du dioxyde de carbone $CO_{2,(aq)}$ est donc plus efficace.
36 P 33 : Les calculs urinaires.
1.
Les couples acide/base mis en jeu sont : $C_5H_4N_4NO_{3,(s)}/C_5H_3N_4NO_{3,(aq)}^{ \ -}$ et $H_3O^{ \ +}_{(aq)}/H_2O_{(l)}$
La réaction s'écrit : $C_5H_4N_4NO_{3,(s) \ + \ H_2O_{(l)} \ \overleftarrow{\longrightarrow} \ C_5H_3N_4NO_{3,(aq)}^{ \ -} \ + \ H_3O(aq)}^{ \ +}$
2a.
L'espèce majoritairement présente dans l'eau de Vichy est l'ion bicarbonate $HCO^{ \ -}_{3,(aq)}$.
2b.
Cette espèce appartient aux couples : $HCO^{ \ -}_{3,(aq)}/CO_{3,(aq)}^{ \ 2-}$ et $CO_{2(g)},H_2O_{(l)}/HCO^{ \ -}_{3,(aq)}$.
3a,b.
L'ion bicarbonate $HCO^{ \ -}_{3,(aq)}$ peut donc réagir en tant que base avec l'acide urique $C_5H_4N_4NO_{3,(s)}$ selon la réaction :
$HCO^{ \ -}_{3,(aq)} \ + \ C_5H_4N_4NO_{3,(s)} \ \overleftarrow{\longrightarrow} \ C_5H_3N_4NO_{3,(aq)}^{ \ -} \ + \ CO_{2(g)},H_2O_{(l)} $
Les ions $HCO^{ \ -}_{3,(aq)}$ réagissent avec l'acide urique $C_5H_4N_4NO_{3,(s)}$ solide insoluble dans l'eau, se transformant en ion $C_5H_3N_4NO_{3,(aq)}^{ \ -}$
4.
Pour un $pH = 6,8$ (proche de 7), 95% de l'acide urique est sous la forme de sa base conjuguée $C_5H_3N_4NO_{3,(aq)}^{ \ -}$.
5a.
Les couples acide/base mis en jeu sont : $C_5H_4N_4NO_{3,(s)}/C_5H_3N_4NO_{3,(aq)}^{ \ -}$ et $H_3O^{ \ +}_{(aq)}/H_2O_{(l)}$
5b.
$C_5H_3N_4NO_{3,(aq)}^{ \ -} \ + \ H^{ \ +}_{(aq)} \ \longrightarrow \ C_5H_4N_4NO_{3,(s)} \ + \ H_2O_{(l)}$
5c.
$$ \begin{array}{|c|c|c c c c c|} \hline Etat & Avc^t & C_5H_3N_4O_{3,(aq)}^{ \ -} \ \ + & H_3O^{ \ +}_{(aq)} \ & \longrightarrow & C_5H_4N_4O_{3,(aq)} \ + & H_2O_{(l)} \\ \hline \hline initial & t=0 & n_1 & n_2 & & 0 & 0 \\ \hline \hline en \ cours & t & n_1 - x & n_2 -x & & x & x \\ \hline \hline final & t_{final} & n_1 - x_f & n_2 -x_f & & x_f & x_f \\ \hline \end{array} $$
$n_2 \ = \ c_A \times V_a \ = \ 2,00.10^{ \ -2} \times 10,2.10^{ \ -3} \ = \ 2,04.10^{ \ -4} \ mol$
5d.
La réaction étant supposée totale, il n'y a plus d'ions hydronium à la fin, on a alors :
$$ \begin{array}{c c c } \left \{ \begin {array}{l} n_1 - x_f = 0 \\ n_2 -x_f =0 \end{array} \right. & \Leftrightarrow & \left \{ \begin {array}{l} x_f = n_1 = 2,04.10^{ \ -4} \ mol\\ n_2 = n_1 = 2,04.10^{ \ -4} \ mol \end{array} \right. \end{array} $$
On a donc formé $n_{acide \ urique} = \ 2,04.10^{ \ -4} \ mol$ dans les $50 \ mL$
La quantité d'acide urique dans le volume total ($ 1,5 \ L$ ) est donc : $N_{acide \ urique} \ = \ 30 \times 6,12.10^{ \ -3} \ mol$
5e.
La masse d'acide urique correspondante est : $m_{acide} \ = \ N_{acide \ urique} \times M_{acide \ urique} \ = \ 6,12.10^{ \ -3} \times \left ( 5 \times 12,0 + 4 \times 1,0 + 4 \times 14,0 + 3 \times 16,0 \right ) \ = \ 1,03 \ g$
5f.
$\left ( \dfrac{u_{m_{acide}}}{m_{acide}} \right )^2 \ = \left ( \dfrac{V_a}{V_a} \right )^2 + \left ( \dfrac{c_a}{c_a} \right )^2 $
Soit : $\dfrac{u_{m_{acide}}}{m_{acide}} \ = \ \sqrt{\left ( \dfrac{V_a}{V_a} \right )^2 + \left ( \dfrac{c_a}{c_a} \right )^2} \ = \ \sqrt{\left ( \dfrac{0,1}{10,2} \right )^2 + \left ( \dfrac{0,02}{2,00} \right )^2} \ = \ 0,014$
Alors : $u_{m_{acide}} \ = 0,014 \times 1,03 \ = 0,01 \ g$
Donc : $m_{acide} \ = \left ( 1,03 \pm 0,01 \right ) \ g$
5g.
La masse d'acide urique $m_{acide} \ = 1,03 \ g \ = 1,03.10^{ \ 3} \ mg$ est donc supérieure à la valeur $750 \ mg$.
5f.
Si l'alimentation favorise une diminution du $pH$, les ions urate se transormeront en acide urique, solide insoluble dans l'eau.
Ca va faire mal !!
40 P 36 : Eliminer le tartre.
1.
Le volume de $100 \ g$ de solution est : $V_{solution} \ = \ \dfrac{m_{solution}}{\rho_d} \ = \ \dfrac{100}{1,04.10^3} \ = \ 9,62.10^{ \ -2} \ L$
La quantité de matière en $HCl_{(g)}$ est $n_{HCl} \ = \ dfrac{m_{HCl}}{M_{HCl}} \ = \ \dfrac{9,0}{36,5} \ = \ 2,5.10^{ \ -1} \ mol$
La concentration est donc : $c \ = \ \dfrac{n_{HCl}}{V_{solution}} \ = \dfrac{2,5.10^{ \ -1}}{9,62.10^{ \ -2}} \ = \ 2,6 \ mol.L^{ \ -1}$
2a.
Dans la réaction $ 2 \ H_3O^{ \ +}_{(aq)} \ + \ CaCO_{3,(s)} \ \longrightarrow \ Ca_{(aq)}^{ \ 2+} \ + \ CO_{2,(g)} \ + \ H_2O_{(l)}$, l'ion $CO_3^{ \ 2-}$ capte deux ions hydronium $H_3O^{ \ +}_{(aq)}$.
Les couples acide/base sont donc : $ H_3O^{ \ +}_{(aq)}/H_2O_{(l)}$ et $CO_{2(g)} / CO_{3,(aq)}^{ \ 2-}$.
2b.
La concentration dans la solution dosée est : $c \ = \ \dfrac{n}{V} \ = \dfrac{1,2.10^{ \ -3}}{10.10^{ \ -3}} \ = \ 1,2.10^{ \ -1} \ mol.L^{ \ -1}$
La solution ayant été diluée 20 fois, la concentration de la solution commerciale est : $c_{com} \ = \ 20 \times c \ = 2,4 \ mol.L^{ \ -1}$, ce qui semble cohérent avec la valeur caluclée précédemment.
L'écart relatif correspondant vaut : $\dfrac{2,6-2,4}{2,6} \ = \ 7,7.10^{ \ -2}$, soit un pourcentage d'erreur de $7,7%$. Cette valeur est supérieur à $5 \ %$, ce qui semble assez important, mais toutefois cohérent avec la valeur attendue.
Problème à résoudre.
$\bullet$ Quantité de matière en tarte :
Le volume de tarte à dissoudre est : $V_{tartre} \ = \ \mathscr {A} \times e \ = \left ( 2 \pi R^2 + 2 \pi R.h \right ) \times e \ = \ \left ( 2 \pi (40.10^{ \ -2 })^2 + 2 \pi \times 40.10^{ \ -2 } \times 40.10^{ \ -2 } \right ) \times 10.10^{ \ -6} \ = \ 2,01.10^{ \ -5} \ m^3$
La masse correspondante est : $ m_{tartre} \ = \ \rho_{CaCO_3} \times V_{tartre} \ = \ 2,65.10^{6} \times 2,01.10^{ \-5} \ = \ 53,3 \ g$
Soit une quantité de matière : $ n_{tartre} \ = \ \dfrac{m_{tartre}}{M_{tartre}} \ = \ \dfrac{53,3}{100,1} \ = \ 5,3.10^{ \ -1} \ mol$
$\bullet$ Quantité de matière en acide :
$n_{acide} \ = \ c \times V \ = 2,6 \times 750.10^{ \ -3} \ = 2,0 \ mol$
$\bullet$ Conclusion :
La réaction se faisant mole à mole, il y a assez d'acide pour effectuer un détartrage complet.
<42 P 37 : Formule brute d'une amine.
1.
Les couples acide/base sont : $ H_3O^{ \ +}_{(aq)}/H_2O_{(l)}$ et $R-NH_{3,(aq)}^{ \ +} / R-NH_{(2,(l)}$.
2.
$ \begin{array}{|c|c|c c c c c|} \hline Etat & Avc^t & R-NH_{2,(aq)} \ \ + & H_3O^{ \ +}_{(aq)} \ & \longrightarrow & R-NH_{3,(aq)}^{ \ +} \ + & H_2O_{(l)} \\ \hline \hline initial & t=0 & n_b & n_a & & 0 & 0 \\ \hline \hline instant t & t & n_b - x & n_a -x & & x & x \\ \hline \hline final & t_{final} & n_b - x_f & n_a -x_f & & x_f & x_f \\ \hline \end{array} $
$ \begin{array}{c c c } \left \{ \begin {array}{l} n_a - x_f = 0 \\ n_b -x_f =0 \end{array} \right. & \Leftrightarrow & \left \{ \begin {array}{l} x_f = n_a \ mol\\ n_2 = x_f = n_a \ mol \end{array} \right. \end{array} $
La quantité de matière initiale en acide est : $n_a \ = \ c_a \times v_a \ = \ 0,50 \times 20,0.10^{ \ -3} \ = 10,0.10^{ \ -3} \ mol$
On a donc : $\color{red}{\boxed{x_f \ = \ 10.10^{ \ -3} \ mol}}$
3.
La quantité de matière en amine introduite est donc $x_f \ = \ 10,.10^{ \ -3} \ mol$
Considérant $n$ le nombre d'atomes de carbone présent dans l'amine, le radical $R-$ de l'amine peut s'écrire : $C_nH_{2n+1}$
La formule brute de l'amine peut s'écrire : $C_nH_{2n+1}-NH_2$.
Sa masse molaire est donc : $M_{amine} \ = \ 12,0 \times n + 1,0 \times \left ( 2n+1 \right ) + 14,0 \times 1 + 1,0 \times 2 \ = 12n + 2n+1+14+2 \ = \ 14n + 17$
4.
Pour une masse $m_{amine}$, la quantité de matière en amine est : $n_b \ = \dfrac{m_{amine}}{M_{amine}}$.
Donc : $M_{amine} \ = \ \dfrac{m_{amine}}{n_{amine}} \ = \ \dfrac{0,59}{10.10^{ \ -3}} \ = \ 59 \ g.mol^{ \ -1}$
On a alors : $14n+17 \ = \ 59$ soit : $n \ = \ \dfrac{59-17}{14} \ = \ 3$
Sa formule brute est : $C_3H_7 - NH_2$
4.
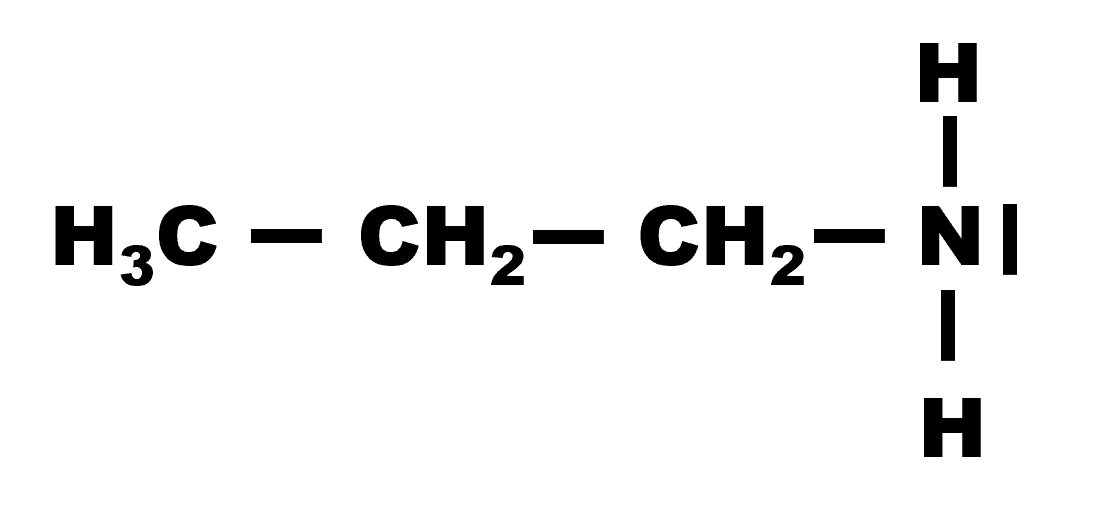 |
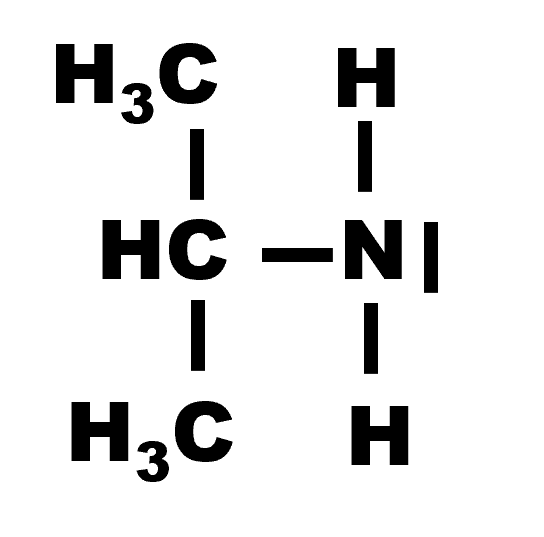 |
| Propanamine | Propan-2-amine |
5.
Les couples acide/base correpondant sont :
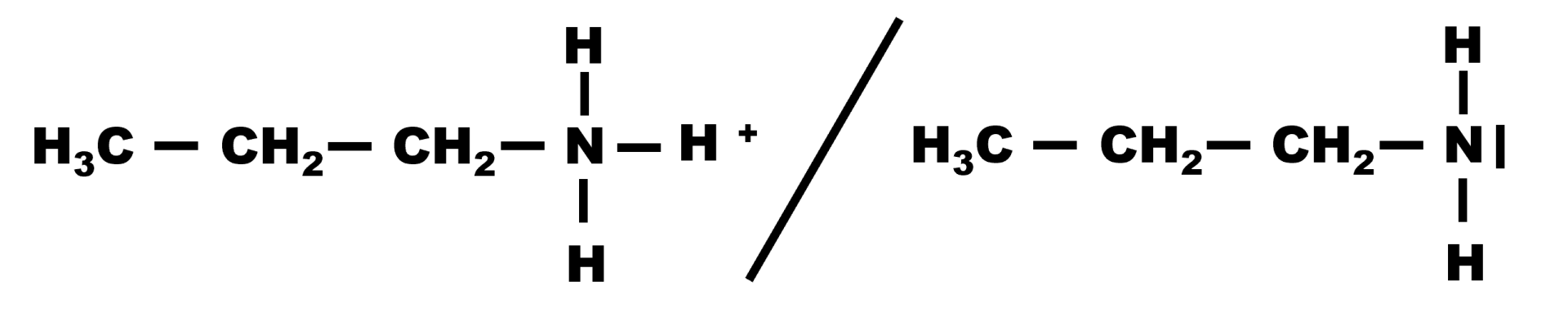
et :
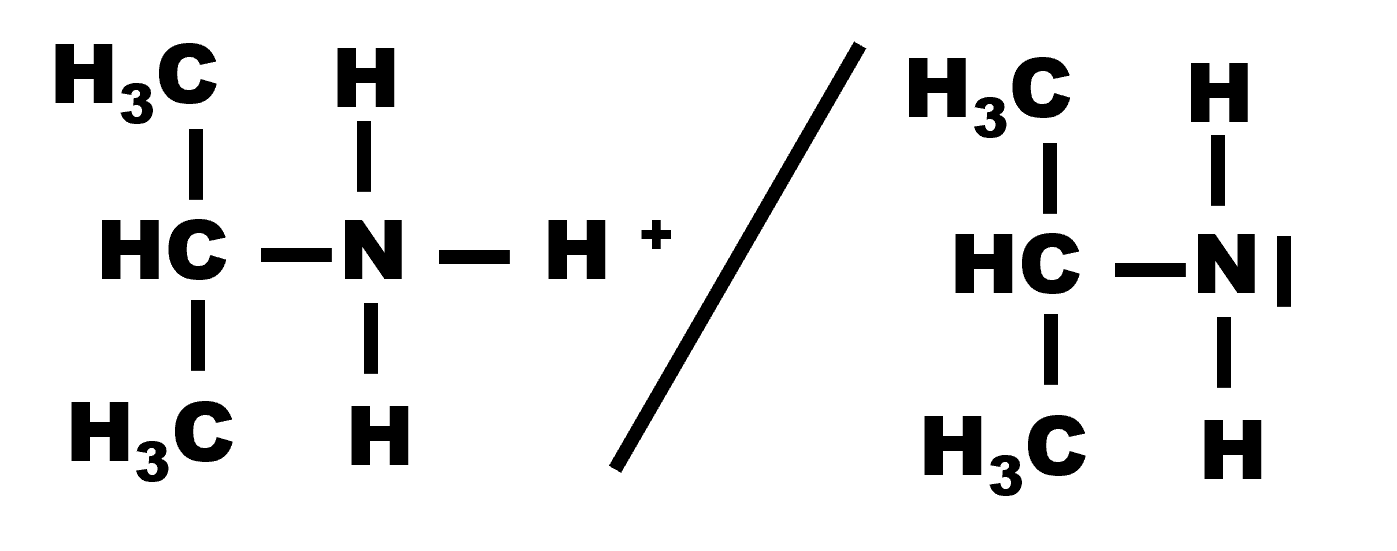
Ajouter un commentaire