Champ Uniforme

9 P 303 : Cas d'une chute verticale.

1. La seule force qui s'exerce sur la bille est son poids : $\overrightarrow P \ = m \times \overrightarrow g $.

D'après la deuxième loi de Newton : $\Sigma \overrightarrow {F_{ext}} \ = \ m \times \overrightarrow a$.

Soit :$ m \times \overrightarrow g \ = \  m \times \overrightarrow a $

Donc : $\fbox{ $\overrightarrow a \ = \ \overrightarrow g$}$

2. Alors $a(t) = g$. 

La vitesse est alors : $v_z(t) \ = \ g \times t + k $

A l'instant initial $ (t \ = \ 0)$, la bille a une vitesse nulle : $v_z(0) = 0 = \ g \times t + k_1$

On en déduit que : $k_1 \ = \ 0$ et : $\fbox {$v_z(t) \ = \ g \times t$}  $

La position en $z$ est donc :  $z(0)  \ = \ 0 \ = \dfrac{1}{2}g \times 0^2 \ + \ k_2$.

A l'instant initial, $z(0)  \ = \ 0 \ = \dfrac{1}{2}g \times 0^2 \ + \ k_2$.

On en déduit que : $k_2 \ = \ 0$ et : $\fbox {$z(t) \ = \ \dfrac{1}{2} g \times t^2$}  $.

3. La position ne variant qu'en $z$, le mouvement est rectiligne.

4. La bille atteindra le sol pour $z(t_{sol}) \ = h$. Soit : $\dfrac{1}{2}gt_{sol}^2 \ = \ h$

On en déduit : $t_{sol} \ = \ \sqrt {\dfrac{2h}{g}} $

Application numérique : $\fbox{$t_{sol} \ = \ \sqrt {\dfrac{2 \times 1}{9,81}}  \ = \ 0,45 \ s$}$.

5. Sa vitesse est alors : $v_z(t_{sol}) \ = \ g \times \sqrt {\dfrac{2h}{g}} \ = \ \sqrt {2gh}$

Application numérique : $\fbox{$v_{sol} \ = \ \sqrt {2 \times 9,81 \times 1}  \ = \ 4,43 \ m.s^{ \ -1}$}$.

10 P 303 : Cas d'un lancer oblique.

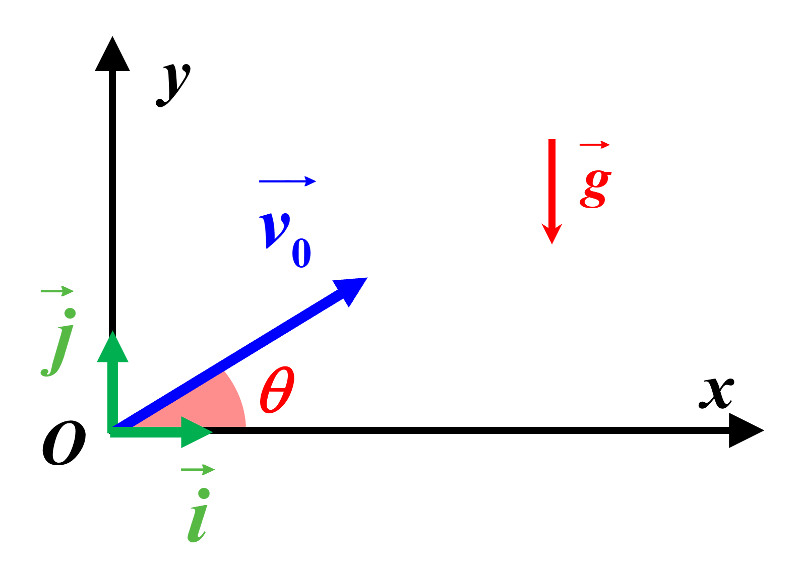
1. En négligeant les forces de frottements, la seule force qui s'exerce sur la balleest son poids : $\overrightarrow P \ = m \times \overrightarrow g $. En appliquant la deuxième loi de Newton : 

$\Sigma \overrightarrow {F_{ext}} \ = \ m \times \overrightarrow a$.

Soit :$ m \times \overrightarrow g \ = \  m \times \overrightarrow a $

Donc : $\fbox{ $\overrightarrow a \ = \ \overrightarrow g$}$.

$\overrightarrow a \ = \
\begin{pmatrix}
a_x (t) = 0 \\
a_y(t) = -g
\end{pmatrix}
$

Comme : $\overrightarrow a \ = \ \dfrac {d \overrightarrow v}{dt} $ :

$\overrightarrow {v(t)} \ = \ \begin{pmatrix} v_x (t) = k_1 \\ v_y(t) = -gt + k_2 \end{pmatrix} $
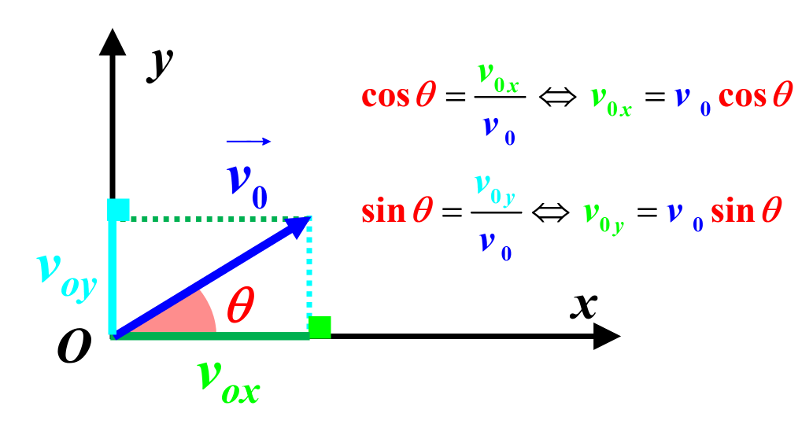
A l'instant $t=0$, le vecteur vitesse a pour coordonnées : $\overrightarrow {v(t=0)} \ = \ \begin{pmatrix} v_x (t=0) = v_{0x} = v_0.cos(\theta) \\ v_y(t=0) = v_{0y} = v_0.sin(\theta)  \end{pmatrix} $ Donc : \begin{pmatrix} v_x (t=0)=v_0.cos(\theta) = k_1 \\ v_y(t=0) =  v_0.sin(\theta) = -g \times 0 + k_2 \end{pmatrix} Soit :  $  k_1= v_0.cos(\theta) $ et $k_2 = v_0.sin(\theta)$	$\fbox{ $\overrightarrow v(t) \ = \ \ \begin{pmatrix} v_x (t) = v_0.cos(\theta) \\ v_y(t) = -g \times t + v_0.sin(\theta)  \end{pmatrix}$}$

Comme : $\overrightarrow v \ = \ \dfrac {d \overrightarrow {OM(t)}}{dt} $ :

2.

Le vecteur $\overrightarrow {OM(t)}$ n'ayant que deux composantes en $x$ et en $y$, le mouvement est plan.

3.

D'après les equations horaires de la position, on peut écrire que : $t \ = \ \dfrac{x}{v_0.cos \theta}$.

En reportant dans l'équation en $y$, on obtient : $y(x) \ = \  - \ \dfrac{1}{2}g \left ({\dfrac{x}{v_0.cos \theta}} \right )^2+v_0.sin \theta \times \dfrac{x}{v_0.cos \theta}$.

La balle touche le sol pour $y \ = \ 0$.

Soit :$ - \dfrac{1}{2}g \left ({\dfrac{x}{v_0.cos \theta}} \right )^2+v_0.sin \theta \times \dfrac{x}{v_0.cos \theta} = 0$

$\Leftrightarrow \  \ x \left ( - \  \dfrac{gx}{2 v_0^2.cos^2 \theta} + \dfrac{sin \theta}{cos \theta} \right ) \ = \ 0$

$\Leftrightarrow \   - \  \dfrac{gx}{2 v_0^2.cos^2 \theta} + \dfrac{sin \theta}{cos \theta} \ = \ 0$

$\Leftrightarrow \   - \  \dfrac{gx}{2 v_0^2.cos^2 \theta} \ = \ - \dfrac{sin \theta}{cos \theta} \ $

$\Leftrightarrow \   x \ =  \dfrac{sin \theta}{cos \theta} \times \dfrac{2v_0^2.cos^2 \theta}{g}$

$\Leftrightarrow \   x \ =  \dfrac {2v_0^2.cos \theta . sin \theta}{g}$

4.

AN : $x \ = \ \dfrac {2 \times 75^2.cos(11) . sin(11)}{9,81} \ = \ 215 \ m $.

La valeur annoncée est de 250 m. L'écart est dû aux valeurs de l'angle et de la vitesse initiaux.

11 P 303 : Aterrissage d'une perchiste.

1.

D'après la deuxièle loi de Newton : $\Sigma \overrightarrow F \ = \ m \times \overrightarrow a$.

La seule force qui s'exerce sur la perchiste pendant sa chute est sont poids $\overrightarrow P \ = m \times \overrightarrow g$.

On a donc : $\overrightarrow a = \overrightarrow g$.

Soit : $\overrightarrow a \ = \ \begin{pmatrix} a_x (t) = 0 \\ a_y(t) = 0 \\ a_z(t) = -g\\ \end{pmatrix} $

2.

Comme $ \overrightarrow a \ = \ \dfrac{d \overrightarrow {v(t)}}{dt}$ :

$\overrightarrow {v(t)} \ = \ \begin{pmatrix} v_x (t) = k_1 \\ v_y(t) = k_2 \\ v_z(t) = -g\times t + k_3\\ \end{pmatrix} $

A l'instant initial : $\overrightarrow {v(t=0)} \ = \ \begin{pmatrix} v_x (0) = v_0 \\ v_y(t) = 0 \\ v_z(t) = v_0\\ \end{pmatrix} $. Donc : $k_1 \ = \ v_0 \ , \ k_2 \ = \ 0 \ et \ k_3 \ = \ 0$.

On en déduit :

$\overrightarrow {v(t)} \ = \ \begin{pmatrix} v_x (t) = v_0 \\ v_y(t) =0 \\ v_z(t) = -g\times t \\ \end{pmatrix}$.

Comme $ \overrightarrow v \ = \ \dfrac{d \overrightarrow {OM(t)}}{dt}$ :

$\overrightarrow {OM(t)} \ = \ \begin{pmatrix} x (t) = v_0 \times t + k_4 \\ y(t) = k_5 \\ z(t) = -\dfrac {1}{2}g\times t^2 + k_6\\ \end{pmatrix} $

A l'instant initial : $\overrightarrow {OM(t=0)} \ = \ \begin{pmatrix} x (0) = 0 \\ y(0) = 0 \\ z(0) = H\\ \end{pmatrix} $.

Donc : $k_4 \ = \ 0 \ , \ k_5 \ = \ 0 \ et \ k_6 \ = \ H$.

On en déduit :

$\overrightarrow {OM(t)} \ = \ \begin{pmatrix} x (t) = v_0 \times t \\ y(t) =0 \\ z(t) = - \dfrac {1}{2} g\times t^2 +H \\ \end{pmatrix}$.

3.

La position n'ayant que deux composantes en $x$ et en $z$, le mouvement est plan.

4.

La perchiste touchera le tapis lorsque $z(t) \ = \ h$.

Soit, quand $z(t_{tapis}) = h \ \Leftrightarrow -\dfrac{1}{2}g.t_{tapis}^2 + H \ = \ h \Leftrightarrow t_{tapis} \ = \ \sqrt {\dfrac{2 (H-h)}{g}}$

AN : $t_{tapis} \ = \ \sqrt {\dfrac{2 (4,5-0,70)}{9,81}} \ = \ 0,88 \ s$

13 P 304 : Condensateur plan.

1. La direction du champ $\overrightarrow E$ est perpendiculaire aux armatures (b).

2. Lorsque la distance entre les armatures est doublée, la valeur du champ $\overrightarrow E$ est divisée par 2 (c).

3. Lorsque la tension  entre les armatures est divisé par 2, la valeur du champ $\overrightarrow E$ est doublée (b).

4. Lorsque on inverse la polarité entre les plaque, le champ $\overrightarrow E$ garde la même norme (b) et chande de sens (c).

14 P 304 : Equations horaires du mouvement d'un proton.

1.

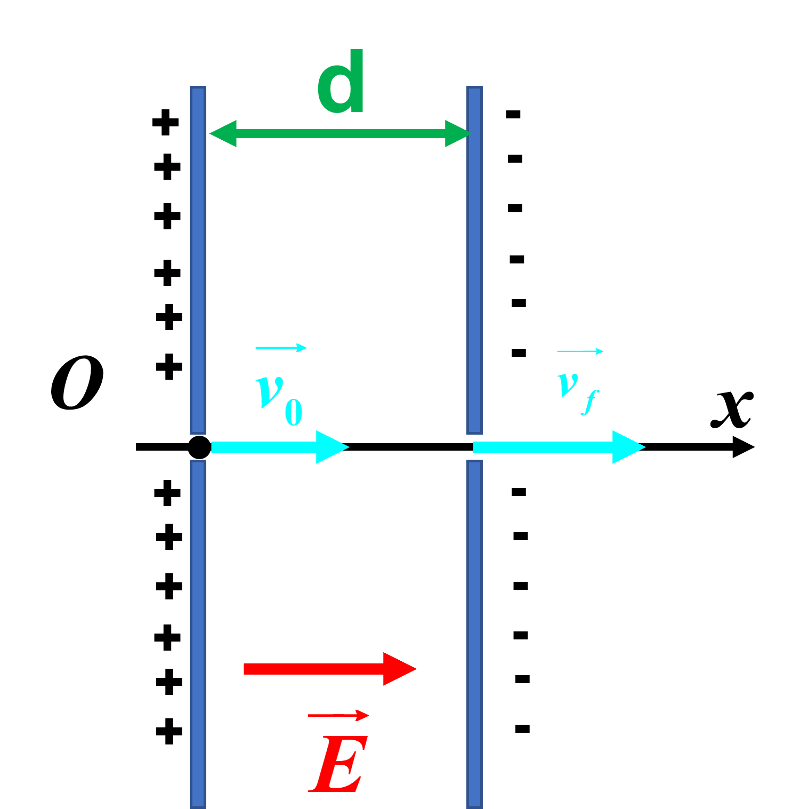Le proton, portant une charge positive : - la plaque positive du condensateur est à l'origine. - la plaque négative à l'opposé. Le champ électrique $\overrightarrow E$ étant ditigé selon les potentiels décroissants, il est dirigé comme indiqué sur la figure ci-contre.

2a.  Le rapport de la force électrostatique $F_e$ au poids $P$ est : $\dfrac {F_e}{P} \ = \ \dfrac{eE}m_pg \ = \ \dfrac{1,6.10^{ \ -19} \times 2.10^{ \ 3}}{1,7.10^{ \ -27} \times 9,81} \ = \ 1,9.10^{ \ 10 } \ >> \ 1$.

Le poids du proton peut donc être négligé devant la force électrostatique.

2b.  D'après la deuxièle loi de Newton : $\Sigma \overrightarrow F \ = \ m \times \overrightarrow a$.

Soit : $ m \times \overrightarrow a \ = \ e \times \overrightarrow E$.

Donc : $ \fbox{$ \overrightarrow a \ = \ \dfrac {e}{m} \times \overrightarrow E$}$

3a.  En projetant sur l'axe $\left ( Ox \right ) : $a_x(t) \ = \dfrac {eE}{m}$.

3b.  Comme $ \overrightarrow a \ = \ \dfrac{d \overrightarrow {v(t)}}{dt}$ :

$v_x(t) \ = \ \dfrac{eE}{m}\times t + k_1$.

A l'entrée dans le condensateur, la valeur de la vitesse est $v_0$ donc : $v_x(0) \ = \ \dfrac{eE}{m} \times 0 + k_1 \ = \ v_0$. Donc :

$ \fbox{$ v_x(t) \ = \  \dfrac {eE}{m} \times t + v_0$}$

Comme $ \overrightarrow v \ = \ \dfrac{d \overrightarrow {OM(t)}}{dt}$ :

$x(t) \ = \ \dfrac{eE}{2m}\times t^2 + v_0 \times t + k_2$.

A l'entrée dans le condensateur, la valeur de la position est $x_0$ donc : $x(0) \ = \ \dfrac{eE}{2m} \times 0^2 + v_0 \times 0 + k_2 \ = \ 0$. Donc :

$ \fbox{$ x(t) \ = \  \dfrac {eE}{2m} \times t^2 + v_0 \times t$}$

3c. Le mouvement n'a qu'une composante, il est linéaire.

4a. 

Le proton sort du condensateur quand $x(t_{sortie}) \ = \ d$.

Soit : $ \dfrac {eE}{2m} \times t_{sortie}^2 + v_0 \times t_{sortie} = d \ \Leftrightarrow \ \dfrac {e}{2m} \times t_{sortie}^2 + v_0 \times t_{sortie} - d \ = \ 0 $

$\Leftrightarrow \ = \ 1,82.10^{ \ 3 } \times t^2_{sortie} + 2,0.10^{ \ 3 } \times t_{sortie} - 18,0.10^{ \ -2} \ = \ 0$

En résolvant cette équation du second degré, on trouve : $t_{sortie} \ = \ 9,0.10^{ \ -5} \ s $

4b. 

La vitesse du proton est alors : $v_x(t_{sortie}) \ = \ \dfrac {eE}{m} \times 9,0.10^{ \ -5 } + 2,0.10^{ \ 3 } \ = \ 1,7.10 { \ 12 } \ m.s^{ \ -1 }$

La vitesse a été multipliée par : $ \dfrac{1,7.10^{ \ 12 }}{2,0.10^{3}} \ = \ 8,5.10^ { \ 8 }$.

15 P 304 : Equation de la trajectoire d'un électron.

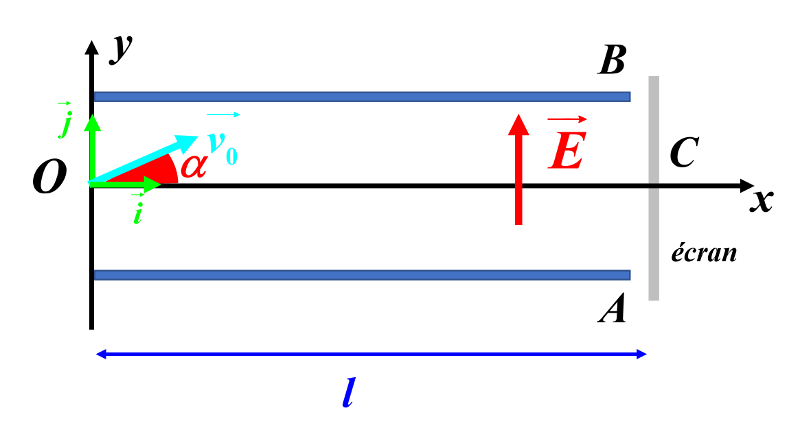
1a. Les forces auxquelles est soumis l'électron sont :

- son poids $\overrightarrow P \ = \ m \times \overrightarrow g$

- la force électrostatique $\overrightarrow F_e \ = \ -e \times \overrightarrow E$.

Cependant, le poids sera négligé. En effet : $\dfrac{F_e}{P} \ = \ \dfrac {1,6.10^{ \ -19} \times 850}{9,1.10^{ \ -31} \times 9,81} \ = \ 1,5.10^{ \ 13} \ >> \ 1$.

Ainsi, la deuxième loi de newton s'écrit : $m \times \overrightarrow a \ = \ -e \times \overrightarrow E$.

L'accélération est : $\overrightarrow a \ = \ \dfrac {-e}{m} \times \overrightarrow E$.

Dans le repère choisi : $ \fbox{$\overrightarrow a(t) \ = \ \ \begin{pmatrix} a_x(t) \ = 0 \\ a_y(t) = \dfrac {-eE}{m} \end{pmatrix}$}$

1b. Or : $\overrightarrow {a(t)} \ = \ \dfrac {d \overrightarrow v(t)}{dt}$.

On a donc : $\overrightarrow {v(t)} = \begin{pmatrix} v_x(t) \ = \ k_1 \\ v_y(t) \ = \ - \dfrac{eE}{m} \times t + k_2 \end{pmatrix}$ A l'instant initial, $t=0$, $\overrightarrow {v(0)} = \begin{pmatrix} v_x(0) \ = \ v_0.cos \alpha \\ v_y(0) \ = \ v_0.sin \alpha \end{pmatrix}$

Soit : $ k_1 \ = \ v_0.cos \alpha$ et $ - \dfrac{eE}{m} \times 0 + k_2 \ = \ v_0.sin \alpha \Leftrightarrow k_2 \ = \ v_0.sin \alpha$

Finalement : $ \fbox{$\overrightarrow v(t) \ = \ \ \begin{pmatrix} v_x(t) \ = v_0.cos \alpha \\ v_y(t) = \dfrac {-eE}{m} \times t +v_0.sin \alpha \end{pmatrix}$}$.

1c.  Comme : $\overrightarrow {v(t)} \ = \ \dfrac {d \overrightarrow {OM(t)}}{dt}$.

On a donc : $\overrightarrow {OM(t)} = \begin{pmatrix} x(t) \ = \ v_0.cos \alpha + k_3 \\ y(t) \ = \ - \dfrac{eE}{2m} \times t^2 + v_0.sin \alpha \times t + k_4 \end{pmatrix}$.

A l'instant initial, $t=0$, $\overrightarrow {OM(0)} = \begin{pmatrix} x(0) \ = \ 0 \\ y(0) \ = \ 0 \end{pmatrix}$

Soit : $ 0 \ = \ v_0.cos \alpha \times 0 + k_3 \  \  \Leftrightarrow \  \ k_3 \ = \ 0$ et $ 0 \ = \ - \dfrac{eE}{2m} \times 0^2 + v_0.sin \alpha \times 0 + k_4 \  \ \Leftrightarrow  \ \ k_4 \ = \ 0$

Finalement : $ \fbox{$\overrightarrow {OM(t)} \ = \ \ \begin{pmatrix} x(t) \ = v_0.cos \alpha \times t \\ y(t) = \dfrac {-eE}{2m} \times t^2 +v_0.sin \alpha \times t \end{pmatrix}$}$

1c. La position n'ayant que deux composantes, le mouvement est plan.

2a. En utilisant la relation $x(t) \ = \ v_0.cos \alpha \times t $ , on en déduit que : $t \ = \ \dfrac{x}{v_0.cos \alpha}$

En reportant dans l'expression de $y(t) $ : $y(x) \ = \ \dfrac {-eE}{2m} \times \left ( \dfrac{x}{v_0.cos \alpha} \right ) ^2 \ + \ v_0.sin \alpha \times \dfrac {x}{v_0.cos \alpha}$

$\fbox{$ \Leftrightarrow \ \ y(x) \ = \ \dfrac {-eE}{2m \times v_0^2cos^2 \alpha} \times x^2 \ + \ tan \alpha \times x$}$

2b. La trajectoire suivie est une parabole.

3a. Pour que l'électron arrive en C sur l'écran, il faut que : $y(l) \ = \ 0$.

$\Leftrightarrow \ \dfrac {-eE}{2mv_0^2 \times cos^2 \alpha} \times l^2 \ + \ tan \alpha \times l \ = \ 0$

$\Leftrightarrow \ l \left (\dfrac {-eE}{2mv_0^2 \times cos^2 \alpha} \times l \ + \ tan \alpha \right ) = \ 0$

$\Leftrightarrow \ \dfrac {-eE}{2mv_0^2 \times cos^2 \alpha} \times l \ + \ tan \alpha = \ 0$

$\Leftrightarrow tan \alpha = \ \dfrac {eE}{2mv_0^2 \times cos^2 \alpha} \times l $

$\Leftrightarrow 2 \times tan \alpha \times cos^2 \alpha = \ \dfrac {eEl}{mv_0^2} $

$\Leftrightarrow 2 \times \dfrac {sin \alpha}{cos \alpha} \times cos^2 \alpha = \ \dfrac {eEl}{mv_0^2} $

$\Leftrightarrow 2 \times sin \alpha \times cos \alpha = \ \dfrac {eEl}{mv_0^2}$

$\Leftrightarrow sin (2 \alpha) = \ \dfrac {eEl}{mv_0^2} $

$\fbox{$\Leftrightarrow \alpha = \ \dfrac{1}{2} Arcsin \left ( \dfrac {eEl}{mv_0^2} \right ) $}$

3b.

AN : $\alpha \ = \ \dfrac{1}{2} \times Arcsin \left ( \dfrac {1,6.10^{ \ -19} \times 850 \times 0,20}{9,1.10^{ \ -31} \times  1,0.10^{14}} \right ) \ = \ 8,7°$

18 P 305 : Accélération linéaire de particules et énergie.

1.

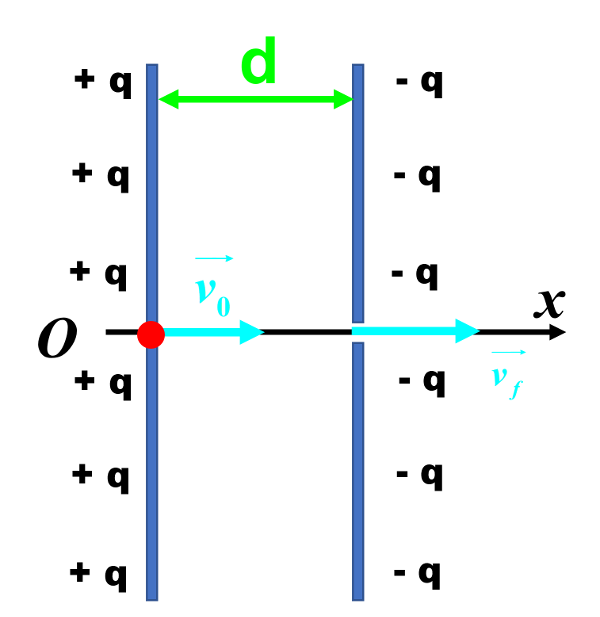La plaque du condensateur accueillant la particule à accélérer doit porter une charge du même signe que cette particule. La plaque opposée, une charge de signe opposée. La vitesse d'entrée dans le condensateur doit être dans la direction du champ électrique dans ce condensateur (orthogonal aux plaques) : - si la charge est positive : dans le même sens que le champ $\overrightarrow E$ - si la charge est négative : dans le  sens opposé à celui du champ $\overrightarrow E$

2a.

La loi de conservation de l'énergie mécanique s'écrit : $E_{c, A \ \rightarrow \ B} \ = \ E_c(B) \ - E_c(A) \ = \ -e \times U_{AB} \ = -e \times \left ( V_A \ - \ V_B \right )$

2b.

$\dfrac {1}{2} m.v_f^2 -\dfrac {1}{2} m.v_0^2 \ = \ -e \times \ U_{AB}$

$\Leftrightarrow \ \dfrac {1}{2} m.v_f^2 \ = \ -e \times \ U_{AB} + \dfrac {1}{2} m.v_0^2$

$\Leftrightarrow \  m.v_f^2 \ = 2 \times \left ( \ -e \times \ U_{AB} + \dfrac {1}{2} m.v_0^2 \right )$

$\Leftrightarrow \  v_f^2 \ = \dfrac {2 \times \left ( \ -e \times \ U_{AB}  + \dfrac {1}{2} m.v_0^2 \right )}{m}$

$\Leftrightarrow \  v_f \ = \sqrt {\dfrac {2 \times \left ( \ -e \times \ U_{AB}  + \dfrac {1}{2} m.v_0^2 \right )}{m}}$

$\Leftrightarrow \  v_f \ = \sqrt {\dfrac {2 \times \left ( \ -e \times \ U_{AB}  + \dfrac {1}{2} m.v_0^2 \right )}{m}}$

AN : $\Leftrightarrow \  v_f \ = \sqrt {\dfrac {2 \times \left ( \ -1,6.10^{ \ -19}  \times  \ (-1,0.10^{ \ 3})  + \dfrac {1}{2} 9,1.10^{ \ -31} \times (1,0.10^{ \ 3 } )^2 \right )}{9,1.10^{ \ -31}}} \ = \ 1,9.10^{ \ 7} \ m.s^{ \ -1}$

3a.

Le travail de la force électrostatique est : $W_{A,B} \ = -e \times U_{A,B} \ = -1,6.10 ^{ \ -19} \times \left (- 1,0.10^{ \ 3} \right ) \ = \ 1,6.10^{ \ -16} \ J$

3b.

Le théorème de l'énergie cinétique s'écrit : $\Delta E_c = W_{A \rightarrow B}$

Soit : $\dfrac {1}{2} m.v_f^2 -\dfrac {1}{2} m.v_0^2 \ = \ \overrightarrow F . \overrightarrow E$

$ \Leftrightarrow \ \dfrac {1}{2} m.v_f^2 -\dfrac {1}{2} m.v_0^2 \ = \ \overrightarrow F . \overrightarrow {AB}$

$ \Leftrightarrow \ \dfrac {1}{2} m.v_f^2 \ = \ -e. (-E) \overrightarrow {i} \times AB \overrightarrow {i} + \dfrac {1}{2} m.v_0^2 $

$ \Leftrightarrow \ \dfrac {1}{2} m.v_f^2 \ = \ eE \times AB + \dfrac {1}{2} m.v_0^2 $

$ \Leftrightarrow \ v_f \ = \ \sqrt { \dfrac {eE \times AB + \dfrac {1}{2} m.v_0^2}{m}} $

20 P 306 : Mouvement d'un ballon.

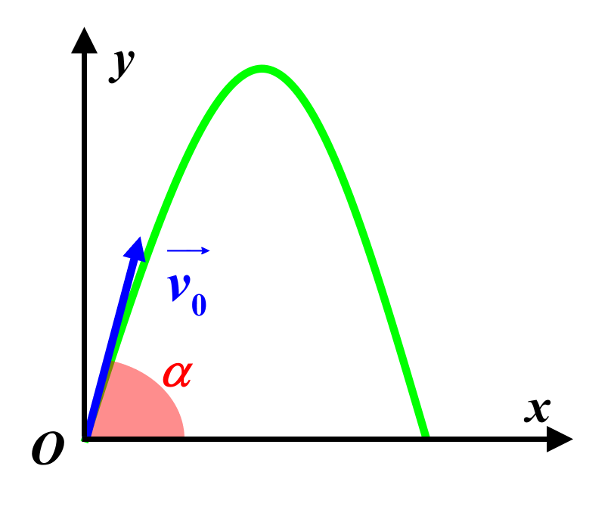
1.

En utilisant le deuxième loi de Newton (voir exercices précédents), on arrive à :

$\fbox{$\overrightarrow {OM(t)} \ = \ \begin{pmatrix} x (t) = v_0.cos(\alpha) \times t  \\ y(t) = - \dfrac {1}{2}gt^2+v_0.sin(\alpha) \times t  \end{pmatrix} $}$

2.

D'après l'équation horaire de $x(t) \ : \ t \ = \ \dfrac{x}{v_0.cos \alpha}$

En reportant dans l'équation horaire de $yx(t) $ :

$ y(x) \ = \ \dfrac{g}{2.v_0^2.cos^2 \alpha} \times x^2 \ + \ tan \alpha \times x$

3.

Le ballon touchea le sol pour $y(t) \ = \ 0$

$\Leftrightarrow \ y(t) = - \dfrac {1}{2}gt^2+v_0.sin(\alpha) \times t$

$\Leftrightarrow \ t \left ( - \dfrac {1}{2}gt+v_0.sin(\alpha) \right ) = 0$

$\Leftrightarrow \ - \dfrac {1}{2}gt+v_0.sin(\alpha) = 0$

$\Leftrightarrow \ t \ = \dfrac {2v_0.sin(\alpha)}{g}$

AN : $t \ = \dfrac {2 \times 10,0 \times sin(60)}{9,81} \ = \ 1,77 \ s$

26 P 309 : Qualité du service au tennis.

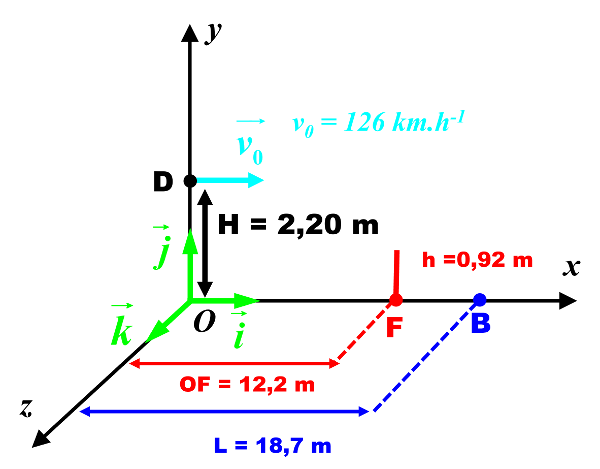
1.

De même que dans l'exercice 11, la balle n'est soumise qu'à sont poids $\overrightarrow P \ = \ m \times \overrightarrow g$.

Son accélération est : $\overrightarrow {a(t)} \ = \ \begin{pmatrix} a_x (t) = 0 \\ a_y(t) = -g \\ a_z(t) = 0 \end{pmatrix} $

2a.

On trouvera :

$\fbox{ $\overrightarrow v(t) \ = \ \ \begin{pmatrix} v_x (t) = v_0\\ v_y(t) = - g \times t \end{pmatrix}$}$

et

$\fbox{ $\overrightarrow v(t) \ = \ \ \begin{pmatrix} x (t) = v_0 \times t\\ y(t) = -\dfrac{1}{2}g \times t^2 + H \end{pmatrix}$}$

2b.

	Il s'agit d'une fonction constante de $t$. Parmi les équation temporelles déterminées précédemment, la seule correspondant est celle de $v_x(t)$
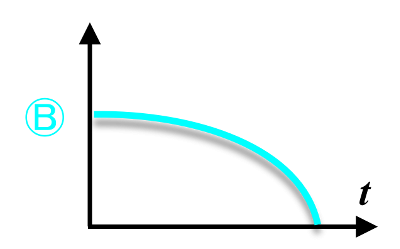	La courbe semble être une parabole de $t$. Parmi les équation temporelles déterminées précédemment, la seule correspondant est celle de $y(t)$
	Il s'agit d'une fonction linéaire de $t$ du type $ k \times t$ avec un coefficient directeur $k$ positif. Parmi les équation temporelles déterminées précédemment, la seule correspondant est celle de $x(t)$
	Il s'agit d'une fonction linéaire de $t$ du type $ k \times t$ avec un coefficient directeur $k$ négatif. Parmi les équation temporelles déterminées précédemment, la seule correspondant est celle de $v_y(t)$.

3a.

De même que dans les exercices précédents, en exprimant $t$ en fonction de $x$ : $ t \ = \ \dfrac {x}{v_0}$ et en reportant dans l'expression de $y$ en fonction de $t$, on arrive à :

$\fbox{$y(x=) \ \dfrac{-g}{2v_0^2}\times x^2 + H $}$

3b.

Pour que la balle passe au-dessus du filte, il faut que pour $x \ = \ 12,2 $ : $y \ > \ 0,92$.

$y(12,2) \ = \ \dfrac {-9,81}{2 \times \left ( \dfrac{126 \times 10^{ \ 3}}{3600} \right )^2}  \times 12,2^2+ 2,20 \  = 1,60 \ m$.

La balle passe au-dessus du filet.

3c.

Pour que le service soit valide, il faut que pour $x \ = \ 18,7 $ : $y \ < \ 0$.

$y(18,7) \ = \ \dfrac {-9,81}{2 \times  \left ( \dfrac{126 \times 10^{ \ 3}}{3600} \right )^2}  \times 18,7^2+ 2,20 \  = 0,80 \ m$.

La balle est sortie du terrain. Le service n'est pas valide.

28 P 309 : Accélérateur de particul et énergie.

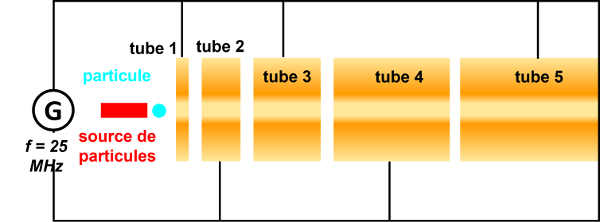
1.

Il existe une tension entre chaque cavité vide, donc un champ électrique. Chaque cavité peut être modélisée par un condensateur plan.

2a.

A la sortie d'un tube (i), la particule possède une énergie cinétique $E_{c,i}$. En traversant la cavité en sortie de ce tube, elle acquiert l'énergie potentille électrique $E_{p,él} = q.V$

En traversant le tube suivant (i+1), elle conserve cette même $E_{c,i} + E_{p,él}$ avec laquelle elle arrive en sortie de ce tube (i+1) : $E_{c,i+1) \ = \ E_{c,i} + E_{p,él}$

L'énergie potentielle $qV$ a été transférée en énergie cinétique.

2b.

$\Delta E = q.U_{AB}$

3a.

Ce gain d'énergie sera le même dans toutes les cavités à la condition que la tension entre les tubes soit la même à chaque fois que la particule traverse une cavité.

3c.

Après avoir traversé 12 cavités son gain total d'énergie sera : $\Delta E \ = \ 12 \times e \times U_{AB} \ = 12 \times 1,6.10^{ \ -19} \times 1,0.10^{ \ 5} \ = 1,92.10^{ \ -13} \ J$