Description d'un Mouvement

10 P 254 : Norme et vecteur.

1.a. $\overrightarrow{v_M} = \dfrac {\overrightarrow{dOM(t)}}{dt}$

1.b.$\overrightarrow{a_M} = \dfrac {\overrightarrow{v_M}}{dt} = \dfrac {d^2\overrightarrow{OM(t)}}{dt^2} $

2.a. Dans le cas d'un mouvement rectiligne, on a $a= \dfrac {dv}{dt}$. En effet, le vecteur vitesse n'ayant qu'une composante :$ \overrightarrow {v(t)} = v(t) \overrightarrow {u} $.

$$ \overrightarrow {a(t)} =\dfrac{d\overrightarrow {v(t)}}{dt} = \dfrac {dv(t)}{dt} \overrightarrow {u} $$

$$ \left \| \overrightarrow {a(t)} \right \| = a(t) = \left \| \dfrac {dv(t)}{dt} \overrightarrow {u} \right \| = \dfrac {dv(t)}{dt} $$

2.b. Dans le cas d'un mouvement circulaire, par exemple, le vecteur vitesse a au moins deux composante :

$$ \overrightarrow {v(t)} = v_x(t)\overrightarrow {i} +v_x(t)\overrightarrow {j}$$
$$ \overrightarrow {a(t)} = \dfrac {d\overrightarrow {v(t)}}{dt} = \dfrac {dv_x(t)}{dt}.\overrightarrow {i} + \dfrac {dv_y(t)}{dt}.\overrightarrow {j} $$
$$ \left \| \overrightarrow {a(t)} \right \| = a(t) = \left \| \dfrac {dv_x(t)}{dt}.\overrightarrow {i} + \dfrac {dv_y(t)}{dt}.\overrightarrow {j} \right \| = \sqrt {\left ( {\dfrac {dv_x(t)}{dt}} \right )^2 + \left ( {\dfrac {dv_y(t)}{dt}} \right )^2 } $$

11 P 254 : Saut d'un tremplin en vélo.

$$\left\{ \begin{array}{ll}
x(t)=3,39 \times t \\
y(t) = -4,9 \times t^2 + 5,87 \times t +2,0
\end{array}
\right.$$

1.a.

$ \overrightarrow{v_M(t)} = \dfrac {\overrightarrow{dOM(t)}}{dt} = \left\{ \begin{array}{ll}
        v_x(t)= \dfrac {dx(t)}{dt} = 3,39  \\
        v_y(t) = \dfrac {dy(t)}{dt} = - 4,9 \times t + 5,87
    \end{array}
\right.$

1b.

$ \overrightarrow{v_M} (0,1) = \left\{ \begin{array}{ll}
        v_x(0,1) = 3,39  \\
        v_y(0,1) = - 9,8 \times 0,1 + 5,87 = 4,89
    \end{array}
\right.$

$ v(0,1) = \left \| \overrightarrow{v_M}(0,1) \right\| = \sqrt {3,39^2 + 4,89 ^2 } = 5,95 \ m.s^{ \ -1}$

2.a.

$ \overrightarrow{a_M(t)} = \dfrac {\overrightarrow{dv(t)}}{dt} = \left\{ \begin{array}{ll}
a_x(t)= \dfrac {dx(t)}{dt} = 0  \\
a_y(t) = \dfrac {dy(t)}{dt} = -9,8
    \end{array}
\right.$

2b. Le vecteur accélération n'a qu'une composante verticale qui est constante.
2c. Quelque soit le temps, a(t) = 9,8. Il s'agit d'un mouvement uniformément accéléré.

12 P 254 : Lancer vertical.

$$\overrightarrow{OM}(t) = \left ( - \dfrac {1}{2} gt^2 + v_0 t +h \right ) \overrightarrow {k} $$

1.a.

$ \overrightarrow{v_M(t)} = \dfrac {\overrightarrow{dOM(t)}}{dt} = \left ( -gt +v_0 \right ) \overrightarrow {k}$

1b.

Le vecteur vitesse change de sens quand sa composante selon $\overrightarrow {k}$ change de signe. C'est-à-dire quand $-gt +v_0$ change de signe.

$ -gt + v_0 >0 $ pour $t< \dfrac {v_0}{g} $

$-gt+v_0<0$ pour $t>\dfrac{v_0}{g}$

$ \overrightarrow{a_M(t)} = \dfrac {\overrightarrow{dv(t)}}{dt} = \left ( -g \right ) \overrightarrow {k}$. Il s'agit du "vecteur accélération de la pesanteur"..

13 P 254 : Mouvement d'une valve de vélo.

1.a.

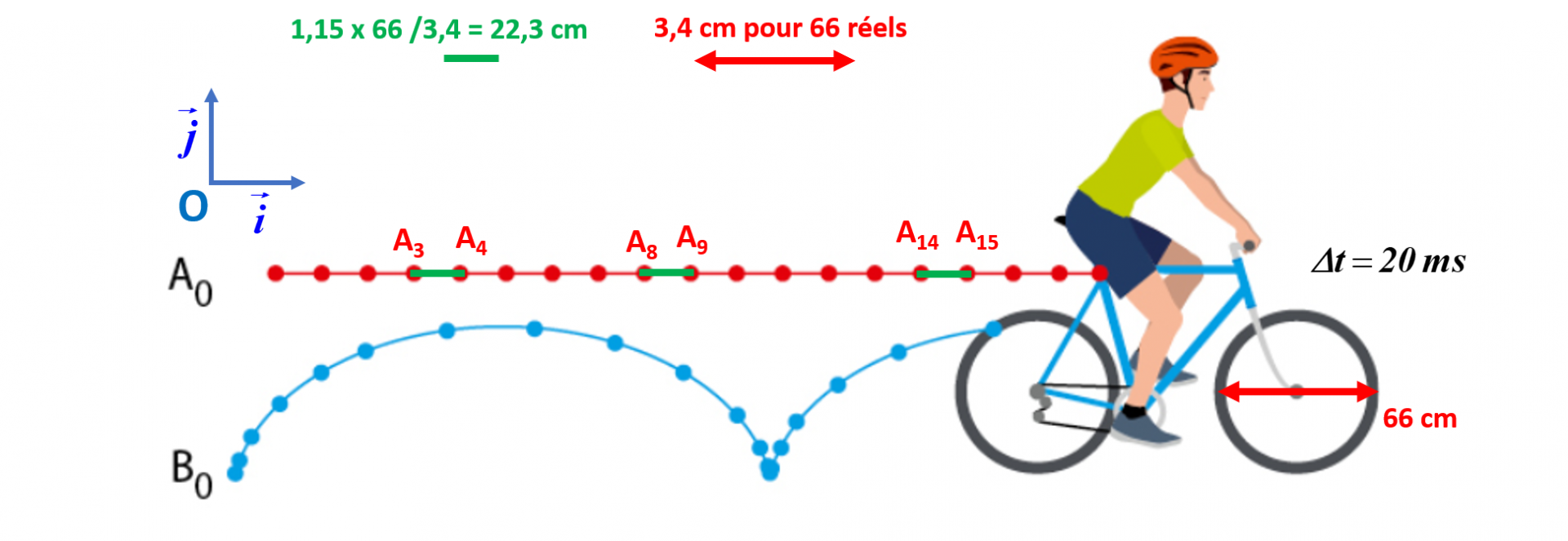13p254vitesse Pendant chaque intervalle de temps, la distance parcourue est la même :

$A_3A_4 = A_8A_9=A_{14}A_{15} =1,15 \times \dfrac{66}{3,4} = 22,3 cm$

La norme de la vitesse est : $ \left \| \overrightarrow {v_A }\right \| = \dfrac {22,3.10^{-2}}{20.10^{-3}} = 11,2 \ m.s^{-1} $

La vitesse est constante, le vecteur vitesse : $ \overrightarrow {v_A} = 11,2 \overrightarrow {i} $ aussi.

Nous sommes dans le cas d'un mouvement rectiligne uniforme.

1.b. Dans ce cas particulier d'un mouvement rectiligne uniforme, l'accélération est nulle : $\overrightarrow{a_A} = \overrightarrow {0}$ .

2.a,b.

Acc

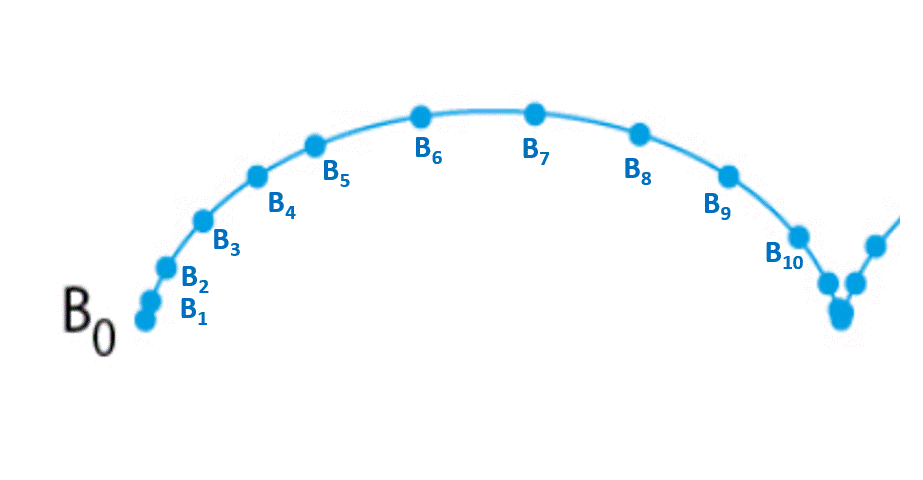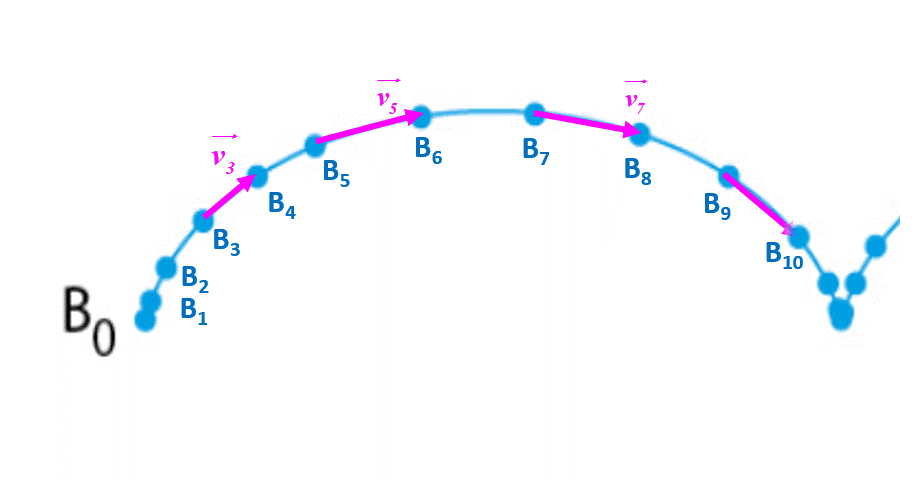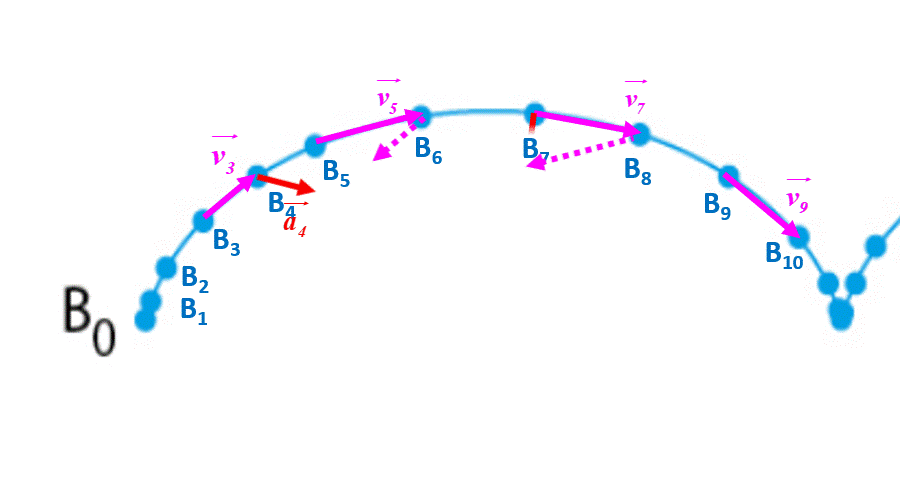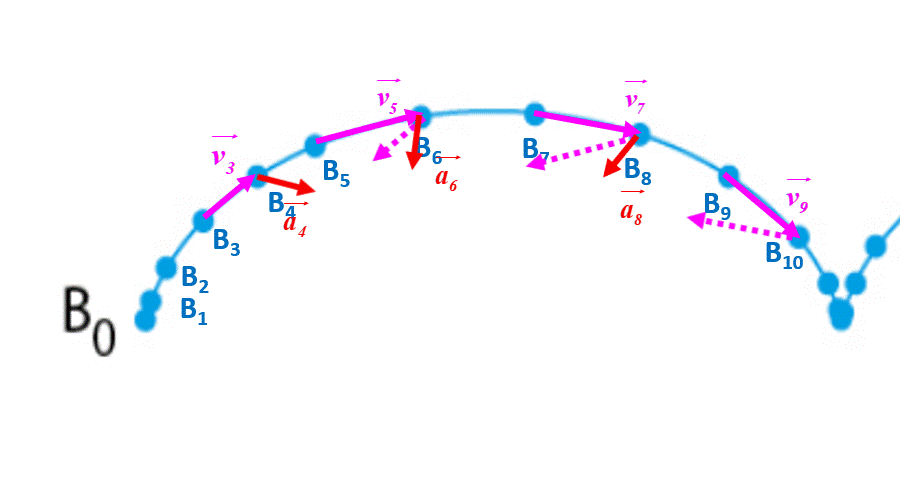
15 P 255 : Mouvements impossibles.

La base de Frenet :

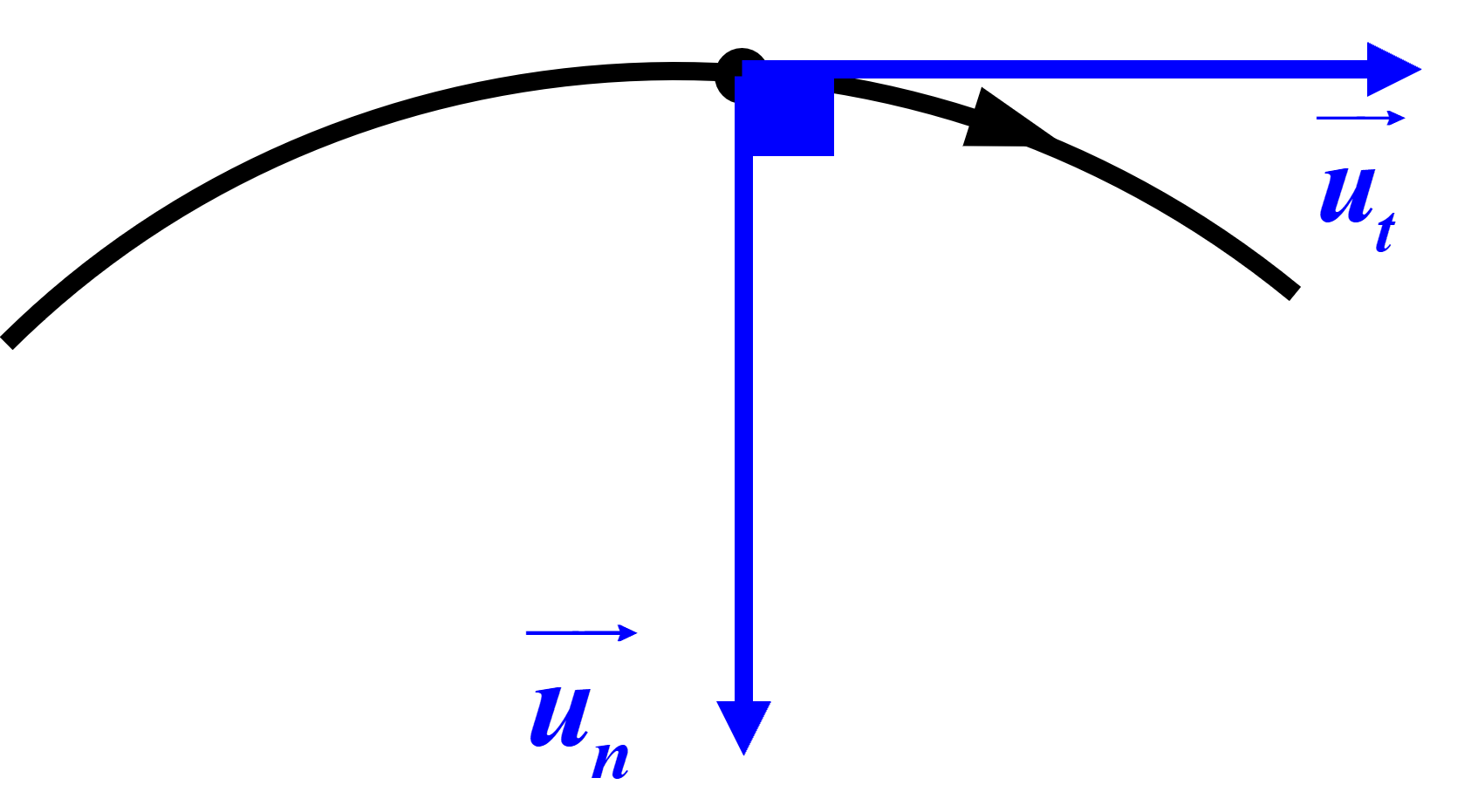Ci-contre, la représentation de la situation générale, avec la base de Frenet représentée au point considéré.

$ \overrightarrow{a}_{Frenet} = \left\{ \begin{array}{ll} a_t(t)= \dfrac {dv(t)}{dt} \\ a_n(t) = \dfrac {v^2}{R} \end{array} \right.$

Remarques :

$\bullet$ La composante selon $\overrightarrow {u_t}$ peut être positive (mouvement accéléré) ou négative (mouvement ralenti).

$\bullet$ La composante selon $\overrightarrow {u_n} \ , \ \dfrac{v^2}{R}$ est forcément positive. Le vecteur $\overrightarrow{a}$ est toujours centripète.

A		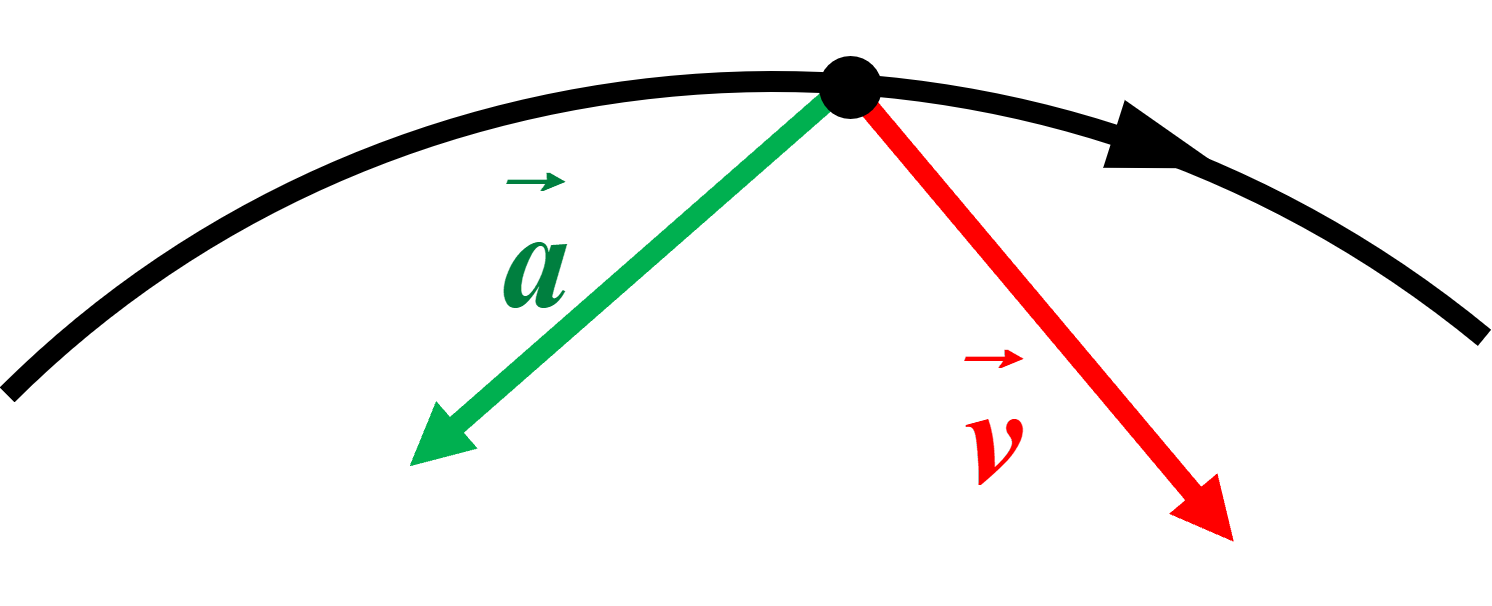Situation impossible : le vecteur vitesse doit être tangent à la trajectoire.
B		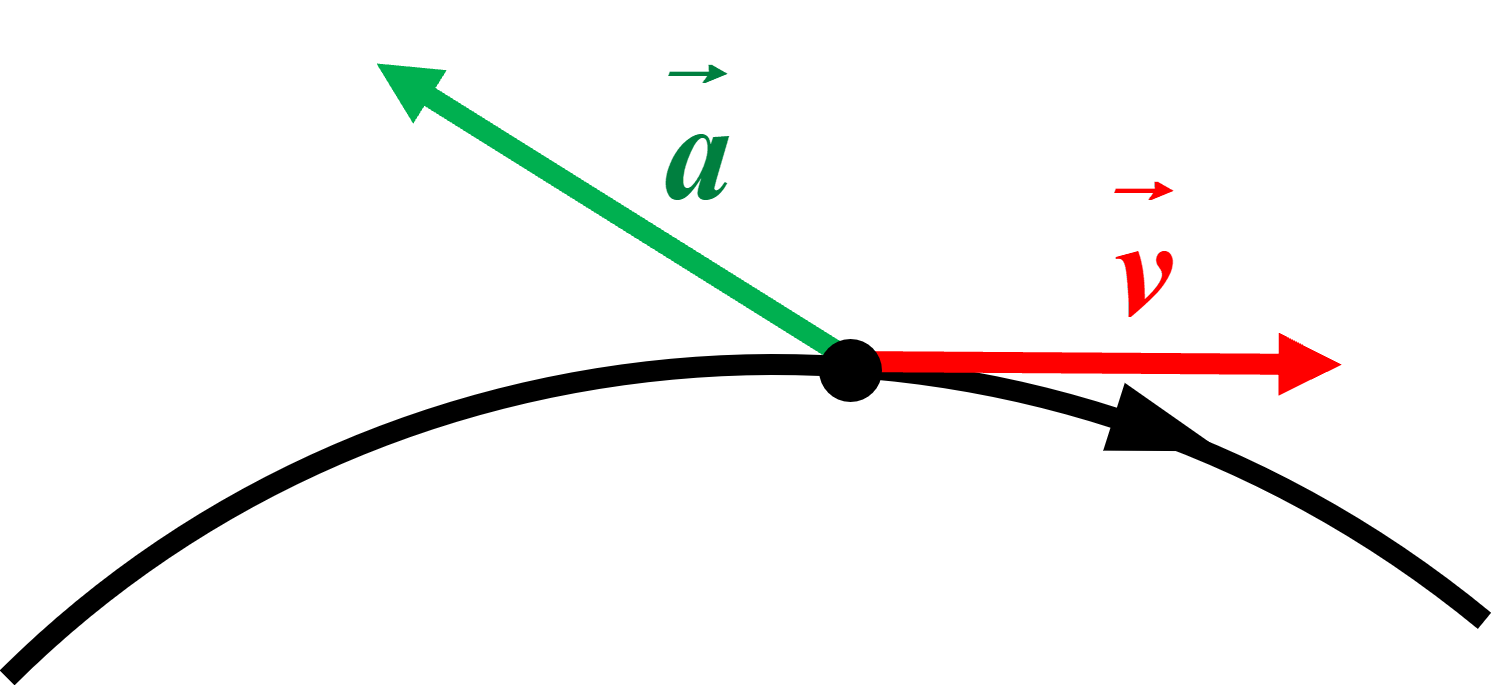Situation impossible : le vecteur accélération doit être centripète.
C		Situation possible : - le vecteur vitesse est tangent à la trajectoire. - dans le cas d'un mouvement rectiligne ralenti,le vecteur accélération est opposé au vecteur vitesse.
D		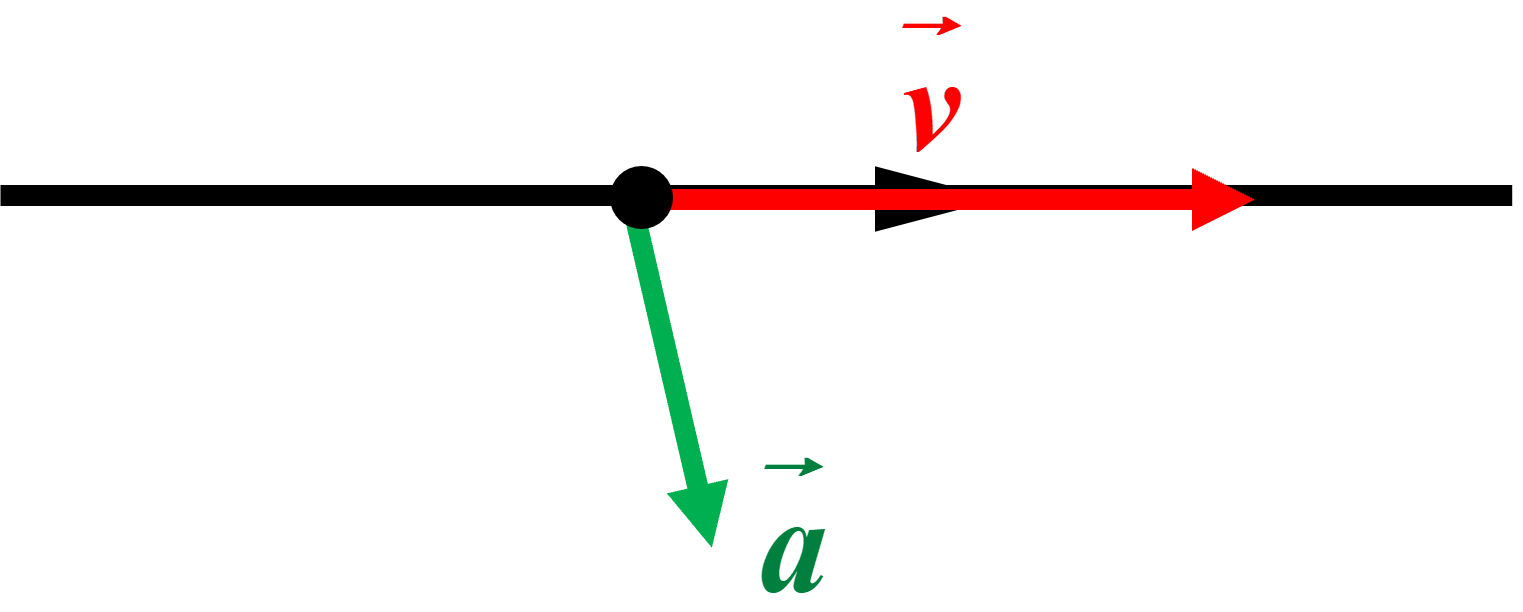Situation impossible : - le vecteur vitesse est tangent à la trajectoire. - dans le cas d'un mouvement rectiligne le vecteur accélération doit être colinéraire au vecteur vitesse.
E		Situation possible : - le vecteur vitesse est tangent à la trajectoire. - le vecteur accélération est centripète. - la composante de l'accélération selon $\overrightarrow {u_t} \ \left ( \dfrac{dv}{dt} \right )$ est positive (c'est le cas ici), dans le cas d'un mouvement accéléré, elle serait négative.
F		Situation impossible : - l'accélération doit être centripète.

17 P 255 : En virage.

1.
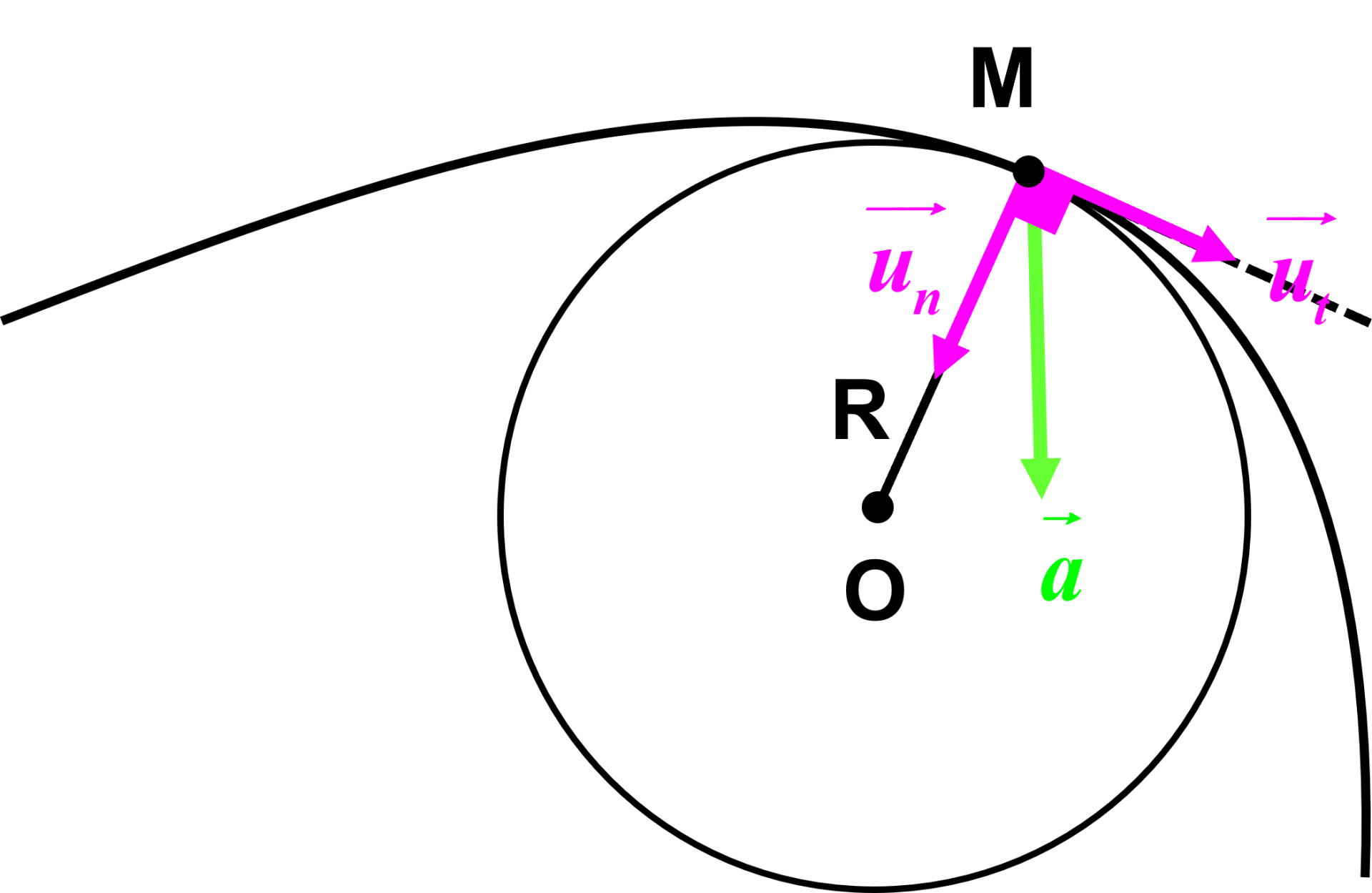2a.

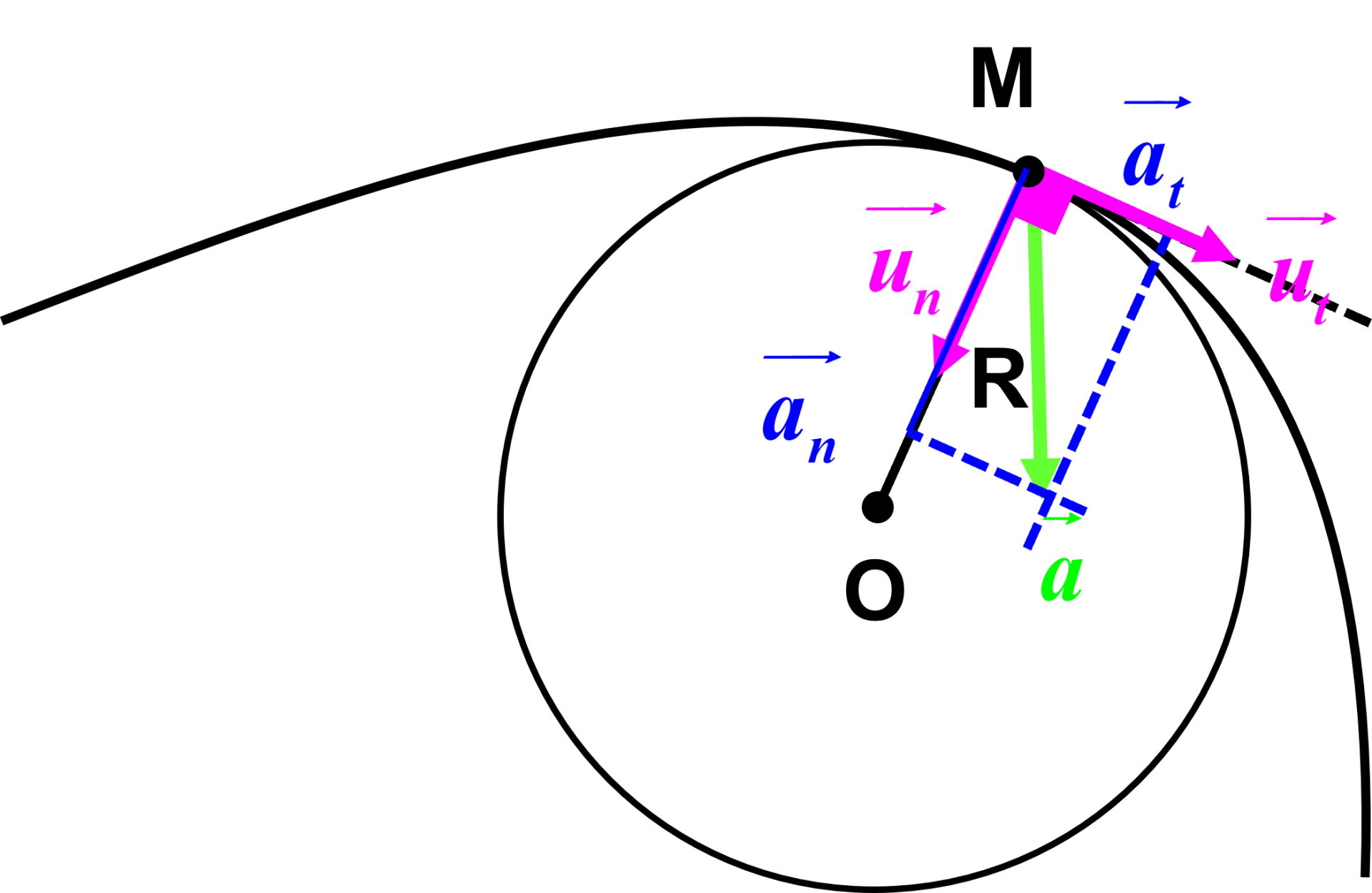2.b $\overrightarrow{a} = \dfrac {dv}{dt} \overrightarrow{u_t} + \dfrac {v^2}{R} \overrightarrow{u_n}$

Si la vitesse était constante, on aurait $ \dfrac {dv}{dt} = 0 $ et le vecteur accélération $ \overrightarrow{a} $ serait colinéaire au vecteur $\overrightarrow{u_n}$.

19 P 255 : Le looping.

1. $\overrightarrow{a} = \dfrac {dv}{dt} \overrightarrow{u_t} + \dfrac {v^2}{R} \overrightarrow{u_n}$

$ \overrightarrow{v} = \left\{ \begin{array}{ll}
        v_t(0,1) = 40,0  \\
        v_n =  0
    \end{array}
\right.$

$ \overrightarrow{a} = \left\{ \begin{array}{ll}
a_t = -6,5 \\
a_n = 106
\end{array}
\right.$

2a. $ \dfrac {dv}{dt} = -6,5 < 0 $ : la vitesse diminue selon $ \overrightarrow {u_t}$.

$ \dfrac {v^2}{R} = 106 > 0 $ : la vitesse augmente selon $ \overrightarrow {u_n}$.

2b. $ a_n = \dfrac {v^2}{R} = 106 \ m.s^{ \ -2} $ et $ v = 40 m.s ^{ \ -1}$. On a donc : $R = \dfrac {v^2}{a_n} = \dfrac {40^2}{106} = 15,1 \ m$

23 P 256 : Saut à ski.

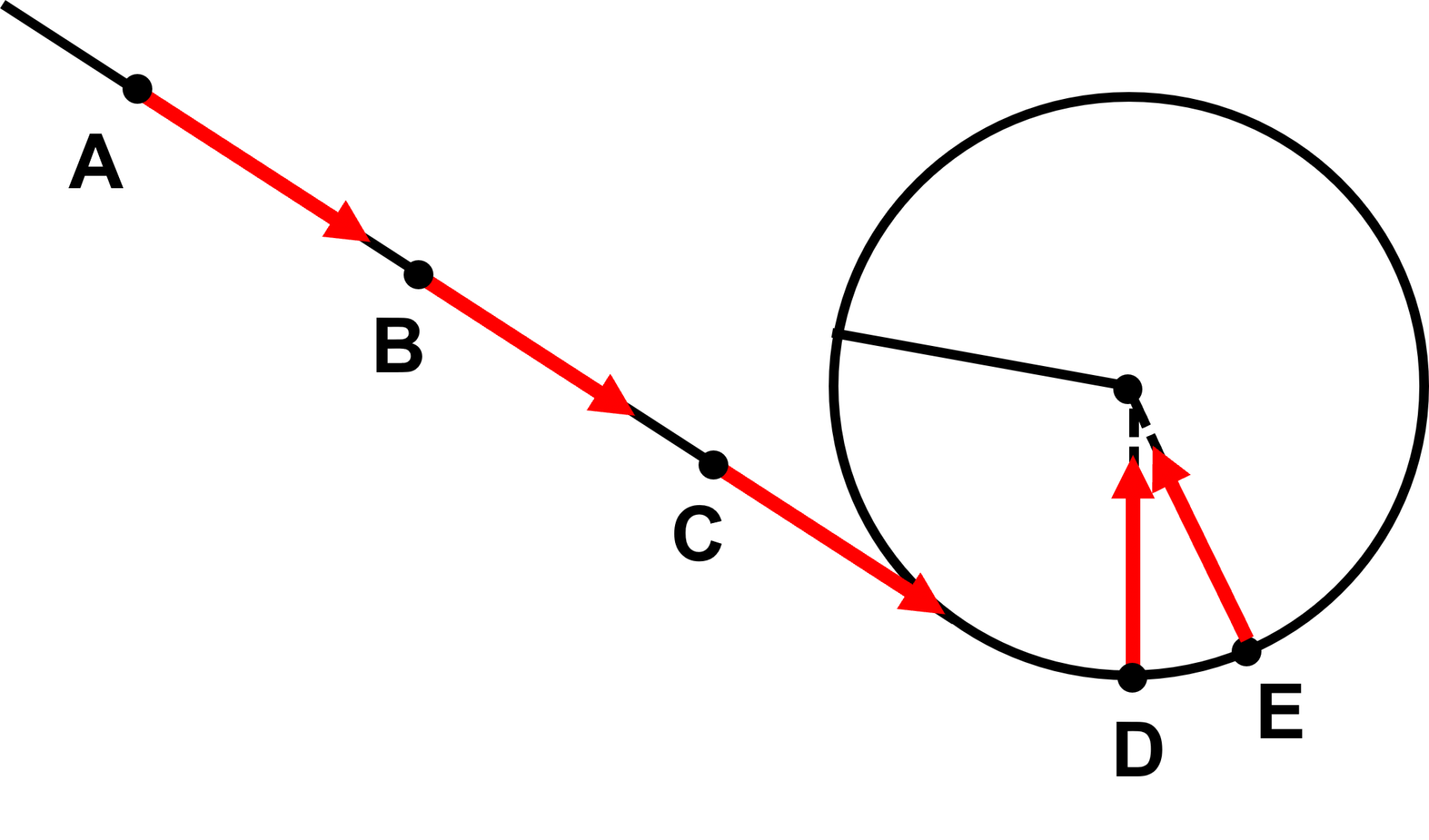Sur la portion rectiligne, la distance parcourue entre chaque point est la même.

Le mouvement est rectiligne uniforme.

Sur la portion circulaire, le mouvement est circulaire uniforme (la vistesse est constante), le vecteur vitesse est radial et centripète.

24 P 256 : Accélération à l'équateur.

1a. Ce point a un mouvementcirculaire uniforme.

1b. $P=2 \pi R = 2 \pi \times 6,4.10^3 = 40212 \ km = 4,02.10^{ \ 6 } \ m$.

$v = \dfrac {P}{T} = \dfrac {4,02.10^{ \ 6}}{24 \times 3600} = 465 \ m.s^{ \ -1} $.

1c. Dans ce cas, le vecteur accélération est orthogonal au vecteur vitesse et centripète et $ a = \dfrac {v^2}{R} = \dfrac {465^2}{6,4.10^6} = 3,4.10^{ \ -2} \ m.s^{ \ -2 } $

2. On ne retrouve pas la valeur de $9,8 \ m.s^{ \ -2 } $ : cette valeur correspond à l'accélération dans un référentiel terrestre, pas dans un référentiel géocentrique.

26 P 257 : Limite de résistance à l'accélération.

1. Dans la base de Frenet : $ \overrightarrow {a} = \dfrac {v^2}{R} \overrightarrow {u_n} $

2. $ v_{max} = \sqrt {a \times R}= \sqrt {9 \times g \times R} = \sqrt {9 \times9,81 \times 7,5 } = 25,7 \ m.s^{ \ - 1}$

3. La centrifugeuse parcourt $2 \times \pi \times R $ à la vitesse $v_{max}$. La période de rotation est donc : $T= \dfrac {2 \pi \ R}{v_{max}} = 1,8 \ s $

29 P 258 : La balançoire.

$ \overrightarrow {v} = \dfrac {L}{2} sin \left (2\pi \times t \right ) \overrightarrow {\tau } $

1. à $t=0 : v = \dfrac {L}{2} sin \left ( 2\pi \times 0 \right ) = 0 m.s^{-1}$

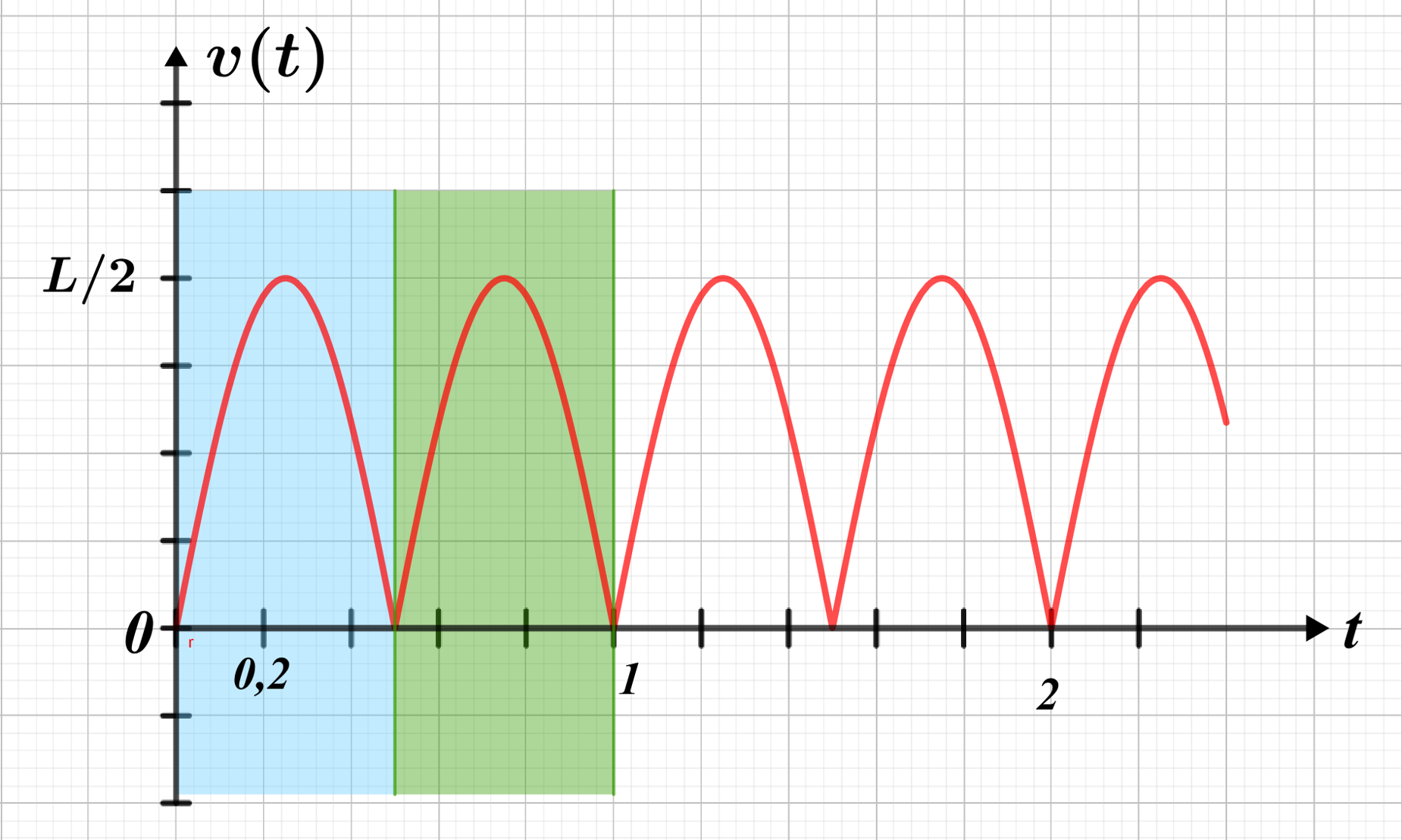
2. Exo 29

2a. Pour $0<t<0,25 \ s $ , v augmente, le mouvement est circulaire accéléré.

Pour $0,25<t<0,5 \ s $, v diminue, le mouvement est circulaire ralenti.

2b. Pour $0,5<t<0,75 \ s $ , v augmente le mouvement est circulaire accéléré.

Pour $0,75<t<1 \ s $, v diminue, le mouvement est circulaire ralenti.

2c. La période des oscillations est $T=1 \ s$

3a. Dans la base de Frenet, l'expression de l'accélération est : $\overrightarrow {a} = \dfrac {dv}{dt} \overrightarrow {\tau} + \dfrac {v^2}{R} \overrightarrow {n}$.

Ici : $\overrightarrow {a} = \pi \times L cos \left ( 2\pi t \right ) \overrightarrow {\tau} + \dfrac {L}{4} sin^2 \left ( 2 \pi t \right ) \overrightarrow {n}$.

3b. $a = \sqrt { \left (\pi \times L cos \left ( 2\pi t \right ) \right ) ^2 + \left ( \dfrac {L}{4} sin^2 \left ( 2 \pi t \right ) \right )^2}$.

La valeur de l'accélération varie en fonction du temps, elle n'est pas nulle. Le mouvement n'est pas uniforme.

31 P 259 : Le plan incliné en roller.

1. $ d\left ( t \right ) = 2,2t - \dfrac{1}{2} kt^2 $

donc : $ v \left ( t \right ) = 2,2 - kt$

donc : $a \left ( t \right ) = - k = - \ 4,9$

Le mouvement étant uniformément ralenti, la fonction $v(t) \ = 2,2 - kt$ doit être décroissante, la valeur de $k$ est donc positive.

Alors, $a(t) = -k$ et $a=|a(t)| = k = 4,9$

2a. La vitesse s'annule : $v \left ( t_0 \right ) = 0 \Leftrightarrow 2,2 - kt_0 = 0 \Leftrightarrow t_0 = \dfrac {-2,2}{k} = \dfrac {2,2}{4,9} = 0,45 \ s$

2b. La distance parcourue est alors : $d \left ( t_0 \right )= 2,2t_0 + \dfrac {1}{2} k t_0^2 \Leftrightarrow t_0 = 2,2 \dfrac {2,2}{4,9} - \dfrac {4,9}{2} \times \left ( \dfrac {2,2}{4,9} \right ) ^2 = \ 0,49 \ m$

Ambre se laisser "redescendre", elle était donc partie dans le sens de la montée, ayant parcouru la distance de $0,49 \ m \ < \ 0,60 \ m$, elle n'a pas atteint le haut de la rampe.

Lorsqu'elle atteint le bas du tremplin, sa position sera à nouveau nulle. Donc : $d(t) \ = 2,2t-2,45t^2 \ = t \left ( 2,2-2,45 \times t \right )$

Soit $t_{bas} = \dfrac{2,2}{2,45} \ = \ 0,90 \ s$. La durée de la descente sera : $t_{descente} \ = \ 0,90 - 0,45 \ = 0,45 \ s$

Sa vitesse sera : $v(0,90) \ = \ 2,2$ soit une valeur de la vitesse de $2,2 \ m.s^{ \ -1}$

33 P 260 : Du repère cartésien au repère de Frenet.

$\overrightarrow {v_M}(t) = \ - \ 4,8 \times \sin \left ( 5,0 \times t \right ) \overrightarrow {i} + 4,8 \times \cos \left ( 5,0 \times t \right ) \overrightarrow {j}$

1a. $ v_M(t) = \left \| \overrightarrow {v_M}(t) \right \| = \sqrt { \left ( - \ 4,8 \times \sin \left ( 5,0 \times t \right ) \right )^2 + \left ( 4,8 \times \cos \left ( 5,0 \times t \right ) \right )^2} $
$v_M(t) = \sqrt { \left ( - \ 4,8 \times \sin \left ( 5,0 \times t \right ) \right )^2 + \left ( 4,8 \times \cos \left ( 5,0 \times t \right ) \right )^2}$
$v_M(t) =\sqrt { 4,8^2 \times \sin^2 \left ( 5,0 \times t \right ) + 4,8^2 \times \cos^2 \left ( 5,0 \times t \right )}$
$v_M(t) =\sqrt { 4,8^2 \times \left ( \sin^2 \left ( 5,0 \times t \right ) + \cos^2 \left ( 5,0 \times t \right ) \right )}$
$v_M(t) =4,8 \times \sqrt { 1} = 4,8 \ m.s^{ \ -1} $

1b. La vitesse étant la même quelque soit le temps, le mouvement est uniforme.

2. $ \overrightarrow {a_M(t)} = \dfrac {d\overrightarrow {v_M(t)}}{dt} = - \ 4,8 \times 5 \times \cos \left ( 5,0 \times t \right ) \overrightarrow i + 4,8 \times 5 \times \sin \left ( 5,0 \times t \right ) \overrightarrow j$

$ \overrightarrow {a_M(t)} = - 24 \times \cos \left ( 5,0 \times t \right ) \overrightarrow i + 24 \times \sin \left ( 5,0 \times t \right ) \overrightarrow j$

$$ \left\{ \begin{array}{ll}
        \overrightarrow {\tau}= - \ \sin \left ( 5 t \right ) \overrightarrow {i} + \cos \left ( 5 t \right ) \overrightarrow {j}  \\
        \overrightarrow {n}= - \ \cos \left ( 5 t \right ) \overrightarrow {i} - \sin \left ( 5 t \right ) \overrightarrow {j}
    \end{array}
\right.$$

3a. $\overrightarrow {\tau} = \dfrac {1}{4,8} \overrightarrow {v}$. Donc : $\overrightarrow {v} = 4,8 \times \overrightarrow {\tau}$

3b. Donc :$\left \| \overrightarrow {v} \right \|= 4,8 \times \sqrt {\sin ^2 \left( 5t \right ) + \cos ^2 \left (5t \right )} = 4,8 \times \sqrt {1} = 4,8 \ m.s^{ \ -1}$

3c. $ \overrightarrow {a(t)} = \dfrac {dv}{dt} \overrightarrow {\tau} + \dfrac {v^2}{R} \overrightarrow {n} = 0 \times \overrightarrow {\tau} + \dfrac {4,8^2}{R} \overrightarrow {n} =\dfrac {4,8^2}{R} \overrightarrow {n} =\dfrac {23,04}{R} \overrightarrow {n} $

3d. D'après la question 2 :

$\left \|\overrightarrow {a_M(t)} \right \| = \left \|- 24 \times \cos \left ( 5,0 \times t \right ) \overrightarrow i + 24 \times \sin \left ( 5,0 \times t \right ) \overrightarrow j \right \|= 24 m.s^{ \ - \ 2}$

Donc : $ \dfrac {23,04}{R} =24 \ soit : R = \dfrac {23,04}{24} = 0,96 \ m $

35 P 261 : La tyrolienne.

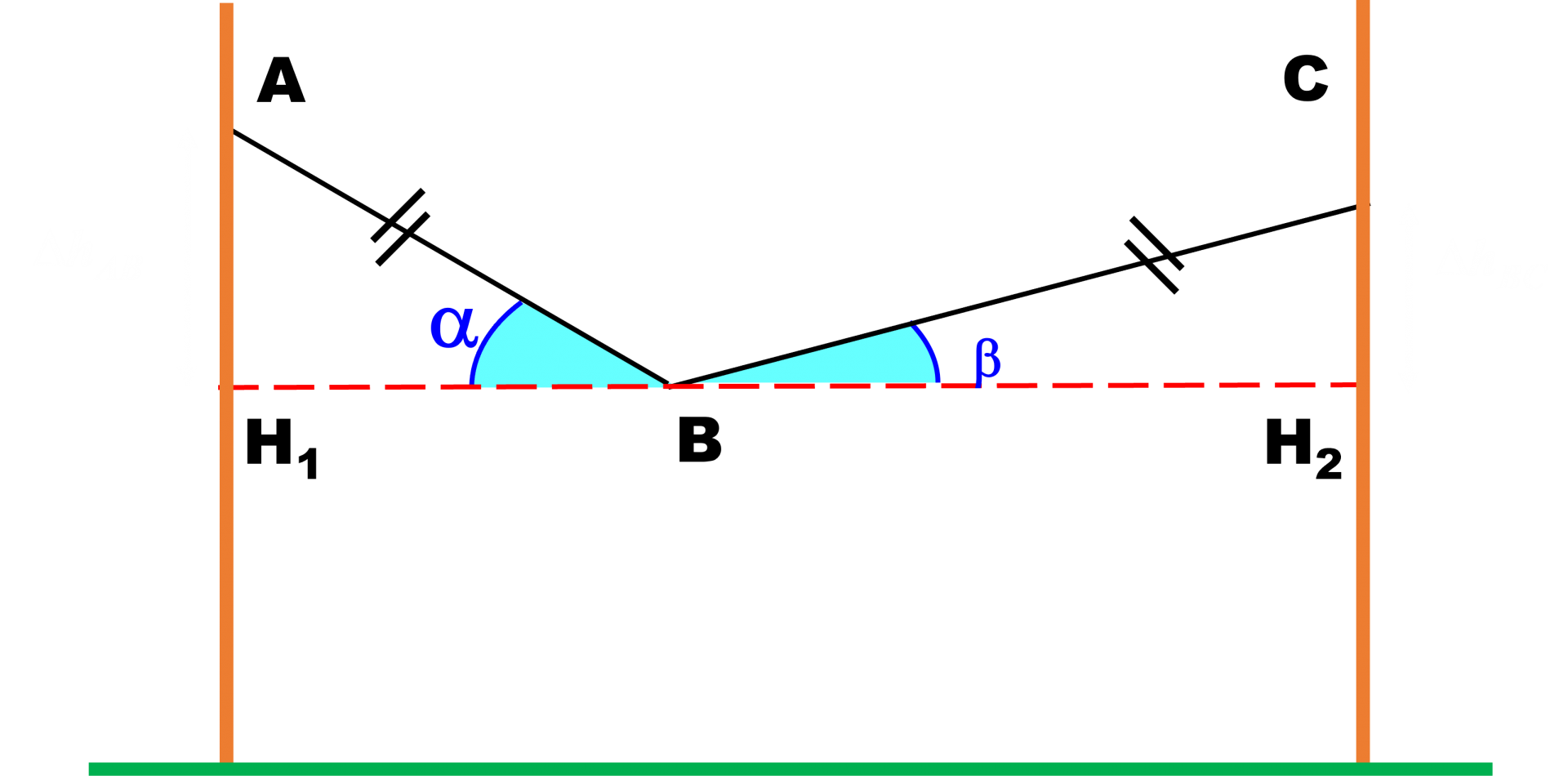
Exo35

1. De A à B, l'accélération a pour valeur : $ a = g \times \sin \alpha $. L'accélération est constante, selon la droite $ \left ( AB \right )$. Le mouvement est rectiligne uniformément accéléré.

De même, de B à C, l'accélération a pour valeur : $ a = g \times \sin \beta $. L'accélération est constante, selon la droite $ \left ( BC \right )$. Mais cette fois, l'accélératin est opposée au déplacemement : le mouvement est rectiligne uniformément ralenti.

2a. $ \overrightarrow {a_1} = g\sin \alpha \times \dfrac {\overrightarrow {AB}}{AB} $ et $ \overrightarrow {a_2} = \ - \ g\sin \beta \times \dfrac {\overrightarrow {BC}}{BC}$ .

Comme $ \alpha > \beta \ : \ \ a_1 \ > \ a_2$.

2b. En appliquant la conservation de l'énergie mécanique $ E_{C,A} \ + \ E_{P,A} \ = \ E_{C,C} \ + \ E_{P,C} $

Soit : $ \dfrac {1}{2} v_A^{ \ 2} + mgh_A = \dfrac {1}{2} v_C^{ \ 2} + mgh_C $ .

Soit : $ \dfrac {1}{2} v_C^{ \ 2} \ = mgh_C - mgh_A = mg \left ( h_C - h_A \right ) > \ 0$.

La vitesse en C n'est pas nulle.

Exercice n°43 P263 : le cyclotron.

On applique la formule donnée dans le document 2 : $R \ = \ \dfrac{m.v}{q.B} \ = \ \dfrac{1,64.10^{ \ -27} \times 9,8.10^{ \ -6}}{1,60.10^{ \ -19} \times 2,0} \ = 5,1.10^{ \ -2} \ m$.

Dans la formule donnée, $m \ , \ q$ et $B$ sont des constantes au cours du mouvement. Donc, si la vitesse augmente, le rayon de la trajectoire augment linéairement.

La longueur d'un demi-cercle est $d \ = \ \pi \times R$.

$\Delta t \ = \ \dfrac{d}{v} \ = \dfrac{\pi \times R}{v} \ = \ \dfrac{\pi \times m \times v}{v \times q \times B} \ = \ \dfrac{\pi \times m}{q \times B}$.

$v_x \ = \ \dfrac{dx}{dt} \ = \ \dfrac{qE}{m} \times t + v_0$ et $a_x \ = \ \dfrac{v_x}{dt} \ = \dfrac{qE}{m}$

On retrouve bien l'expression donée.

Problème.

Le mouvement se décompose en deux parties :

$\bullet rectiligne accéléré dans le champ électrique entre les deux D.

$\bullet circulaire uniforme dans le champ magnétique, dans les deux D.

Ainsi, la trajectoire a la forme d'une sprirale.

La vitesse n'augmente que lorsque la particule se trouve entre les D, sur une distance $L \times n$, où $n$ représente le nombre de passage entre les D (ici, $n=50$).

L'accélération est toujours la même car le champ électrique ne change pas de norme. Seul le sens du champ a changé. Tout se passe comme si la particule avait un mouvement rectiligne uniformément accéléré sur une distance de $50L$.

D'après la question 4., $v_x= \dfrac{qE}{m} \times t. $

Alors la durée nécessaire pour parcourir la distance $50L \ = \ \dfrac{1}{2} \times \dfrac{eQ}{m} \times t^2$.

Soit : $t \ = \ \sqrt{100 \times L \times \dfrac{m}{qE}}$.

Donc : $v_x \ = \ \dfrac{qE}{m} \times \sqrt{100 \times L \times \dfrac{m}{qE}} \ = \ 10 \times \sqrt{L \times \dfrac{qE}{m}}$

AN : $v_x \ = \ 10 \times \sqrt{1,0.10^{ \ -3} \times \dfrac{1,60.10^{ \ -19} \times 1,0.10^{ \ 7}}{1,67.10^{ \ -27}}} \ = \ 9,8.10^{ \ 6} \ m.s^{ \ -1}$

46 P 265 : S'insérer dans la circulation.

On se place dans le référentiel terrestre ayant pour origine la position de la voiture B à l'instant $t \ = \ 0$, instant de démarrage de la voiture A.

La voiture B est à la position $x \ = \ 0 \ m$. La voiture A est à la position $AB_{min}$

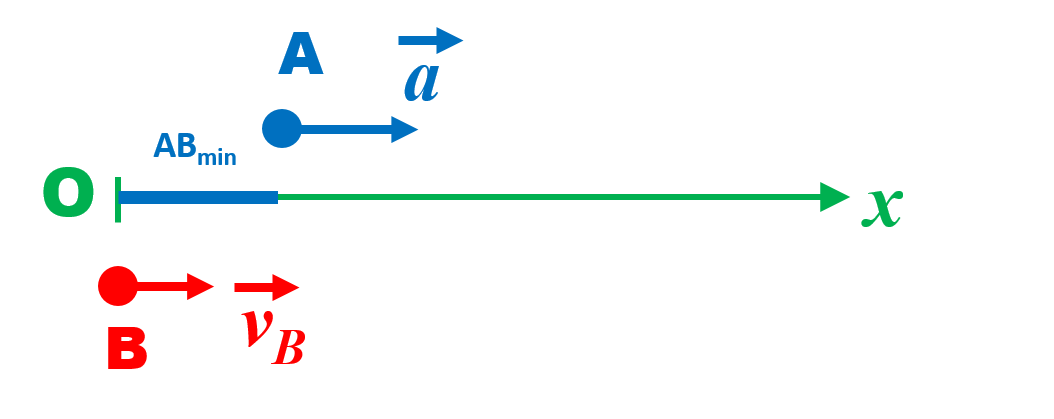
Exo46 1