Deuxième Loi De Newton
11 P 279 : Recherche du centre de masse.
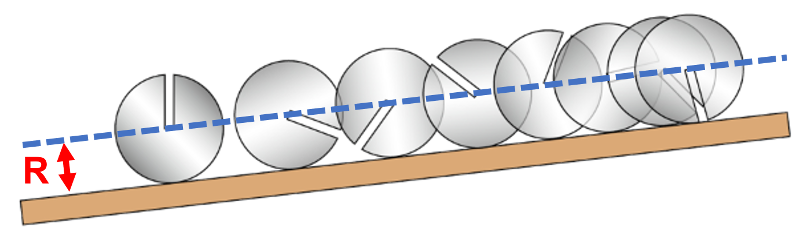
Le centre de masse du disque entaillé se trouve en son centre car il se déplace à la distance R du plan incliné.
14 P 279 : Référentiels galiléens courants.
• Le référentiel héliocentrique, utilisé pour étudier le mouvement des planètes du système pour un mouvement bref par rapport à leurs rotation autour du Soleil.
• Le référentiel géocentrique pour étudier le mouvement des satellites de la Terre, pour une durée suffisament brève par rapport à la rotation de la Terre sur elle-même.
• Le référentiel terrestre pour étudier le mouvement d'un corps dont le mouvement est relativement bref par rapport à la rotation de la Terre sur elle-même.
18 P 280 : Somme de forces.
1.
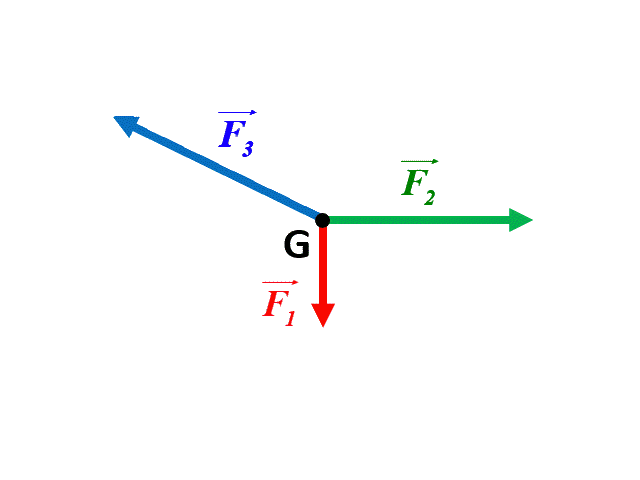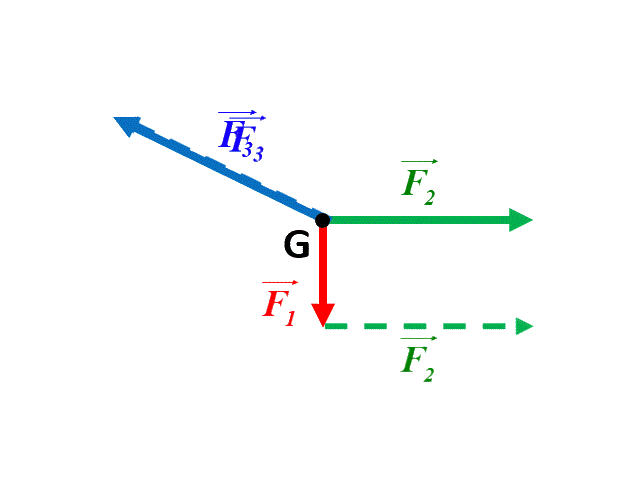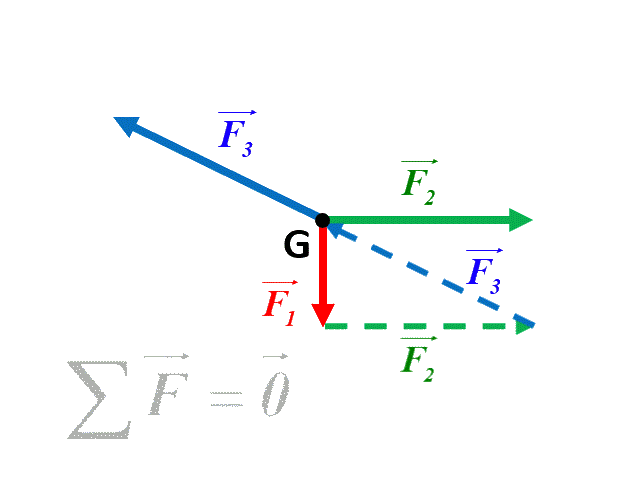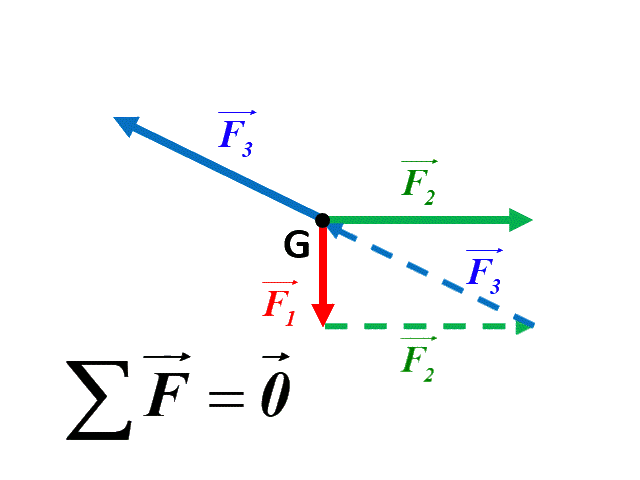
a |
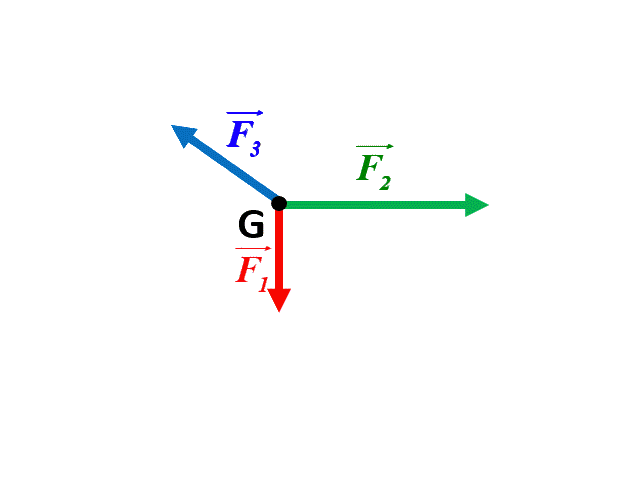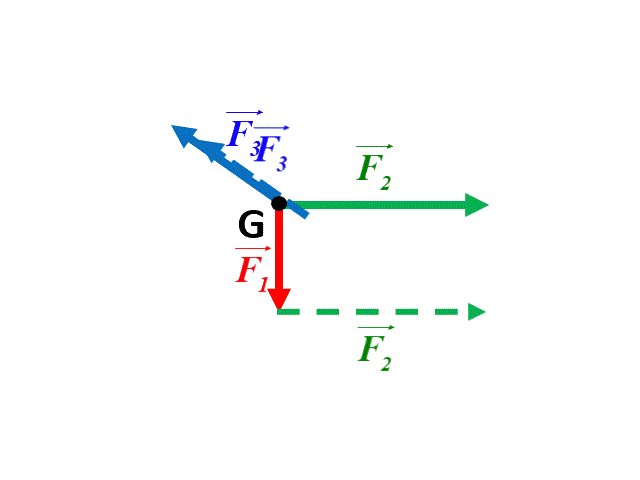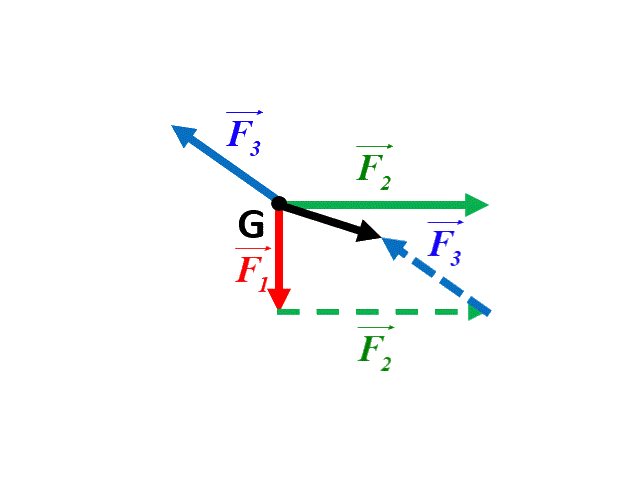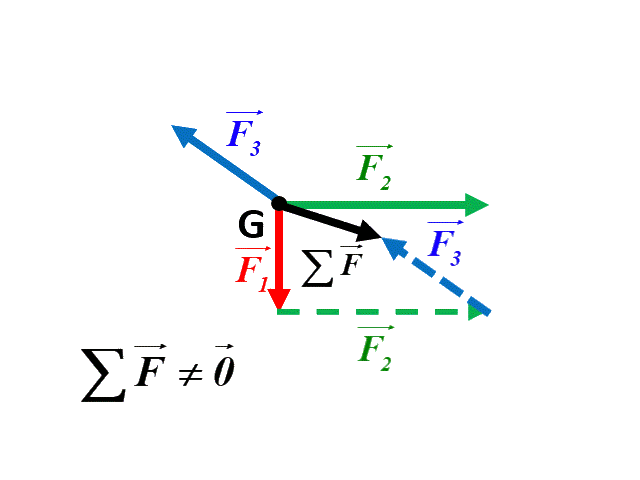
b |
2.
Dans le premier cas, la somme des forces étant nulle, le système est en équilibre. Par contre, dans le deuxième cas la somme des forces n'étant pas nulle, le système n'est pas en équilibre.
3.
Dans ce dernier cas, comme $ \Sigma \ \overrightarrow F \ = m \ \overrightarrow a $, l'accélération $\overrightarrow a$ a le même sens et la même direction que le vecteur $ \Sigma \ \overrightarrow F$.
20 P 280 : La piñata.
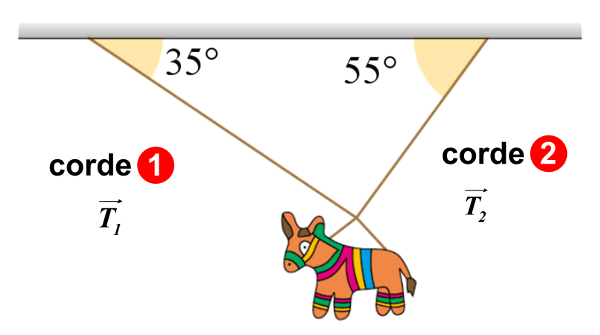
1. La piñata étant immobile, sa vitesse est nulle. Par conséquent, son accélération, dérivée de la vitesse est nulle aussi.
2. L' accélération, étany nulle aussi, la somme des forces s'y appliquant est nulle aussi.
3. La somme des forces s'y appliquant étant nulle, elle est à l'équilibre.
22 P 280 : Saut en parachute.
|
1. |
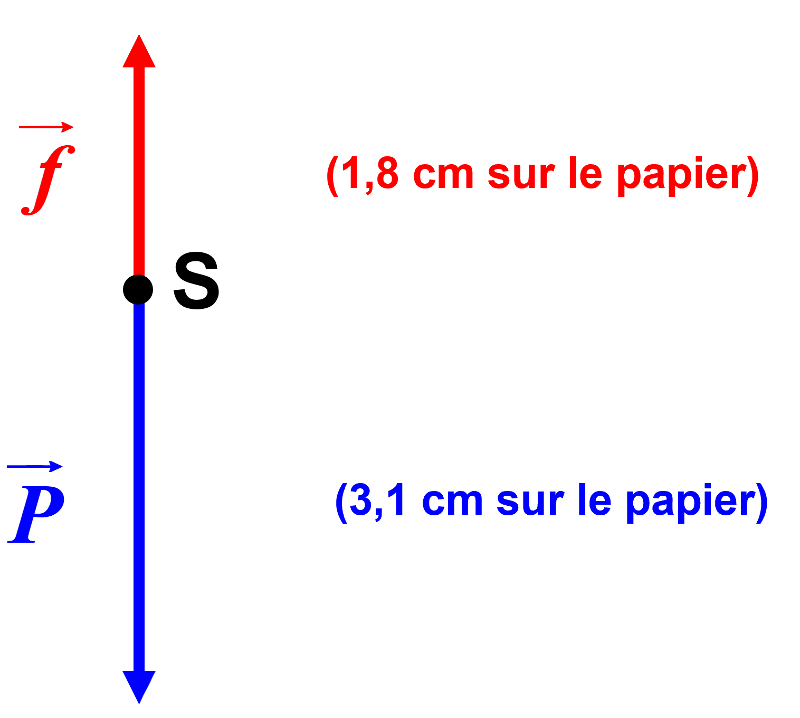 |
$\Sigma \overrightarrow F \ = \ \overrightarrow P \ + \ \overrightarrow f $. La valeur du poids est : $P \ = \ m \times g \ = 9,8 \times 90 \ = \ 882 N$. D'après l'échelle, la valeur des frottements est : $f \ = \ 512 N$ La valeur de la résultante : $F \ = \ 370 N$. Les deux forces étant verticales, la résultante est verticale, vers le bas ($P \ > \ f)$.
|
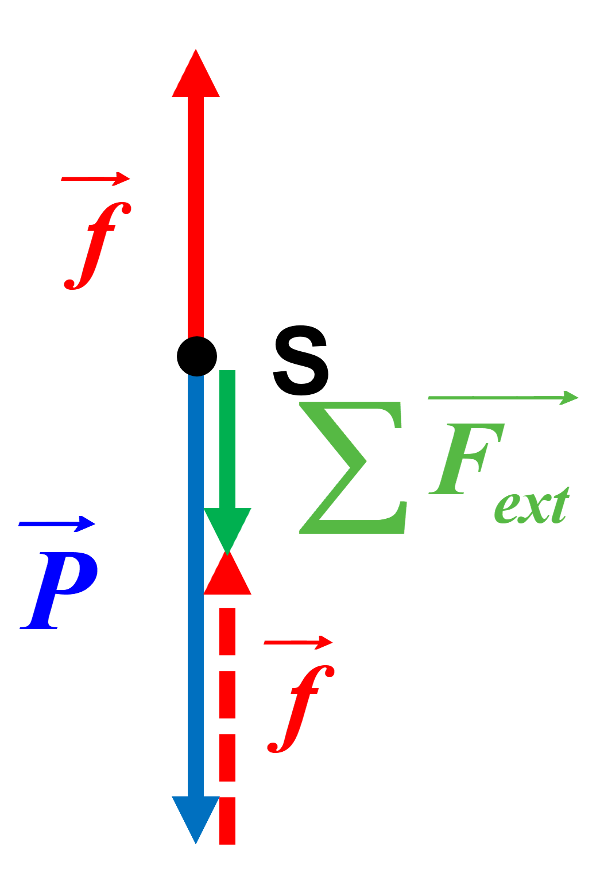
2. D'après la 2ème loi de Newton : $ \Sigma \overrightarrow F \ = \ m \times \overrightarrow a$.
Donc : $a \ = \ \dfrac {370}{90} \ = \ 4,1 \ m.s^{ \ -2}$.
29 P 282 : Ascension de la fusée Saturne V.
1. La phase de lancement sera étudiée dans le référentiel supposé galiléen.
2. Bilan des forces :
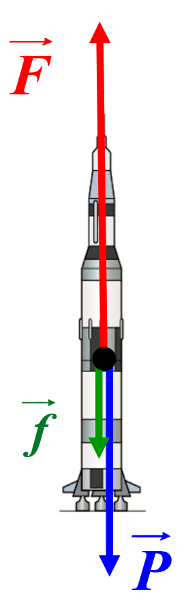 |
- Le poids $\overrightarrow P$: vertical, vers le bas. $P \ = \ m \times g \ = 2,3.10^{\ 6} \times 9,8 \ = \ 2,84.10^{ \ 7} \ N$ - La poussée des réacteurs $\overrightarrow F$, verticale, vers le haut. $F \ = \ 3,3.10^{ \ 7} \ N$ - Les frottements de l'air $\overrightarrow f$, verticale vers le bas. |
3.
D'après la deuxième loi de Newton : $\Sigma \overrightarrow F \ = m \times \overrightarrow a$.
On a donc : $\overrightarrow a \ = \ \dfrac {\overrightarrow F + \overrightarrow P}{m}$.
Soit : $a \ = \ \dfrac{3,3.10^{ \ 7} - 2,84.10^{ \ 7}}{2,9.10^{\ 6 }} = 1,58 \ m.s^{ \ -2}$.
Ajouter un commentaire
