Evolution temporelle Chimie

Exercice n°12 P99 : Suivi manométrique.

1. On utilise un manomètre pour mesurer l'augmentation de pression due au gaz $H_2$ produit.

2. Le seul paramètre qui varie dans le tableau est la concentration en ions $H_3O^{ \ +}$.

3. 

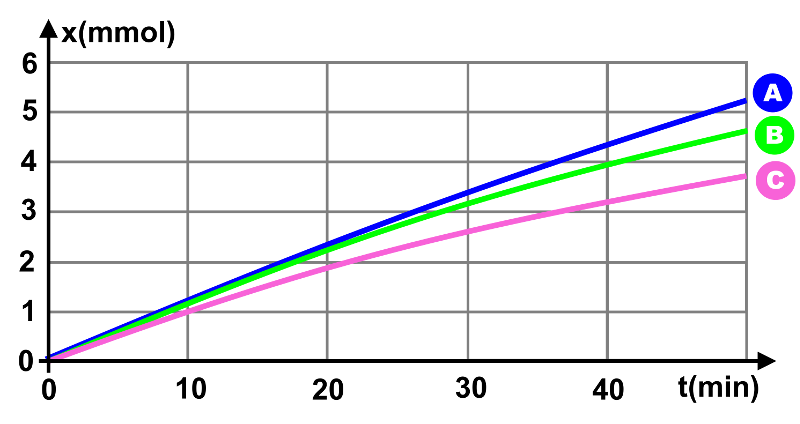
La vitesse de la réaction augmente avec la concentration... plus il y a de réactif dans le milieu, plus les réactifs ont de probabilté de se rencontrer.

La courbe A correspond à la concentration en $H_3O^{ \ + }$ la plus grande : $\left [ H_3O^{ \ + } \right ] \ = \ 0,50 \ mmol.L^{ \ -1}$.

Pour la courbe B : $\left [ H_3O^{ \ + } \right ] \ = \ 0,40 \ mmol.L^{ \ -1}$, et pour la courbe C : $\left [ H_3O^{ \ + } \right ] \ = \ 0,25 \ mmol.L^{ \ -1}$.

Exercice n°13 P99 : Eau de javel.

1. Ces espèces sont des catalyseurs car ils n'apparaissent pas dans la réaction chimique.

2. On parle de catalyse homogène lorsque le catalyseur est dans le même état physique que les réactifs. On aura une catalyse homogène avec lions ions $Co^{ \ 2+}$.

Si le catalyseur n'est pas dans le même état physique que les réactifs, on parle d e catalyse hétérogène. Ce sera le cas lors de l'utilisation des métaux.

3. Les métaux accélerant la dismutations des ions $ClO^{ \ -}$, il vaut mieux ne pas conserver l'eau de javel dans un contenant métallique .

Exercice n°16 P100 : Eau doxygénée et ions iodure.

1. 

$v_{I_2} (t_2) = \dfrac {4,06-0,00}{434-0} \ = \ 9,4.10^{ \ -3} \ mmol.L^{ \ -1}.s^{ \ -1}$

$v_{I_2} (t_4) = \dfrac {5,84-4,06}{930-434} \ = \ 3,6. 10^{ \ -3} \ mmol.L^{ \ -1}.s^{ \ -1}$.

2. $v(t_2) > v(t_4)$... la vitesse est plus grande au début de la réaction... les réactifs sont en plus grande quantité, la probabilité qu'ils se rencontrent et réagissent est plus grande.

Exercice n°17 P100 : Temps de demi-réaction.

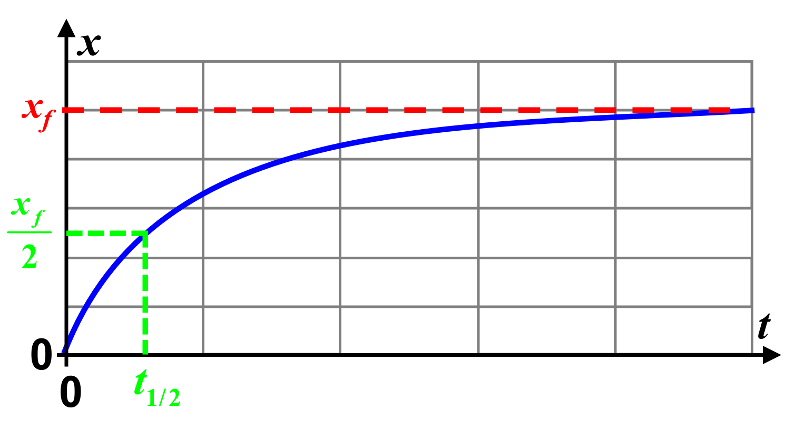
1. Le temps de demi-réaction est le temps nécessaire à la disparition de la moitié de la quantité finale du réactif limitant d'une réaction chimique.

2. 

3.

Exercice n°18 P100 : L'urée.

1.

Une réaction chimique est dite "d'ordre 1" lorsque la vitesse d'apparition ou de disparition $v$ d'une espèce chimique $A$ est proportionnelle à sa concentration : $v \ = \ k \ \times \ \left [ \ A \ \right ]$

2a.

$v_{OCN^{ \ - }} \ = \ \ = \ k_1 \ \times \ \left [ \ OCN^{ \ - } \ \right ]$

$v_{NH_4^{ \ + }} \ = \ \ = \ k_2 \ \times \ \left [ \ NH_4^{ \ + } \ \right ]$

$v_{OC(NH_2)_2} \ = \ \ = \ k_2 \ \times \ \left [ \ OC(NH_2)_2 \ \right ]$

2b.

	La représentation est fausse, car une vitesse volumique de disparition est positive.
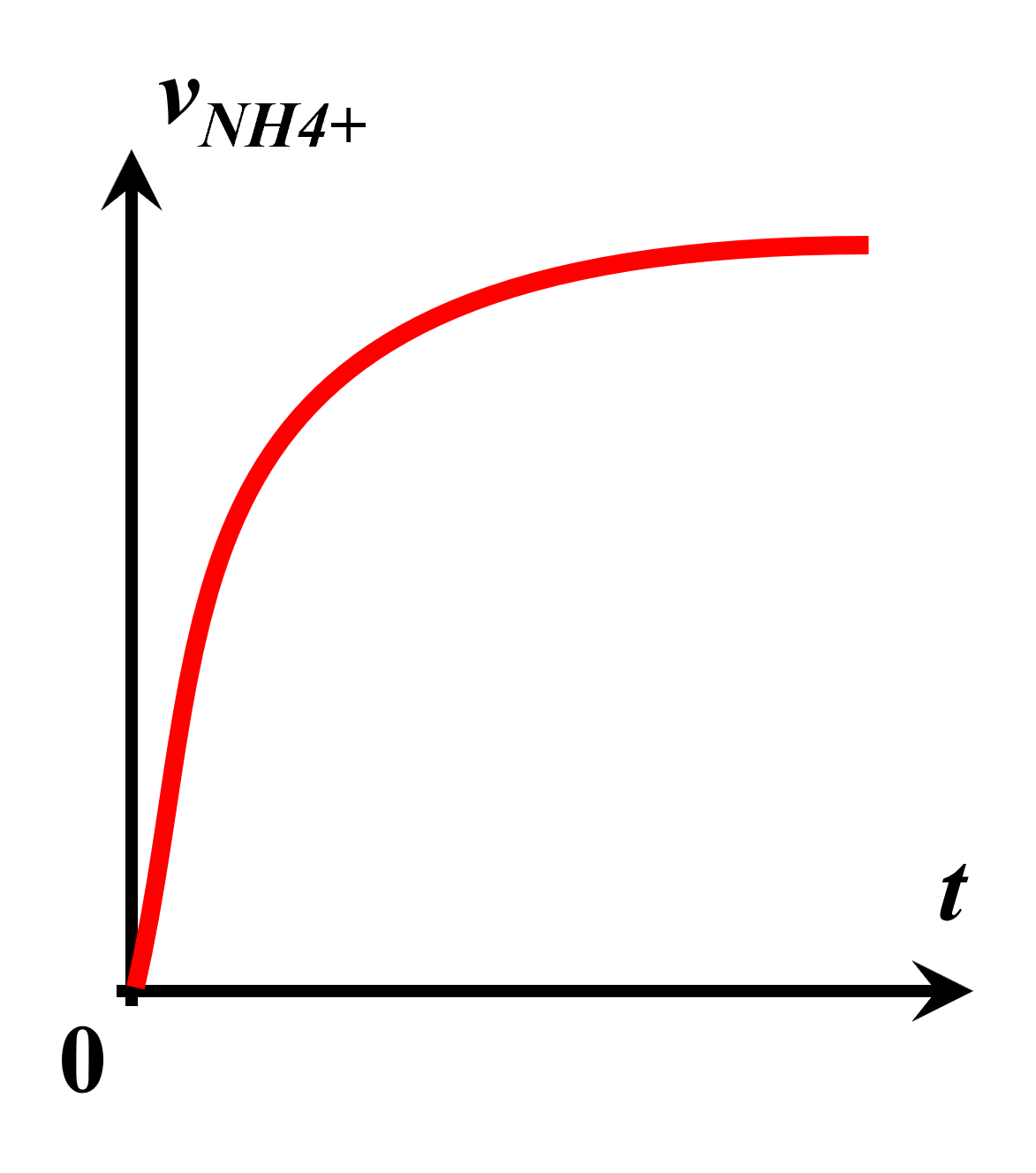
	La représentation est correcte, car la vitesse d'appartion d'un produit est proportionnelle à la concentration.
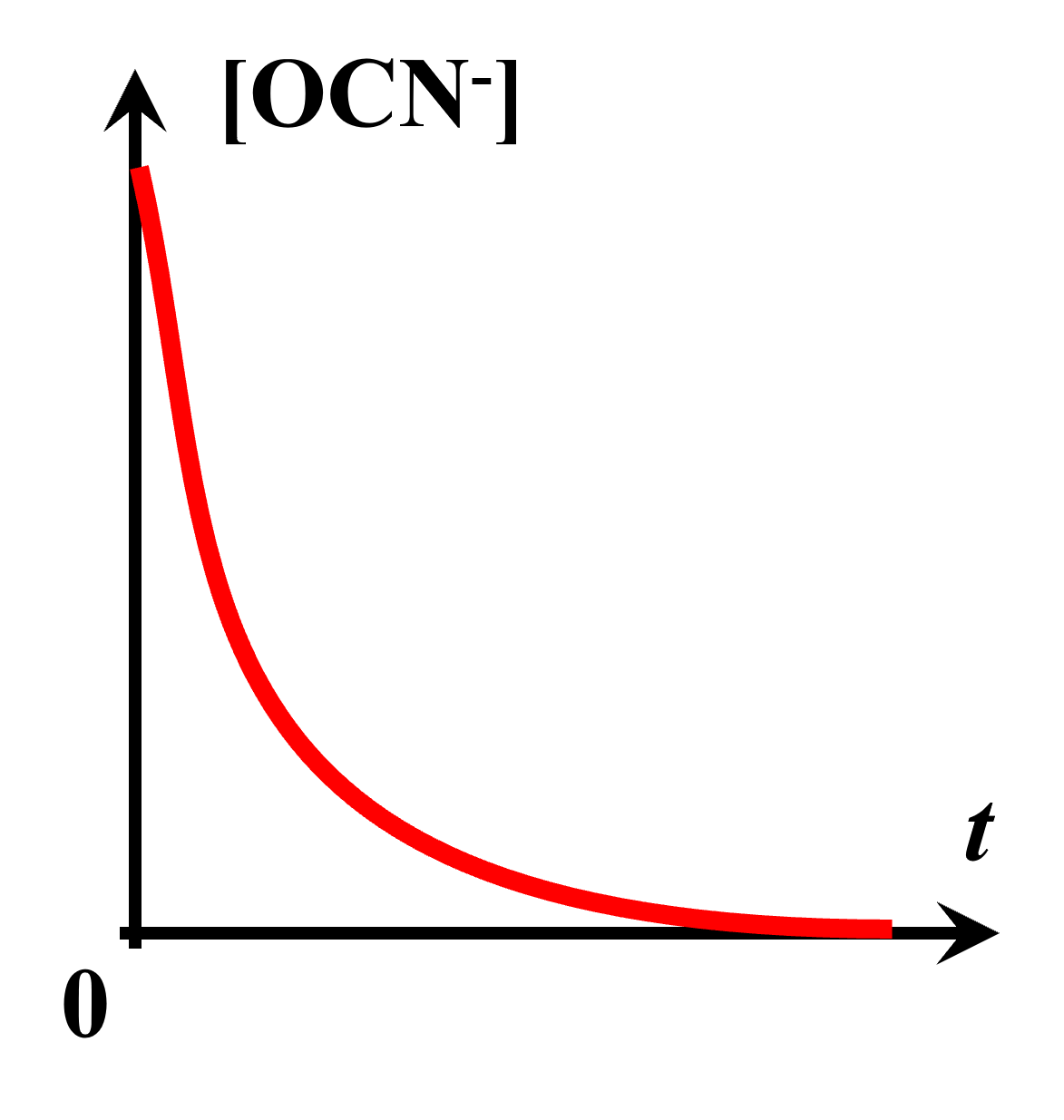
	La représentation est fausse : la vitesse d'apparition du produit diminue au cours du temps. En effet la quantité de réactif diminuant au cours du temps, la réaction sera de moins en moins rapide.
	La représentation est fausse : $OCN^{ \ - }$ étant un produit, sa concentration augmente au cours du temps.

2c.

$\bullet$ Le premier graphique pourrait représenter l'opposé de la vitesse de disparition de l'urée en fonction du temps.

$\bullet$ Le troisième graphique pourrait représenter la concentration en $NH_4^{ \ +}$ au cours du temps, l'espèce étant un produit, il y en a de plus en plus dans le milieu réactionnel. Cette concentration tendrait vers une valeur maximale.

$\bullet$ Le dernier graphique pourrait représenter la concentration en urée au cours du temps. Etant un réactif, il y enaurait de moins en moins, jusquà tendre vers 0 dans le cas d'une réaction totale.

Exercice n°24 P102 : Décomposition de l'éthanal.

$CH_3CHO_{(g)} \ \longrightarrow CH_{4(g)} \ + \ CO_{(g)}$

1. Les réactifs et les produits sont à l'état gazeux. D'après la loi des gaz parfaits : $PV \ = \ nRT$, le volume et la température étant constants, la quantité de matière de produit : $n \ = \ \dfrac{V}{RT} \times P$ est proportionnelle au volume. Le produit $\dfrac{V}{RT}$ est constant. En mesurant la pression $P$, on connaitra la quantité de matière en éthanal $CH_3CHO$.

2.Le temps de demi-réaction est le temps nécessaire à la disparition de la moitié de la quantité finale du réactif limitant d'une réaction chimique. Graphiquement, on détermine $t_{1/2} \ = \ 60 \ min$

3. A 400°C, la réaction sera plus lente.

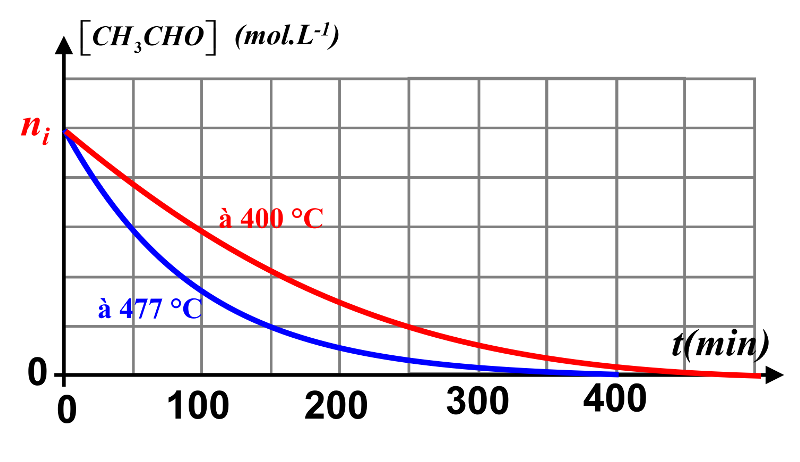
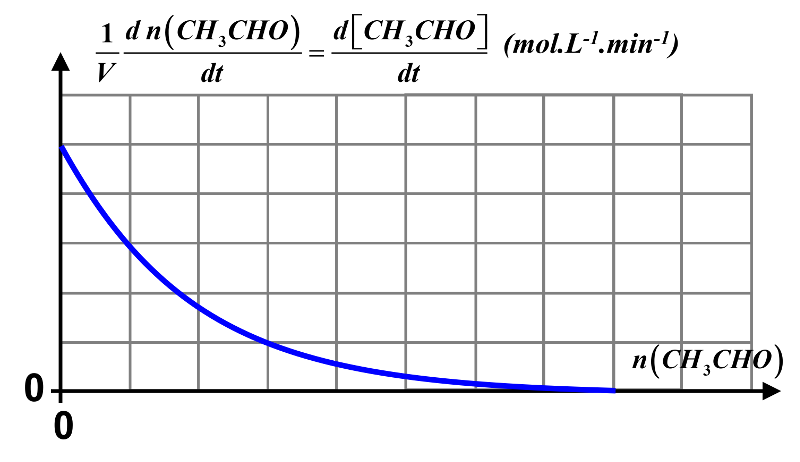
4. La quantité de réactif diminuant, vitesse de réaction diminue en fonction de cette quantité.

Exercice n°28 P102 : Roches calcaires.

1a.

$ \begin{array} { c | c | c | c | c | c | c | c} Réaction & \ \ CaCO_{3(aq)} \ & + \ 2 \ H_3O_{(aq)}^{ \ +} & \longrightarrow & \ \ Ca^{ \ 2+}{(aq)} \ & \ + \ CO_{2(g)} & \ + \ 3 \ H_2O_{(l)}\\ \hline t_{initial} & n_1 & n_0\left( H_3O^{ \ + } \right ) & & 0 & 0 & solvant \\ t & n_1 \ - \ x & n_0\left( H_3O^{ \ + } \right ) - \ -2x & & x & \ x & solvant \\ t_{final} & n_{1,f} \ - x_f & n_0\left( H_3O^{ \ + } \right ) \ - \ 2x_f & & x_f & x_f & solvant \\ \end{array} $

$\fbox{$n \left (H_3O^{ \ + } \right ) \ = \ n_0\left( H_3O^{ \ + } \right ) \ - \ 2x$ }$

1b. $v \ = \ \dfrac{n_0\left( H_3O^{ \ + } \right ) \ - \ 2x}{dt} \ = \dfrac{1}{2} \times \dfrac{dx}{dt}$

2a.

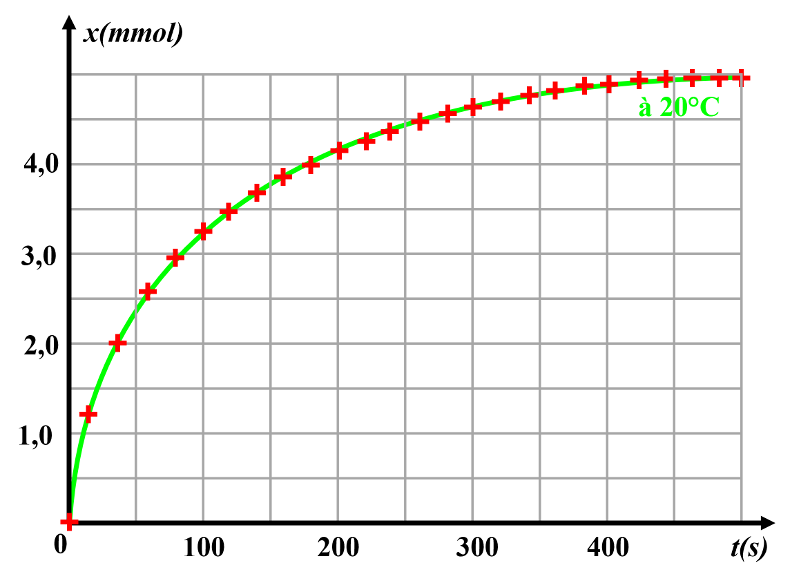
Au cours du temps, la pente de la courbe diminue : la vitesse diminue.

2b.

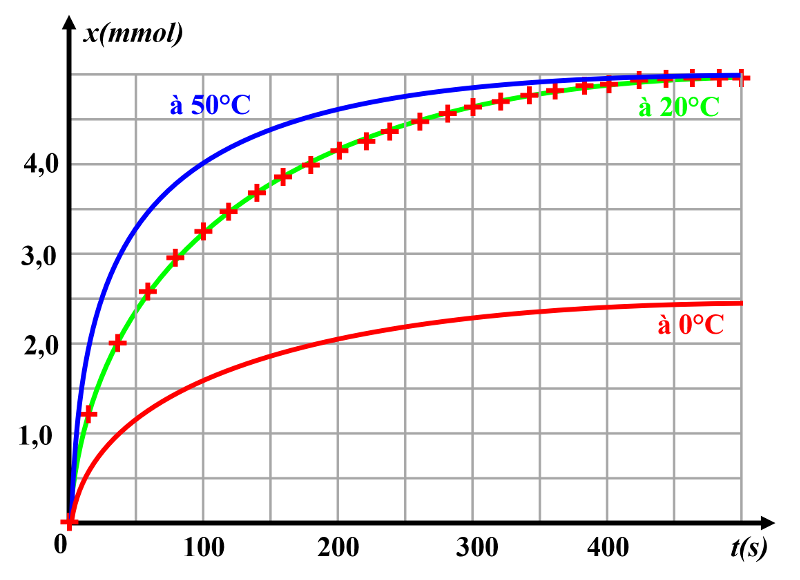
2b. La température diminuant, l'agitation microscopique diminue aussi, ce qui diminue la probabilité que les molécules se rencontrent pour réagir.

3a. Le temps de demi-réaction est le temps qu'il faut pour que l'avancement final de la réaction soit atteint.

3b.

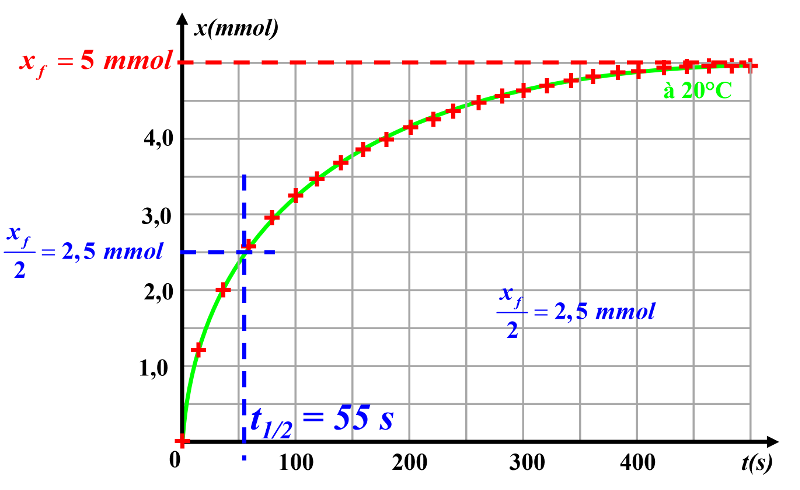
Le temps de demi-réaction est environ de 55 s

Exercice n°29 P105 : Eau oxygénée et ions tartatre.

1. L'acide sulfurique concentré acidifie le milieu et que la réaction ait lieu.

2a.

$$ \begin{array} { c c c c c c c c c} \ 5 \ H_2O_{2(aq)} \ & + \ 10 \ H_3O_{(aq)}^{ \ +} & \ + \ 10 \ Co^{ \ 2+}_{(aq)}& \longrightarrow & \ \ 10 \ Co^{ \ 3+}_{(aq)} \ & \ + \ 20 \ H_2O_{(l)} & & \ (1)\\ C_4H_4O_{(aq)}^{ \ 2-} & \ + \ 10 \ Co^{ \ 3+}_{(aq)} & \ + \ 10 \ H_2O_{(aq)} & \longrightarrow & \ 8 \ H_3O{(aq)}^{ \ +} & \ + \ 4 \ CO_{2(g)} & + \ 10 \ Co^{ \ 2+}_{(aq)} \ & (2) \\ \hline \\ \ 5 \ H_2O_{2(aq)} & \ + \ C_4H_4O_{(aq)}^{ \ 2-} & + \ 2 \ H_3O_{(aq)}^{ \ +} & \longrightarrow & \ + \ 4 \ CO_{2(g)} & \ + \ 10 \ H_2O_{(l)} \\ \end{array} $$

2b. Les ions $Co^{ \ 2+}$ n'apparaissent plus dans la réction-bilan. Il s'agit d'un catalyseur.

2c.

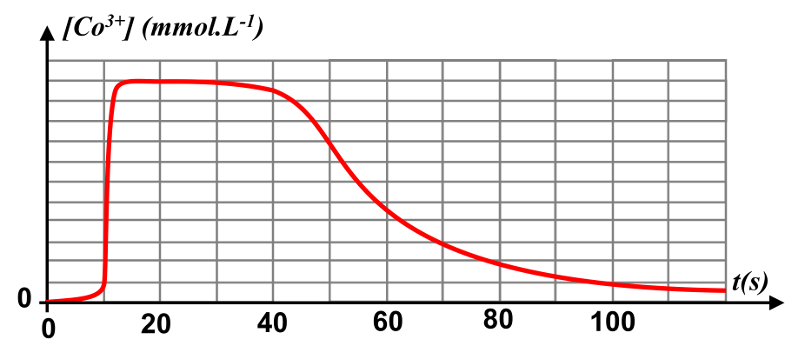
Les ions $Co^{ \ +3}$ apparaissent rapidement au début de la réaction, puis disparaissent totalement. Ils sont bien formés au début. Leur disparition montre qu'ils sont totalement "reformés". Les ions $Co^{ \ 2+}$ ont bien été transformés pour réapparaître intégralement, c'est leur rôle de catalyseur.

2d,e.

Audébut de la réaction, les ions $Co^{ \ 2+}$ imposent leur couleur verdâtre au milieu. L'apparition des ions $Co^{ \ 3+}$ appraissant, ils vont imposer leur couleur rosée aux dépens de la couleur verdâtre. La solution est verdâtre au début de la réaction, puis réapparaît à partir de $t \ = \ 80 \ s$.

2f. La couleur du milieu se modifiant, on pourra suivre l'évolution de la réaction en utilisant ce paramètre. IL faudra régler le spectrophotommètre au maximum d'absorbance des ions $Co^{ \ 3+}$.