Force des acides et des bases

Exercice n°9 P 173 : Produit ionique de l'eau.

1. $K_e \ = \ \left [ H_3O^{ \ +}_{(aq)} \right ] \times \left [ HO^{ \ -}_{(aq)} \right ] \ = \ 10^{ \ -14}$

2. $2 \ H_2O_{(l)} \ \overrightarrow{\longleftarrow} \ H_3O^{ \ +}_{(aq)} \ + \ HO^{ \ -}_{(aq)} $

Exercice n°11 P 173 : Quelques boissons.

Jus de pomme : $pH \ = \ 3,2.$

Donc : $ \left [ H_3O^{ \ +}_{(aq)} \right ] \ = \ 10^{ \ -pH} \ = \ 10^{ \ -3,2} \ = \ 6,31.10^{ \ -4} \ mol.L^{ \ -1}$

Alors : $\left [ HO^{ \ -}_{(aq)} \right ] \ = \ \dfrac{K_e}{\left [ H_3O^{ \ +}_{(aq)} \right ]} \ = \ dfrac{10^{ \ -14}}{10^{ \ -3,2}} \ =  \ 10^{ \ -10,8} \ = \ 1,58.10^{ \ -11} \ mol.L^{ \ -1}$.

Lait : $\left [ H_3O^{ \ +}_{(aq)} \right ] \ = \ 2,0.10^{ \ -7} \ mol.L^{ \ -1}$

Donc : $ pH \ = \ -log \left ( \left [ H_3O^{ \ +}_{(aq)} \right ] \right )  = \ -log \left ( 2,0.10^{ \ -^7} \right ) \ = \ 6,70.$

Alors : $\left [ HO^{ \ -}_{(aq)} \right ] \ = \ \dfrac{K_e}{\left [ H_3O^{ \ +}_{(aq)} \right ]} \ = \ dfrac{10^{ \ -14}}{2,0.10^{ \ -7}} \ = \ 5,0.10^{ \ -8} \ mol.L^{ \ -1}$.

Eau minérale : $\left  [ HO^{ \ -}_{(aq)} \right ] \ = \ 3,1.10^{ \ -7} \ mol.L^{ \ -1}$

Donc : $ \left [ H_3O^{ \ +}_{(aq)} \right ] \  = \ \dfrac{K_e}{\left [ HO^{ \ -}_{(aq)} \right ]} \ = \ \dfrac{10^{ \ -14}}{3,1.10^{ \ -7}} \ = \ 3,23.10^{ \ -8} \ mol.L^{ \ -1}$.

Alors : $pH \ = \ -log \left ( \left [ H_3O^{ \ +}_{(aq)} \right ] \right )  \ = \ -log \left ( 3,23.10^{ \ -8} \right ) \ = \ 7,49$.

Soda au cola : $pH \ = \ 2,5.$

Donc : $ \left [ H_3O^{ \ +}_{(aq)} \right ] \ = \ 10^{ \ -pH} \ = \ 10^{ \ -2,5} \ = \ 3,16.10^{ \ -3} \ mol.L^{ \ -1}$

Alors : $\left [ HO^{ \ -}_{(aq)} \right ] \ = \ \dfrac{K_e}{\left [ H_3O^{ \ +}_{(aq)} \right ]} \ = \ dfrac{10^{ \ -14}}{10^{ \ -2,5}} \ =  \ 10^{ \ -11,5} \ = \ 3,16.10^{ \ -12} \ mol.L^{ \ -1}$.

Exercice n°12 P 173 : L'acide perchlorique.

$HClO_{4,(aq)} \ + \ H_2O_{(l)} \ \longrightarrow \ ClO_{4,(aq)}^{ \ -} \ + \ H_3O^{ \ +}_{(aq)}$

1. Le couple correspondant est : $HClO_{4,(aq)} \ / \ ClO_{4,(aq)}^{ \  -}$

2. La réaction est totale (simple flèche), l'acide est fort.

Exercice n°14 P 173 : Réaction avec l'eau.

Réaction A : $NH_{3,(aq)} \ + \ H_2O_{(l)} \ \overrightarrow{\longleftarrow} \ NH_{(aq)}^{ \ 4+} \ + \ HO^{ \ -}_{(aq)}$

L'ammoniac $NH_3$ en réagissant avec l'eau $H_2O$, libère un ion hydroxyde $HO^{ \ -}$. Il s'agit d'une base.

La réaction n'étant pas totale, il s'agit d'une base faible.

Réaction B : $CN_{(aq)}^{ \ -} \ + \ H_2O_{(l)} \ \longrightarrow \ HCN_{(aq)} \ + \ HO^{ \ -}_{(aq)}$

L'ion $CN^{ \ -}$ en réagissant avec l'eau $H_2O$, libère un ion hydroxyde $HO^{ \ -}$. Il s'agit d'une base.

La réaction étant totale, il s'agit d'une base forte.

Réaction C : $CH_{3}CO_{2,(aq)}^{ \ -} \ + \ H_2O_{(l)} \ \overrightarrow{\longleftarrow} \ CH_3CO_2H{(aq)} \ + \ HO^{ \ -}_{(aq)}$

L'ion éthanoate $CH_3CO_{2}^{ \ -}$ en réagissant avec l'eau $H_2O$, libère un ion hydroxyde $HO^{ \ -}$. Il s'agit d'une base.

La réaction n'étant pas totale, il s'agit d'une base faible.

Exercice n°16 P 174 : Un acide fort courant.

1. $HCl_{(g)} \ + \ H_2O_{(l)} \ \longrightarrow \ H_{3}O^{ \ +}_{(aq)} \ + \ Cl^{ \ -}_{(aq)}$.

2. Il s'agit d'une solution aqueuse.

3. S'agissant d'un acide fort, la réaction est totale. L'intégralité du chlorure d'hydrogène $HCl_{(g)}$ est passé en solution. La concentration est : $c \ = \ \dfrac{n}{V} \ = \ \dfrac{8,3.10^{ \ -2}}{5,0} \ = \ 1,66.10^{ \ -2} \ mol.L^{ \ -1}$.

4. La réaction étant totale, $\left [H_{3}O^{ \ +}_{(aq)} \right ] \ = \ \left [Cl^{ \ -}_{(aq)} \right ] \ = \ c \ =  1,66.10^{ \ -2} \ mol.L^{ \ -1}$.

5. $pH \ = \ -log \left ( \left [H_{3}O^{ \ +}_{(aq)} \right ] \right ) \ = \ -log \left ( 1,66.10^{ \ -2} \right ) \ = \  1,78$.

Exercice n°17 P 174 : De la soude pour déboucher les canalisations.

1. La solution d'hydroxyde de soude porte son nom des ions la constituant : l'ion hydroxyde $HO^{ \ -}$ et l'ion sodium $Na^{ \ +}$. Une solution étant électriquement neutre, elle est ici constiutée d'autant de charges positives que négatives.

2. S'agissant d'une base forte, elle se dissocie totalement dans l'eau. $ \left [ Na^{ \ +}_{(aq)} \right ] \  =  \ \left [ HO^{ \ -}_{(aq)} \right ]  \ = \ c \ = \ 3,0.10^{ \ -2} \ mol.L^{ \ -1}$.

NB : son $pH$ est : $pH \ = \ -log \left ( \left [ H_3O^{ \ +}_{(aq)} \right ] \right ) \ = \ -log \left ( \dfrac{K_e}{\left [ HO^{ \ -}_{(aq)} \right ]} \right )\ = \ -log  \dfrac{10^{ \ -14}}{3,0.10^{ \ -2}} \ = \ 12,48 $

Exercice n°18 P 174 : Comparer la force des acides.

1. Pour un acide faible se dissociant totalement, on doit avoir : $ \left [ H_3O^{ \ +}_{(aq)} \right ] \ = \ c \ = \ 1,0.10^{ \ -2} \ mol.L^{ \ -1}$, soit : $pH \ = \ -log c = \ 2$.

Le seul vérifiant cette propriété est l'acide sulfamique $H_2NSO_3H$

2. Plus l'acide est fort, plus il se dissociera dans l'eau, plus la concentration en ion $H_3O^{ \ +} $ sera grande, et donc, plus sont pH sera petit.

L'acide sulfamique est plus fort que l'acide chloreux qui est plus fort que l'acide fluorhydrique, qui est plus fort que l'acide hypochloreux.

3. Plus un acide est fort, plus son pKa est petit.

Exercice n°19 P 174 : L'ammoniac.

1.  $c \ = \ \dfrac{n}{V} \ = \ \dfrac{2,5.10^{ \ -3}}{250.10^{ \ -3}} \ = \ 1,0.10^{ \ -2} \ mol.L{ \ -1}$

2.  $\left [ HO^{ \ -}_{(aq)} \right ] \ = \ \dfrac{Ke}{\left [ H_3O^{ \ +}_{(aq)} \right ]} \ = \ \dfrac{10^{ \ -14}}{10^{ \ -10,6}} \ = \ 3,98.10^{ \ -4} \ mol.L^{ \ -1}$

3. 

$$ \begin{array} { | c | c | c | c | c | } Réaction \ : & \ NH_{3(aq)} & + \ H_2O_{(l)} & \overrightarrow{\longleftarrow} & \ NH^{ \ 4+}_{(aq)} & + \ HO^{ \ -}_{(aq)} \\ \hline t_i \ : & n & solvant & & 0 & 0 \\ t \ : & n - x & solvant & & x & x \\ t_f \ : & n - x_f & solvant & & x_f & x_f \\ \end{array} $$

$\tau \ = \ \dfrac{\left [ NH^{ \ 4+}_{(aq)} \right ]}{c} \ = \ \dfrac{\left [ HO^{ \ -}_{(aq)} \right ]}{c} \ = \ \dfrac{3,98.10^{ \ -4}}{1,0.10^{ \ -2}} \ = \ 0,04$

4.  La dissociation n'est pas totale, nous sommes en présence d'une base faible.

Exercice n°22 P 175 : Un acide $\alpha$-aminé.

1.  

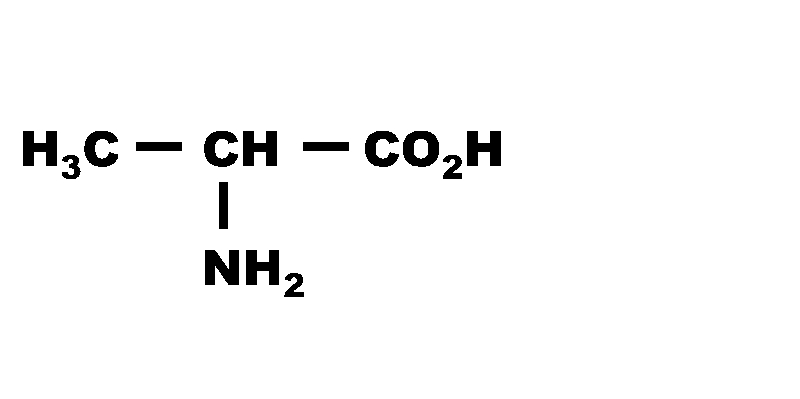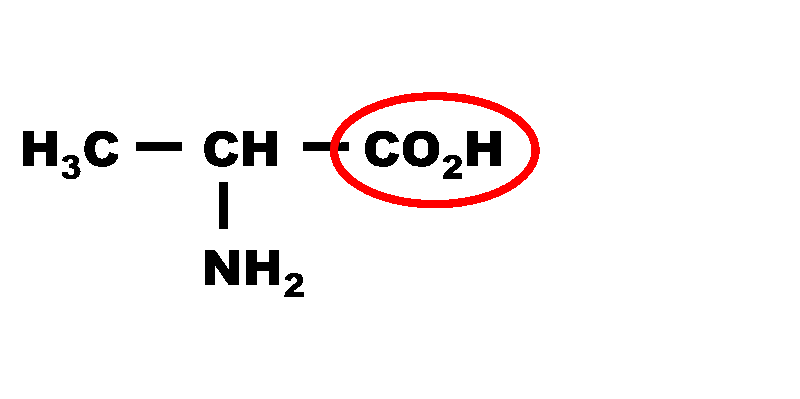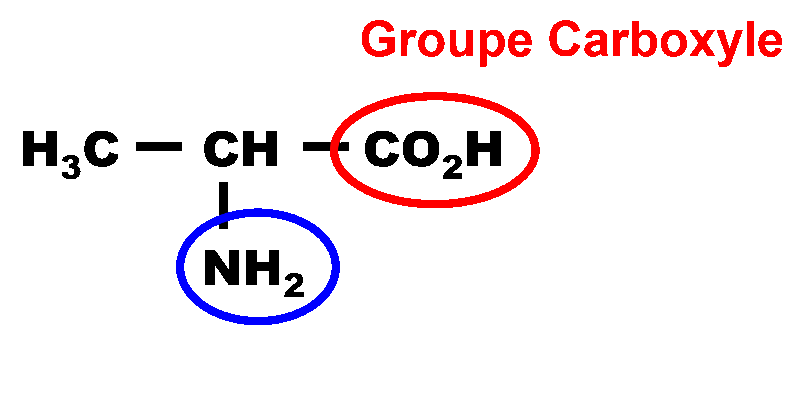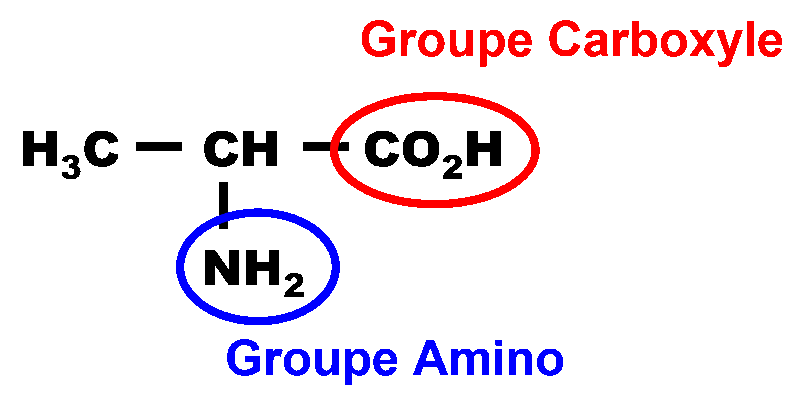
2,3.  Les deux couples sont :

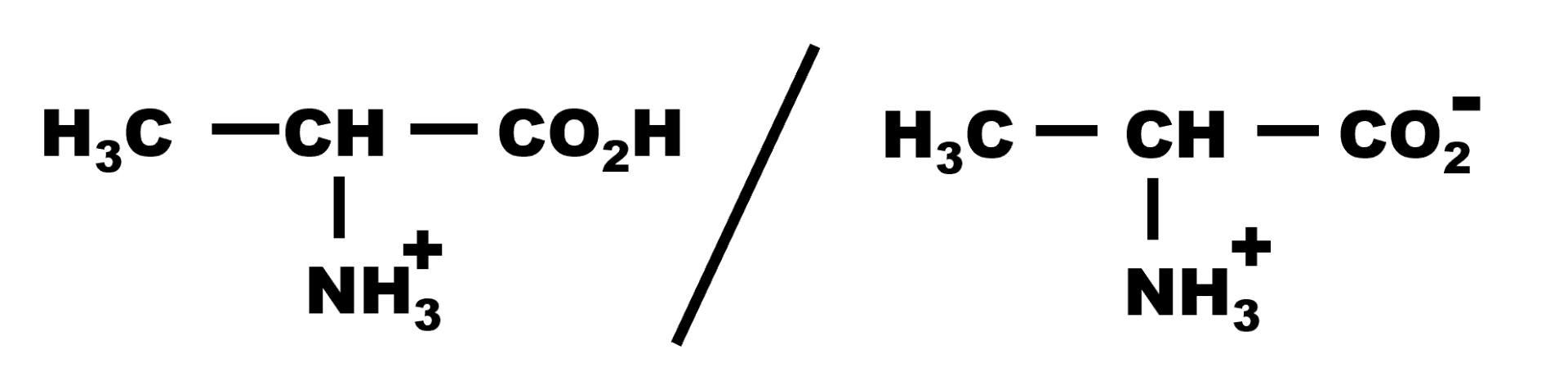	$pK_{A1} \ = \ 2,3$
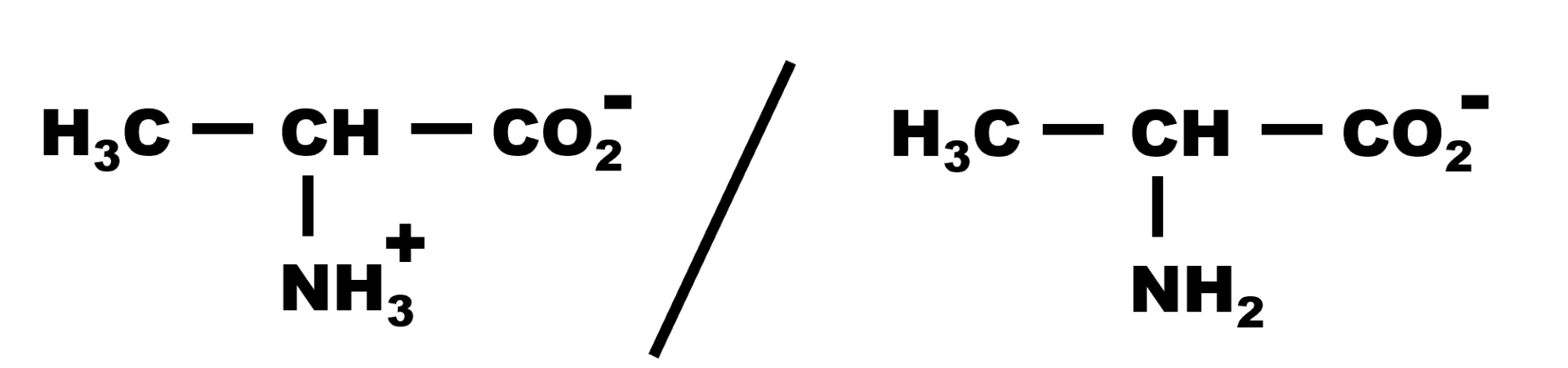	$pK_{A2} \ = \ 9,9$

4.

5. Au-delà d'un pH supérieur à 9,9, la forme qui prédomine est : $H_3C - CH \left ( NH2 \right ) - CO_2^{ \ -}$.

Exercice n°24 P 175 : Choix d'un indicateur coloré.

Pour le premier titrage, le virage se situe pour une valeur de pH entre 6 et 8, l'indicateur approprié sera le bleu de bromothymol qui passera du jaune au bleu.

Pour le deuxième titrage, le virage se situe pour une valeur de pH entre 4 et 6, l'indicateur approprié sera le rouge de méthyl qui passera du jaune au rouge.

Exercice n°26 P 176 : Composition d'une solution d'acide benzoïque.

1.

$$ \begin{array} { | c | c | c | c | c | } Réaction \ : & C_7H_6O_{2(aq)} & + \ H_2O_{(l)} & \overrightarrow{\longleftarrow} & \ C_7H_5O_{2(aq)}^{ \ -} & + \ H_3O^{ \ +}_{(aq)} \\ \hline t_i \ : & n & solvant & & 0 & 0 \\ t \ : & n - x & solvant & & x & x \\ t_f \ : & n - x_f & solvant & & x_f & x_f \\ \end{array} $$

$\left [ C_7H_6O_{2(aq)} \right ] \ = \dfrac{n-x_f}{V} \ = \ c - \dfrac{x_f}{V}$

$\left [ C_7H_5O_{2(aq)}^{ \ -} \right ] \ = \dfrac{x_f}{V} $

$\tau \ = \ \dfrac{ x_f }{c \times V} \ =\dfrac{\left [ C_7H_5O_{2(aq)}^{ \ -} \right ] }{c}$.

On a donc : $\left [ C_7H_5O_{2(aq)}^{ \ -} \right ] \ = \  \left [ H_3O_{(aq)}^{ \ +} \right ] \ = \ \tau \times c$

et $\left [ C_7H_6O_{2(aq)} \right ] \ = \  \ c - \tau \times c$

On a donc : $\fbox{$\left [ C_7H_5O_{2(aq)}^{ \ -} \right ] \ = \ \left [ H_3O_{(aq)}^{ \ +} \right ] \ = \   \tau \times c$}$

et  : $\fbox{$\left [ C_7H_6O_{2(aq)} \right ] \ =  \ c- \tau \times c$}$

2. Le $Ka$ s'écrit : $Ka \ = \ \dfrac{\left [ C_7H_5O_{2(aq)}^{ \ -} \right ] \times \left [ H_3O_{(aq)}^{ \ +} \right ]}{\left [ C_7H_6O_{2(aq)} \right ]}$

$\Leftrightarrow \ \ \fbox{$ \ \ c^2 \tau^2 + Ka. c. \tau -Ka.c \ = \ 0 \ \ $}$

NB : équation du second degré en $\tau$

3. $c^2. \tau^2 + Ka.c. \tau -Ka.c \ = \ 0 \ \ \Leftrightarrow \ \ 4,0.10^{ \ -6}. \tau^2 + 2,0.10^{ \ -7,2}. \tau \ - \ 2,0.10^{ \ -7,2} \ = \ 0$

On trouve alors : $\tau \ = \ 0,16$.

4.

$\left [ C_7H_5O_{2(aq)}^{ \ -} \right ] \ = \tau.c \ = 3,2.10^{ \ -4} \ mol.L^{ \ -1}$

$\left [ H_3O_{(aq)}^{ \ +} \right ] \ \ = 3,2.10^{ \ -4} \ mol.L^{ \ -1} \ \ \Leftrightarrow \ \ pH \ = \ 3,49$

$\left [ C_7H_6O_{2(aq)} \right ] \ = \ c - \tau.c \ = 1,67.10^{ \ -3} \ mol.L^{ \ -1}$

Exercice n°33 P 179 : Composition d'un détartrant.

1a.

$$ \begin{array} { | c | c | c | c | c | } Réaction \ : & CH_3CO_2H_{(aq)} & + \ H_2O_{(l)} & \overrightarrow{\longleftarrow} & \ CH_3CO_{2(aq)}^{ \ -} & + \ H_3O^{ \ +}_{(aq)} \\ \hline t_i \ : & n & solvant & & 0 & 0 \\ t \ : & n - x & solvant & & x & x \\ t_f \ : & n - x_f & solvant & & x_f & x_f \\ \end{array} $$

$\tau \ = \ \dfrac{ x_f }{c \times V} \ = \ \dfrac{\left [ CH_3CO_{2(aq)}^{ \ -} \right ] }{c} \ = \ \dfrac{\left [ H_3O_{(aq)}^{ \ +} \right ]}{c} $

$\left [ CH_3CO_{2(aq)}^{ \ -} \right ] \ = \ \left [ H_3O_{(aq)}^{ \ +} \right ] \  = \ \tau \times c $

$\left [ C_3CO_2H_{(aq)} \right ] \ = \dfrac{n-x_f}{V} \ = \ c - c \times \tau$

1b. Le $Ka$ s'écrit : $Ka \ = \ \dfrac{\left [ CH_3CO_{2(aq)}^{ \ -} \right ] \times \left [ H_3O_{(aq)}^{ \ +} \right ]}{\left [ CH_3CO_2H_{(aq)} \right ]}$.

Soit : $Ka. \left ( c- \tau.c \right) \ = \ c^2. \tau^2$.

$\Leftrightarrow \ \ Ka.c - \tau.c.Ka - c^2. \tau^2 \ = \ 0$.

$\Leftrightarrow \ \ c.\tau^2 + Ka. \tau - Ka \ = \ 0$. (CQFD)

2a. L'équation s'écrit : $8,0.10^{ \ -2}.\tau + 10^{ \ -4.8} \tau - 10^{ \ -4,8} \ = 0$.

En résolvant cette équation du sencond degré, on trouve : $\tau \ =  \ 1,40.10^{ \ -2}$.

$\left [ CH_3CO_{2(aq)}^{ \ -} \right ] \ = \tau.c \ = 1,12.10^{ \ -3} \ mol.L^{ \ -1}$

$\left [ H_3O_{(aq)}^{ \ +} \right ] \ \ = 1,12.10^{ \ -3} \ mol.L^{ \ -1} \ \ \Leftrightarrow \ \ pH \ = \ 2,95$

$\left [ CH_3CO_2H_{(aq)} \right ] \ = \ c - \tau.c \ = 7,90.10^{ \ -2} \ mol.L^{ \ -1}$

2b. La valeur mesuré est cohérente avec celle calculée.

Exercice n°36 P 179 : Diagramme de distribution.

1. La ligne 4 demande la valeur du pKa.

Le "float" convnertit la suite de caractères en un nombre.

2. La grandeur tracée en abscisse est le pH : plt.xlabel("pH") à la ligne 12.

3a. La grande alpha(pH) correspond au pourcentage d'acide AH. (ligne 10)

3b. La couleur est le rouge : "r". (ligne 10)

3c. L'acide $AH$ se dissociant, la concentration initiale $c$ est égale à la somme des concentrations en $AH$ présent est $A^{ \ -}$ présent.

$c \ = \ \left [ AH \right ] + \left [ A^{ \ -} \right ]$ (1)

Comme $K_a \ = \ \dfrac{\left [ H_3O^{ \ +} \right ] \times \left [ A^{ \ -} \right ]}{\left [ AH \right ]}$

Donc : $\left [ A^{ \ -} \right ] \ = \ \dfrac{ K_a \times \left [ AH \right ] }{\left [ H_3O^{ \ +} \right ]}$

En reportant dans l'expression (1) :

$$c \ = \ \left [ AH \right ] \ + \ \dfrac{ K_a \times \left [ AH \right ] }{\left [ H_3O^{ \ +} \right ]} $$
$$\Leftrightarrow \ c \ = \left [ AH \right ] \times \left ( 1+ \dfrac {K_a}{\left [ H_3O^{ \ +} \right ]} \right ) $$
$$\Leftrightarrow \ c \ = \ \left [ AH \right ] \times \left ( \dfrac{ \left [ H_3O^{ \ +} \right ] + K_a}{\left [ H_3O^{ \ +} \right ]} \right )$$.

Le pourcentage en $AH$ ramené à la concentration initiale $c$ est donc : 

$$100 \times \dfrac {\left [ AH \right ]}{c} \ = \ 100 \times \dfrac{\left [ H_3O^{ \ +} \right ]}{ \left [ H_3O^{ \ +} \right ] + K_a} $$

$$100 \times \dfrac {\left [ AH \right ]}{c} \ = \ 100 \times \dfrac{10^{ \ -pH}}{10^{ \ -pH} + 10^{ \ -pK_a}} $$