Gaz Parfaits

Exercice n°13 P385 : Mélange de deux gaz.

1a.

La vitesse des particules est plus grande dans le récipient à la température $T_1$. L'agitation thermique est plus grande. La température est supérieure à celle du deuxième récipient.

1b.

On dénombre la même quantité de molécules dans les deux enceintes qui ont le même volume. La masse volumique est donc la même.

2a.

A l'état d'équilibre, l'agitation thermique sera la même dans toute l'enceinte, les particules se déplaceront aléatoirement dans tous les sens à la même vitesse.

2b.

Les particules étant les mêmes, elles se transferent la chaleur par contact (conductivité thermique).

2c.

$T_2 \ < \ T \ < T_1$.

Exercice n°14 P385 : Masse volumique de l'air.

1a.

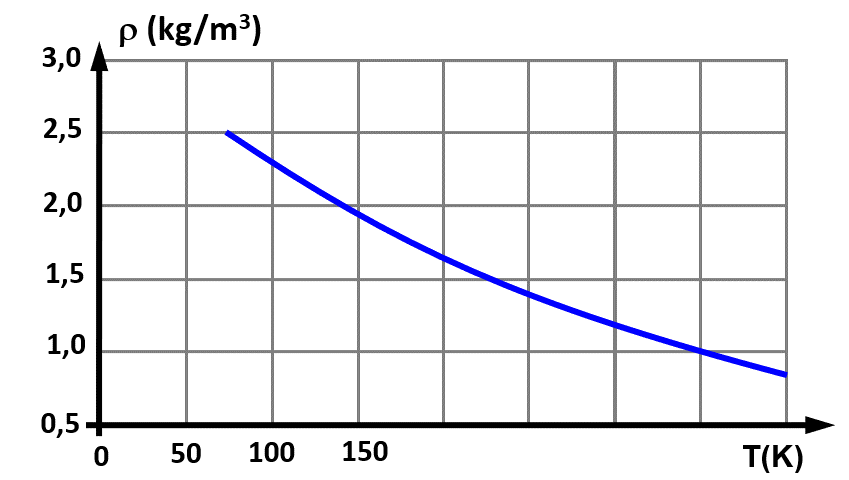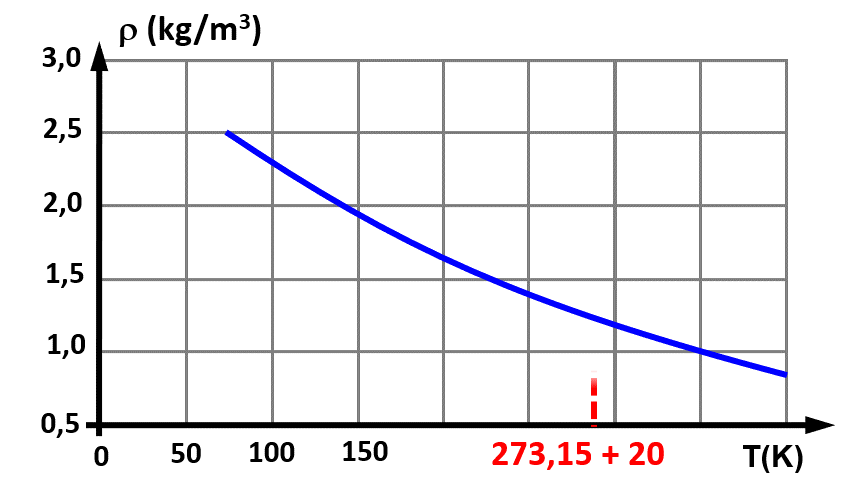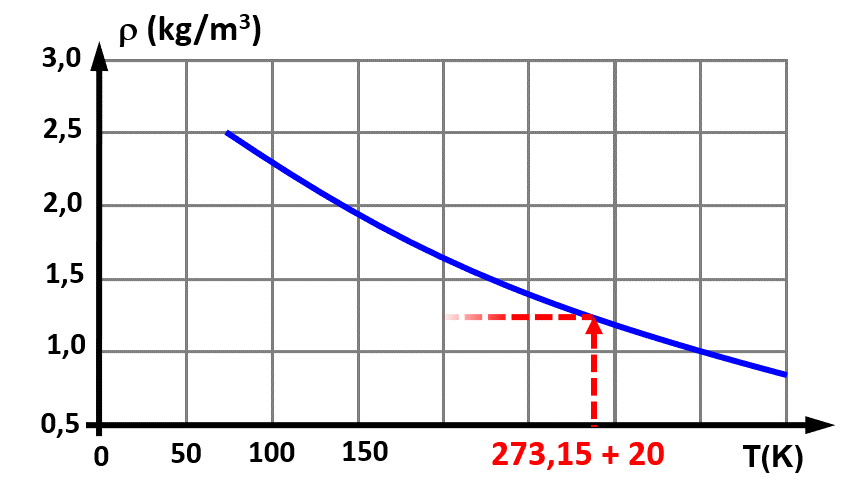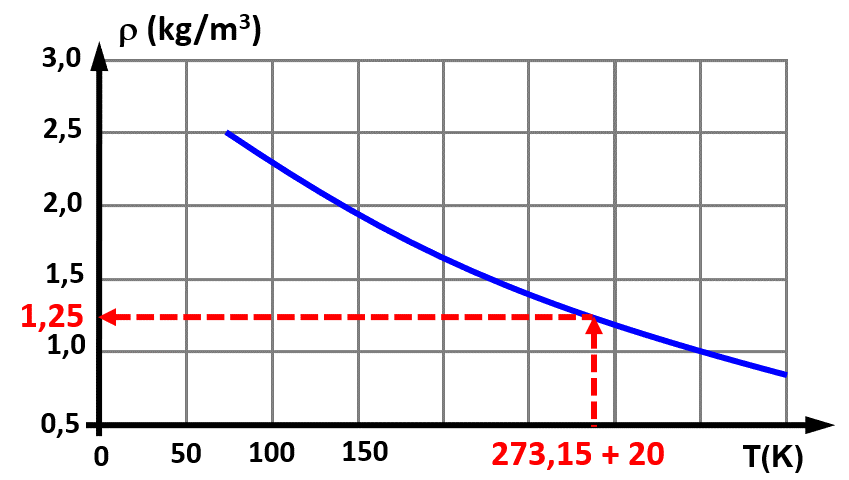
A 20°C, $T \ = \ 273,15 + 20 \ = 293,15 \ K$, on détermine une masse volumique : $\rho_{293} \ = \ 1,25 \ kg.m^{ \ -3}$

1b.

La température d'ébullition de l'air est $\theta_{eb} \ -194,3 \ °C$ soit : $T \ = \ -194,3 + 275,13 \ = \ 78,9 \ K$. En dessous de cette température, l'air n'est pas un gaz, mais un liquide.

2a.

ELa température absolue (en Kelvin) ne peut pas être négative.

2b.

Plus la température augmente, plus elles sont agitées et se déplacent de plus en plus, elles occupent un volume de plus en plus grand.

Exercice n°15 P386 : Comportement du gaz parfait.

Pour un gaz parfait : $PV \ = \ nRT$.

1a.

D'après l'équation d'état, le produit $PV$, à température constante augmente avec la quantité de matière.

1b.

L'équation d'état du gaz parfait est un modèle applicable à tout gaz considéré comme parfait, il est indépendant de la nature du gaz considéré comme tel.

2.

La pression $P$ s'exprime en Pascals $(Pa)$, le volume $V$ en mètres cube $(m^3)$, la quantité de matière $n$ en moles $(mol)$, la temprature T en Kelvin $(K)$. La constante $R$ s'exprime en Joule par kilogramme par Kelvin ($J.kg^{ \ -1}.K^{ \ -1}$).

3a.

$P \ = \ \dfrac{nRT}{V}$, donc, à volume constant, si la température augmente, la pression augmente.

3b.

$P \ = \ \dfrac{nRT}{V}$, donc, à température constante, si le volume diminue, la pression augmente.

Exercice n°17 P386 : Comportement du gaz parfait.

Pour un gaz parfait : $PV \ = \ nRT$.

1.

$V \ = \ \dfrac{nRT}{P} \ = \ \dfrac{1,5.10^{ \ -2} \times 8,31 \times 293,15}{1,013.10^{5}} \ = \ 3,61.10^{ \ -4} \ m^3$ soit : $0,36 \ L$

2a.

A pression constante, si la température augmente, le volume augmente.

2b.

A température constante, si la pression diminue, le volume augmente.

2c.

A température et pression constantes, le volume reste constante quelque soit le gaz considéré comme parfait.

Exercice n°18 P386 : Ballon de baudruche.

1.

$PV \ = \ nRT \ \Leftrightarrow n \ = \ \dfrac{PV}{RT} \ = \ \dfrac{1,1 \times 1,013.10^{ \ 5 } \times 2,0.10^{ \ -3}}{8,31 \times 298} \ = \ 9,0.10^{ \ -2} \ mol$.

2a.

$P \ = \ \dfrac{nRT}{V} \ = \ \dfrac{9,0.10^{ \ -2} \times 8,31 \times 298}{3,0 \times 10^{ \ -3}} \ = \ 7,43 \ Pa$

2b.

$T \ = \ \dfrac{PV}{nR} \ = \ \dfrac{1,1 \times 1,013.10^{ \ 5} \times 3,0.10^{ \ -3}}{9,0.10^{ \ -2} \times 8,31} \ = \ 447 \ K$ soit 174 °C

2c.

$n_f \ = \ \dfrac{PV}{RT} \ = \ \dfrac{1,1 \times 1,013.10^{ \ 5} \times 3,0.10^{ \ -3}}{298 \times 8,31} \ = \ 1,35.10^{ \ -1} \ mol$

Il faut donc rajouter : $1,35.10^{ \ -1} - 9,0.10^{ \ -2} \ = \ 4,45.10^{ \ -2} \ mol$

Soit une masse de : $m \ = \ n \times M \ = 4,45.10^{ \ -2} \times 4,0 \ = \ 0,18 \ g$

Exercice n°20 P386 : Gonflage d'un ballon.

1.

Lors de la première phase, l'air dispose de l'espace nécessaire sans subir aucune contrainte. La pression est constante ainsi que la masse volumique (semblable à celle de l'extérieur).

Lors de la seconde phase, la quantité d'air est de plus en plus importante pour un volume constant (celui du ballon). La masse volumique augmente, ainsi que la pression.

2.

Equation d'état : $P \times V \ = \ n \times R \times T$. Masse volumique : $\rho \ = \ \dfrac{m}{V}$.

On en déduit : $P \ = \ \dfrac{RT}{M} \times \rho$

Première phase : la masse volumique ne changeant pas, la pression non plus.

Deuxième phase : la masse volumique augmentant, la pression augmente porportionnelement.

Exercice n°21 P387 : Volume molaire.

1a.

$\rho \ = \ \dfrac{m}{V} \ \Leftrightarrow \ V \ = \ \dfrac{m}{\rho} \ = \ \dfrac{1,6.10^{ \ -3}}{\ 2,0} \ = \ 8,0.10 ^{ \ -4} \ m^{ \ 3}$

1b.

$n \ = \ \dfrac{PV}{RT} \ = \ \dfrac{1,013.10^{ \ 5} \times 8,0.10^{ \ -4}}{8,31 \times 293} \ = \ \ 3,33.10^{ \ -2} \ mol$

1c.

$V_m \ = \ \dfrac{V}{n} \ = \ \dfrac{8,0.10^{ \ -4}}{ 3,33.10^{ \ -2 }} \ = 0,024 \ m^{ \ 3}.mol^{ \ -1 }$ soit $ 24 \ L.mol^{ \ -1}$

1d.

Pour tout gaz parfait, le volume molaire dépend de la température.

$V \ = \ \dfrac{nRT}{P} \ \Leftrightarrow \ V_m \ = \dfrac{RT}{P} \ = \ \dfrac{8,31 \times 263}{1,013.10^{ \ 5}} \ = \ 21,6.10^{ \ -2} \ m^{ \ 3}$ soit : $21,6 \ L$.

2.

A 20°C :

$\rho_{but} \ = \ \dfrac{m}{V} \ \Leftrightarrow \ V \ = \ \dfrac{m}{\rho} \ = \ \dfrac{1,6.10^{ \ -3}}{\ 2,7} \ = \ 5,9.10 ^{ \ -4} \ m^{ \ -3}$

$n_{but} \ = \ \dfrac{PV}{RT} \ = \ \dfrac{1,013.10^{ \ 5} \times 5,9.10^{ \ -4}}{8,31 \times 293} \ = \ 2,47.10^{ \ -2} \ mol$

$V_{m,but} \ = \ \dfrac{V}{n} \ = \ \dfrac{5,9.10^{ \ -4}}{ 2,47.10^{ \ -2 }} \ = 0,024 \ m^{ \ 3}.mol^{ \ -1 }$ soit $ 24 \ L.mol^{ \ -1}$

On retrouve la même valeur... logique, les deux gaz étant considérés comme parfaits, cette dernière valeur est la même quel que soit le gaz parfait.

A -10°C, le butane est liquide, ce n'est pas un gaz. On ne peut plus appliquer la loi des gaz parfaits.

Exercice n°22 P387 : Validité du gaz parfait.

1.

$P_{atm} \times V_{atm} \ = \ P \times V$. Cette loi est valide à température identique.

2a.

$P_1 \ = \ \dfrac{P_{atm} \times V_{atm}}{V_1} \ = \ \dfrac{1,021.10^{5} \times 18}{6} \ = 3,063.10^{5} \ Pa$

$P_2 \ = \ \dfrac{P_{atm} \times V_{atm}}{V_1} \ = \ \dfrac{1,021.10^{5} \times 18}{2} \ = 9,189.10^{5} \ Pa$

2b.

La première valeur correspond à la valeur calculée. La seconde aussi.

Exercice n°24 P388 : Réaction explosive.

1a.

D'après la réaction, pour 4 moles de trinitroglycérine, on obtient $12 + 10 + 6 + 1 = 29 \ moles$ de gaz parfait.

Pour $7,0.10^{ \ -2} \ mole$ de trinitroglycérine, on obtient donc : $\dfrac{7,0.10^{ \ -2} \times 29}{4} \ = 5,08. 10^{ \ -1} \ mole$ de gaz parfait.

La pression correspondante est : $P \ = \ \dfrac{5,08.10^{ \ -1} \times 8,31 \ 293,15}{10,0.10^{-6}} \ = 1,24. 10^{ \ 8} \ Pa$

1b.

$T \ = \ \dfrac{PV}{nR}$. A volume constant, un accroissement de pression entraîne de facto une augmentation de température $\Delta T \ = \ \dfrac{V}{nR} \Delta P$

2a.

$V \ = \ n \times V_m \ = \ 5,08.10^{ \ -1} \times 24,0 \ = 12,2 \ L$

Le volume est $ \dfrac{12,2}{10.10^{ \ -3}} \ = \ 1220 $ fois plus important.

2b.

A l'échelle microscopique : au départ, la trinitroglycérine liquide. Se transformant en gaz, les molécules produites 7 fois plus nombreuses que les molécules de liquide, les chocs sur les parois du contenant sont beaucoup plus importantes, d'où l'explosion.

Exercice n°26 P389 : Loi d'Avogadro-Ampère.

On rappelle la loi des gaz parfaits : $PV \ = \ nRT$.

1.

D'après la loi des gaz parfaits : $n \ = \ \dfrac{PV}{RT}$

Quel que soit le gaz parfait, si $P$, $V$, et $T$ sont les les mêmes, la quantité de matière $n$ est la même.

2a.

$V_m \ = \ \dfrac{RT}{P} \ = \ \dfrac{8,31 \times 293,15}{1,013.10^{ \ 5}} \ = \ 24,0.10^{ \ -2} \ m^3$ soit $24,0 \ L$

2b.

Etant le même, quelque soit le gaz considéré comme parfait : $V_m(CO_2) \ = \ 24,0 \ L$

2c.

Il s'agit du volume MOLAIRE, c'est-à-dire celui d'une mole de gaz parfait : $24,0 \ L$

3a.

Le volume molaire précédent $V_m \ = \ \dfrac{RT}{P}$ est celui déterminé à $20°C$. A une températuree plus basse, les molécules sont moins agitées, le volume molaire sera plus petit.

3b.

$V_m(0°C) \ = \ \dfrac{RT}{P} \ = \ \dfrac{8,31 \times 273,15}{1,013.10^{ \ 5}} \ = \ 22,4.10^{ \ -2} \ m^3$ soit $22,4 \ L$ est celui déterminé à $20°C$. A une températuree plus basse, les molécules sont moins agitées, le volume molaire sera plus petit.

Exercice n°27 P389 : Masse volumique d'un gaz parfait.

1a.

$\rho \ = \ \dfrac{m}{V}$ or : $PV \ = \ nRT$ donc : $\rho \ = \ \dfrac{mP}{nRT} \ = \ \dfrac{MP}{RT}$

1b.

A pression constante, la masse volumique diminue avec la température.

A température constante, la masse volumique augmente avec la pression.

1c.

A pression constante, l'agitation moléculaire diminue avec la température. Pour une même température, on trouvera moins de molécules dans un même volume, ce qui implique une diminution de la masse volumique.

A température constante, l'agitation moléculaire augmente avec la pression. Pour une même pression, on trouvera plus de molécules dans un même volume, ce qui implique une augmentation de la masse volumique.

2a.

$\rho_{air} \ = \ = \dfrac{28,9.10^{ \ -3} \times 1,013.10^{ \ 5}}{8,31 \times 293,15} \ = \ 1,2 \ kg.m^{ \ -3}$

2b.

$\rho_{Everest} \ = \ = \dfrac{28,9.10^{ \ -3} \times 0,3 \times 1,013.10^{ \ 5}}{8,31 \times 233,15} \ = \ 0,45 \ kg.m^{ \ -3}$

3.

La masse molaire de l'hélium étant plus faible que celle de l'air, il en ira de même de sa masse volumique. Les valeurs deront divisées par $\dfrac{28,9}{4,0} \ = 7,23$