Les Systèmes Electriques

Exercice n°15 P 510 : Différence de phase.

A.		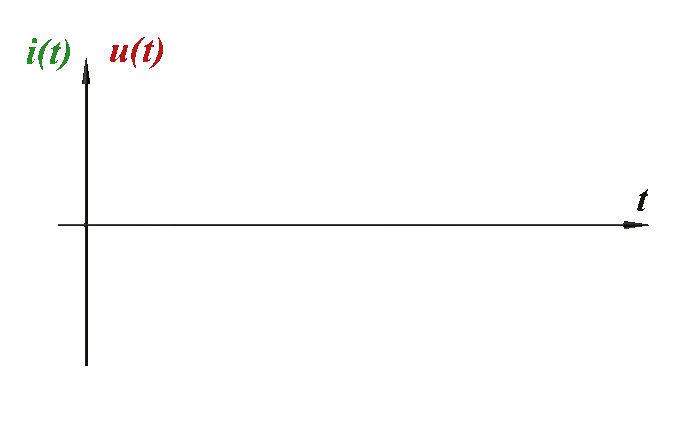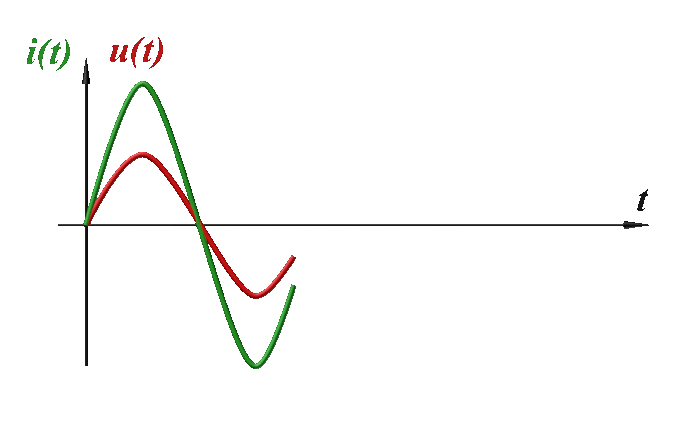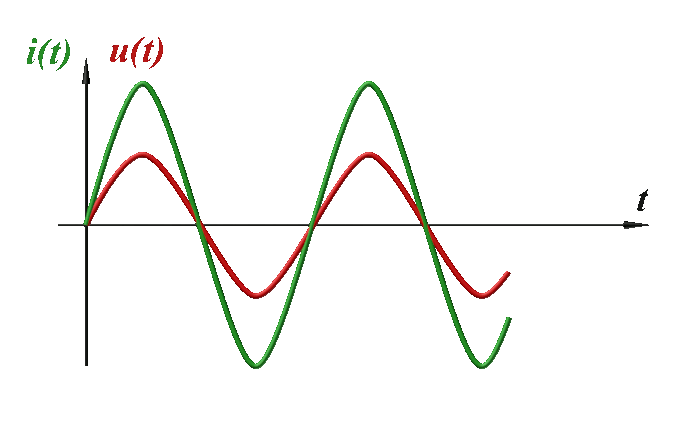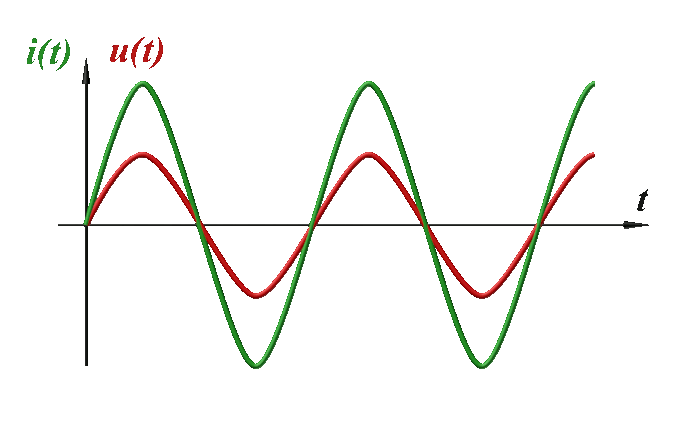L'intensité $i(t)$ et la tension $u(t)$ sont en phase
B.		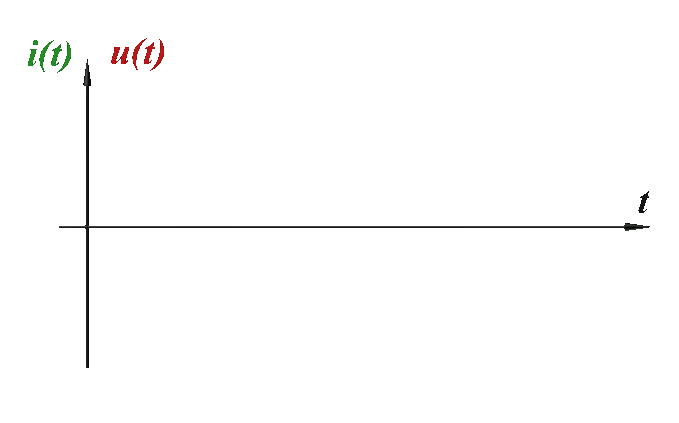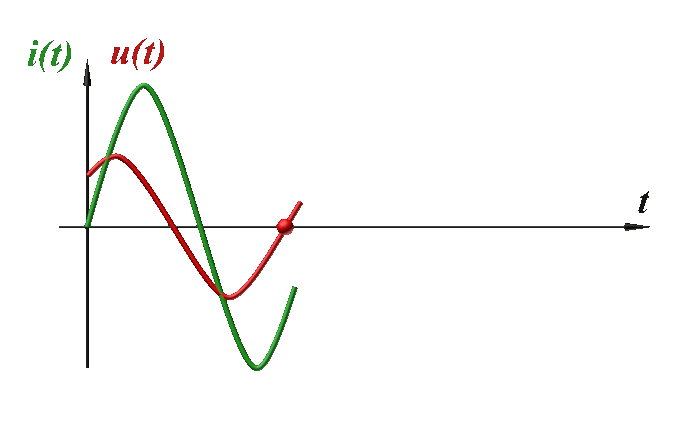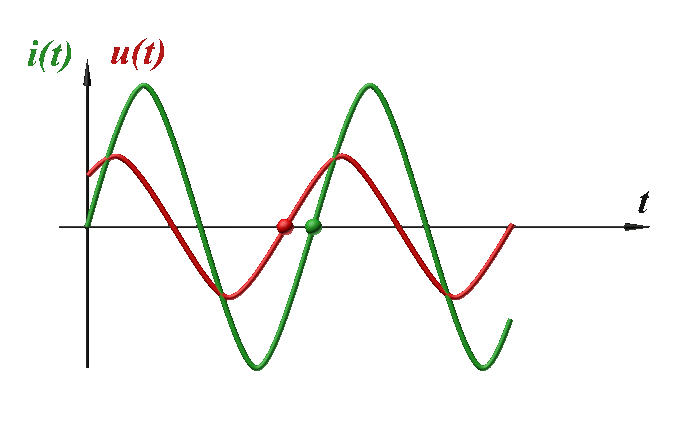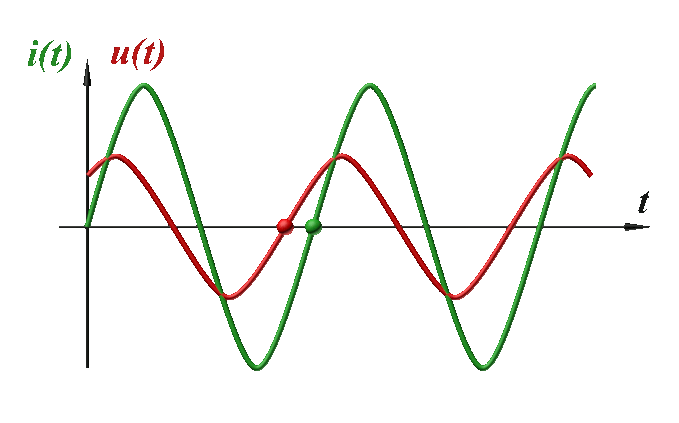Dans une même situation (annulation au centre), la tension $u(t)$ l'atteint avant l'intensité $i(t)$. Elle est en avance. Le dipôle n'a donc pas un comportement capacitif.
C.		Les deux signaux sont en opposition de phase quand l'une atteint son maximum, l'autre atteint son minimum, et inversement.

Exercice n°16 P 510 : Comportement capacitif.

1.

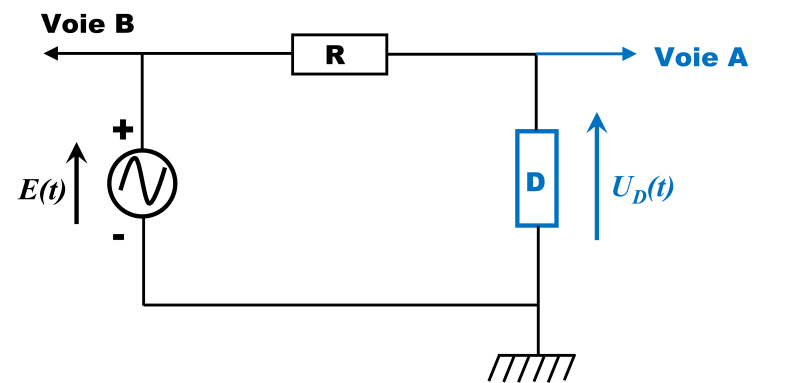
2.

L'intensité est en retard sur la tension. Le dipôle n'a pas un comportement capacitif.

Exercice n°20 P 511.

1.

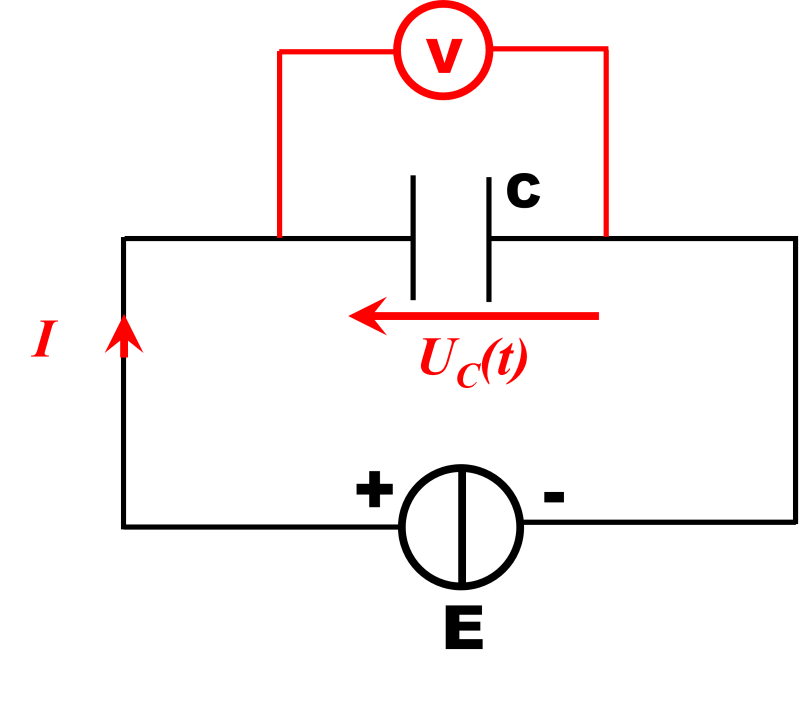
2a.

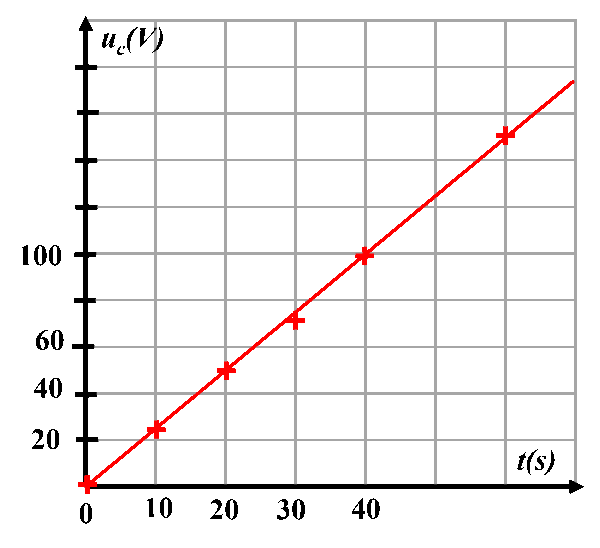
2b.

La tension aux bornes du condensateur est proportionnelle au temps.

2c.

La charge du condensateur $q(t)$ est proportionnelle à la tension à ses bornes :$q(t)= \ \ u_c(t)$.

La charge du condensateur $q(t)$ est proportionnelle à sont temps de charge et au courant $I \ : \ q(t)= \ = \ I \times \Delta t$.

Donc : $u_(c) \ = \ \dfrac{I}{C} \times \Delta t$

Le coefficient directeur de la droite est donc :$ \dfrac{I}{C} \ = \ \dfrac{1,0.10^{ \ -3}}{C} \ = \ \dfrac{152}{60}$

On en déduit : $C \ = \ \dfrac{1,0.10^{ \ -3} \times 60}{152} \ = \ 3,9.10^{ \ -4} \ F$

Exercice n°22 P 511 : Tension aux bornes d'un condensateur.

$u_C(t) \ = \ E. \left ( 1 \ - e^{ \ - \ \dfrac{t}{RC}} \right )$

1.

$u_C(t)$ : tension aux bornes du condensateur, en volts (V)

$E$ : tension aux bornes du générateur, en volts (V)

$R$ : résistance du résistor en ohmd ($\Omega$)

$C$ : vapacité du condensateur en farads (F)

2a.

La tension $u_C(t)$ aux bornes du condensateur dépend du temps, car sa charge $q(t)$ n'est pas instantanée.

2b.

Quand $t$ tend vers l'infini, le terme $- \ \dfrac{t}{RC}$ tend vers $-\infty$, l'exponentielle tend vers $0$.

Le terme $1 \ - e^{ \ - \ \dfrac{t}{RC}}$ tend vers $1$.

Le terme $u_C(t)$ tend vers $E$.

3.

Dans cette expression, $u_C(t)$ est croissante, le condensateur est en charge.

Exercice n°23 P 511 : Charge d'un condensateur.

1.

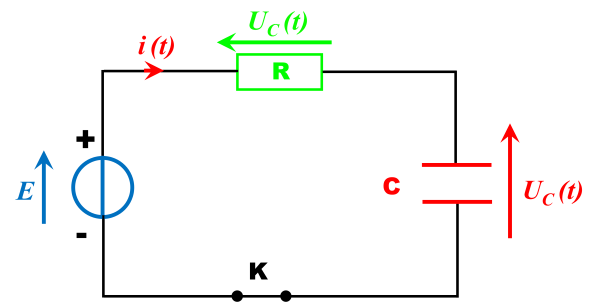
2a.

A l'instant initial, le condensateur n'étant pas chargé, la tension $u_C(t) \ = \ C \times q(t)$ est nulle.

2b.

Une fois le condensateur chargé, la tension à ses bornes sera égale à $E$.

3.

D'après la loi des mailles : $\color{blue}{E} \ = \ \color{green}{u_R(t)} \ + \ \color{red}{u_C(t)}$.

La tension aux bornes du résistor est : $\color{green}{u_R(t)} \ = \ R \times i(t)$.

L'intensité est : $i(t) \ = \ \dfrac{dq(t)}{dt}$.

Donc : $\color{green}{u_R(t)} \ = \ R \times \dfrac{dq(t)}{dt}$.

La charge du condensateur est : $q(t) \ = \ C \times \color{red}{u_C(t)}$.

Alors : $\color{green}{u_R(t)} \ = \ R \ \times C \times \color{red}{\dfrac{{du_C(t)}}{dt}}$.

Finalement : $\color{blue}{E} \ = \ R \ \times C \times \color{red}{\dfrac{{du_C(t)}}{dt}} \ + \color{red}{u_C(t)}$.

4.

$u_C(t) \ = \ A \ + \ B \times e^{ \ - \ \dfrac{t}{RC}}$

A $t\ = \ 0 \ , \ u_C(0) \ = 0 \ = \ A \ + \ B \ \ \ \Leftrightarrow \ \ \ A \ = \ - \ B$

A $t\ = \ + \ \infty \ , \ u_C(\infty) \ = E \ = \ A$

Donc : $u_C(t) \ = \ E \ - \ E \times e^{ \ - \ \dfrac{t}{RC}} \ = \ E \times \left ( 1 \ - \ e^{ \ - \ \dfrac{t}{RC}} \right )$

5.

$\dfrac{du_C(t)}{dt} \ = \ + \ \dfrac{E}{RC} \times e^{ \ - \ \dfrac{t}{RC}}$

Donc : $RC \times \dfrac{u_C(t)}{dt} \ + \ u_C(t) = \ E \times e^{ \ - \ \dfrac{t}{RC}} \ + \ E \times \left ( 1 \ - \ e^{ \ - \ \dfrac{t}{RC}} \right ) \ = \ \color{red}{E \times e^{ \ - \ \dfrac{t}{RC}}} \ + \ E \times 1 \ - \color{red}{E \ \times \ e^{ \ - \ \dfrac{t}{RC}}}$

Soit : $\color{red}{u_C(t)} \ + \ \color{green}{u_R(t)}= \ \color{blue}{E}$, CQFD

Exercice n°24 P 512 : Décharge d'un condensateur.

1a.

$u_R(t) \ = \ R \color{blue}{\times i(t)} \ \ \Leftrightarrow \ \ \color{blue}{\times i(t)} \ = \ - \ \dfrac{dq(t)}{dt} \ = \ - \dfrac{1}{R} \times u_R(t)$ (le condenstateur est en décharge).

$\color{blue}{i(t)} \ = \ C \times \dfrac{du_C(t)}{dt}$.

1b.

Le courant $i(t)$ est le même en tout point d'un circuit série.

Donc : $ \dfrac{1}{R} \times u_R(t) \ = \ - \ C \times \dfrac{du_C(t)}{dt} \ \ (1)$.

La tension aux bornes du condensateur et du résistor montés en dérivation est la même : $u_R() \ = \ u_R(t)$.

Donc, en reportant dans $(1) \ \ : \ \ \dfrac{1}{R} \times u_C(t) \ = \ - \ C \times \dfrac{du_C(t)}{dt}$

Soit : $\dfrac{du_C(t)}{dt} \ = \ - \ \dfrac{1}{RC} \times u_C(t) \ \ \Leftrightarrow \color{red}{\dfrac{du_C(t)}{dt} \ + \ \dfrac{1}{RC} \times u_C(t) \ = \ 0}$

2.

Si $u_C(t) \ = \ E \times e^{- \dfrac{t}{RC}} \ \ : \ \ \dfrac{du_C(t)}{dt} \ = \ - \dfrac{E}{RC} \times \ e^{- \dfrac{t}{RC}}$

En reportant dans l'équation différentielle précédente : $- \dfrac{E}{RC} \times \ e^{- \dfrac{t}{RC}} + \dfrac{E}{RC} \times \ e^{- \dfrac{t}{RC}} = \ 0$ : CQFD

Exercice n°25 P 512 : Réponse d'un circuit RC.

1.

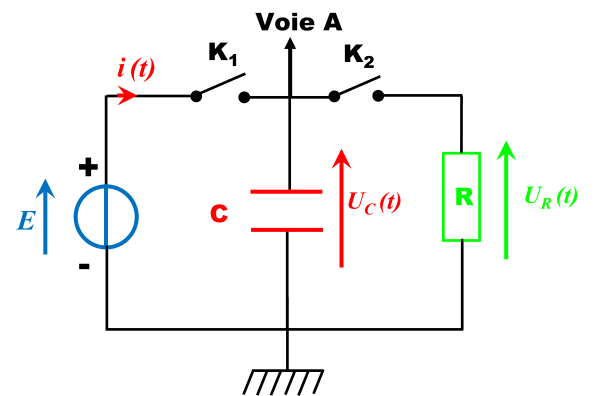
2a.

La tension Délivrée par le condensateur est la tension maximale q'atteint la tension aux bornes de condensateur : $E \ = \ 3 \ V$.

2b.

La courbe correspondant à la charge du condensateur est $\color{green}{u_2(t)}$.

La courbe correspondant à la décharge du condensateur est $\color{blue}{u_2(t)}$.

3a.

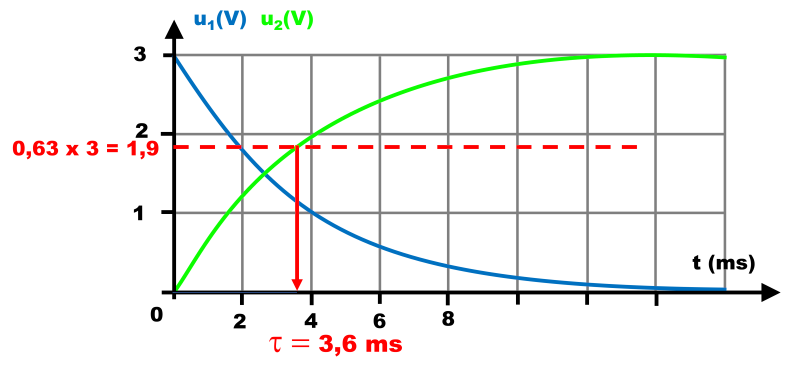
3b.

La valeur attentdue est $\tau \ = \ R \times C \ = \ 330 \times 12.10^{ \ -6} \ = \ 4,0.10^{ \ -3} \ s$. Cohérenté avec la valeur déterminée graphiquement.

Exercice n°29 P 514 : Décharge d'un condensateur et temps caractéristique.

1.

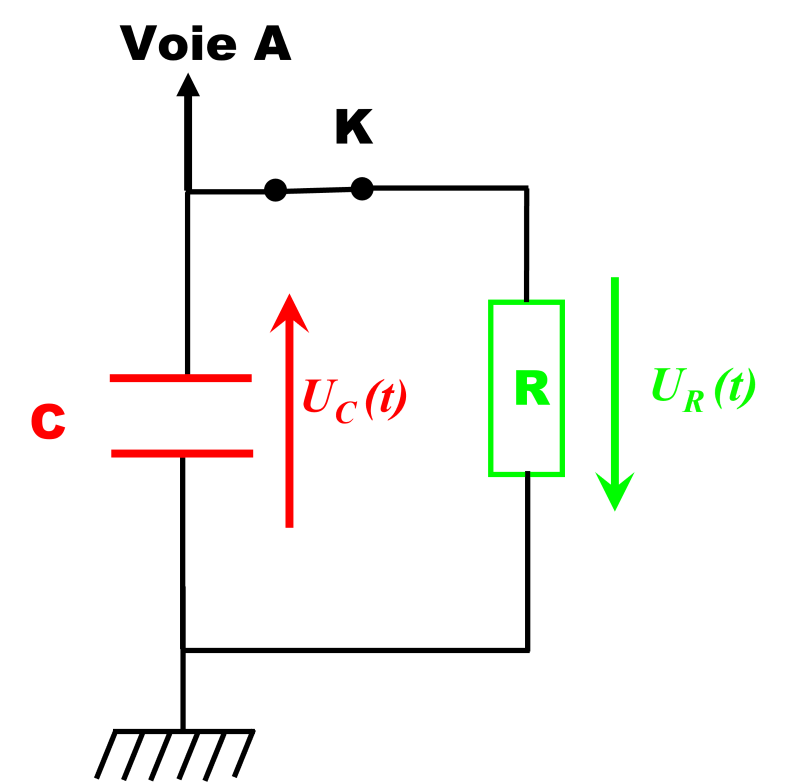
2.

$u_R(t) \ + \ u_C(t) \ = \ 0$

Or : $u_R(t) \ = \ R \times i(t), \ i(t) \ = \ \dfrac{q(t)}{dt} \ et \ q(t) \ = \ C \times u_C(t)$

Donc : $RC \dfrac{du_C(t)}{dt} \ + \ u_C(t) \ = \ 0$

3a.

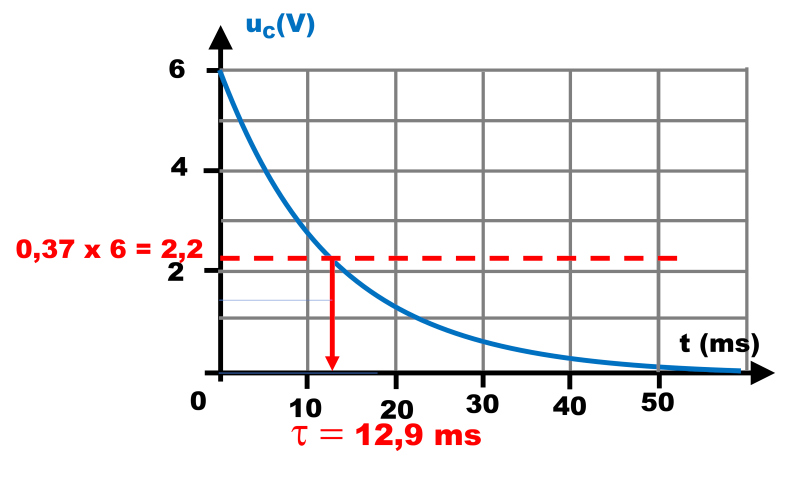
3a.

$\tau \ = R \times C \ = 500 \times C\ 12,9 \ ms$

Donc : $C \ = \ \dfrac{12,9.10^{ \ -3}}{500} \ = R \times C \ = \ 2,6.10^{ \ -5} \ F$.

Exercice n°29 P 514 : Décharge d'un condensateur et temps caractéristique.

1.

Voir exercice précédent.

2.

$\dfrac{du_C(t)}{dt} \ + \dfrac{1}{\tau} \times \ u_C(t) \ = \ 0$

Le terme $\dfrac{du_C(t)}{dt}$, rapport d'une tension à un temps s'exprime en $V.s^{ \ -1}$

Le terme $\dfrac{1}{\tau} \times \ u_C(t)$ doit donc être de la même dimension : $V.s^{ \ -1}$

$u_C(t)$ étant une tension (en volts V), terme $\tau$ est donc homogène à un temps.

3a.

$u_C(t) \ = \ U_0 \times e^{ \ -t/ \tau}$ donc : $\dfrac{u_C(t)}{dt} \ = \ U_0 \times \dfrac{-1}{\tau} \times e^{ \ -t/ \tau}$

Alors : $\dfrac{du_C(t)}{dt} \ + \dfrac{1}{\tau} \times \ u_C(t) \ = \ -U_0 \times \dfrac{1}{\tau} \times e^{ \ -t / \tau} \ + \ \dfrac{1}{\tau} \times U_0 \times e^{ \ -t/ \tau} \ = \ 0$ CQFD.

3b.

Pour $t \ = \ 5 \times \tau \ : \ u_C(5 \tau) \ = U_0 \times e^{ \ -5} \ = 6,7.10^{ \ -5} U_0 \ \cong 0$.

4.

$ 5 \times \tau \ = \ 5 \times RC \ = \ 5 \times 220 \times 1,0 \ = \ 1100 \ s$ soit $18 \ min \ 33 \ s$