Lunette astronomique

Exercice n°13 P 465 : L'association correcte.

1,2.

La bonne association correspondant à la lunette afocale est la première.

Il faut que le foyer image de l'objectif corresponde avec le foyer objet de l'oculaire, de sorte que l'image finale soit une image virtuelle renvoyée à l'infini.

Dans le deuxième cas, les foyers correspondent, mais il faut auusi que la distance focale de l'onjectif soit supérieure à celle de l'objectif.

Dans le dernier cas, les foyers ne correspondent pas.

Exercice n°14 P 465 : Lunette afocale.

Il faut que le foyer image de l'objectif corresponde avec le foyer objet de l'oculaire, qu isignifie que la distance séparant les deux lentille doit être égale à la somme des deux distances focales : $O_1O_2 \ = \ 100 \ + \ 5 \ = \ 105 \ cm$

2a,b.

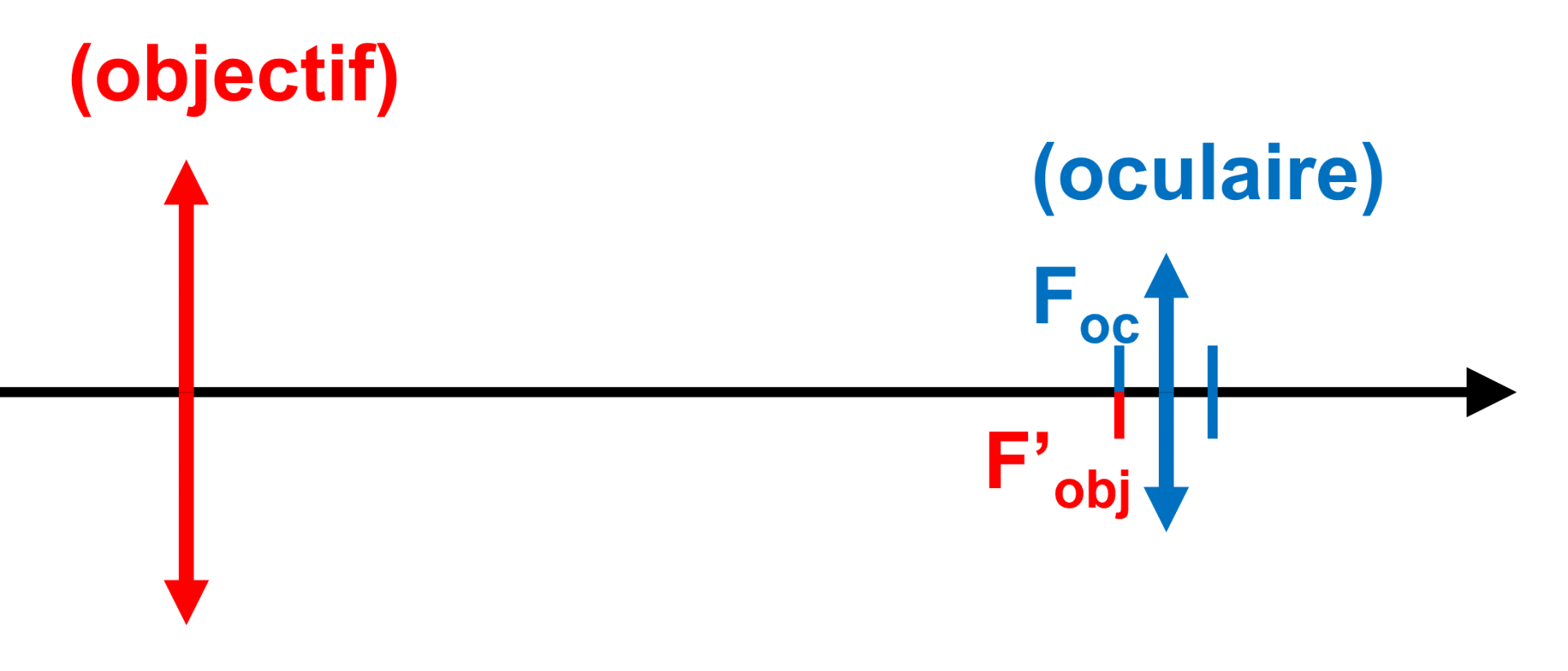
Tale 14 p465

sur votre schéma : La distance entre les deux lentilles est de $\dfrac{105}{10} \ = \ 10,5 \ cm$.

sur votre schéma : La hauteur de l'objectif est : $\dfrac{10}{2} \ = \ 5 \ cm$.

sur votre schéma : La hauteur de l'oculaire est : $\dfrac{6}{2} \ = \ 3 \ cm$.

sur votre schéma : La distance séparant l'objectif des foyers est : $\dfrac{100}{10} \ = \ 10 \ cm$.

Exercice n°16 P 465 : Construction graphique.

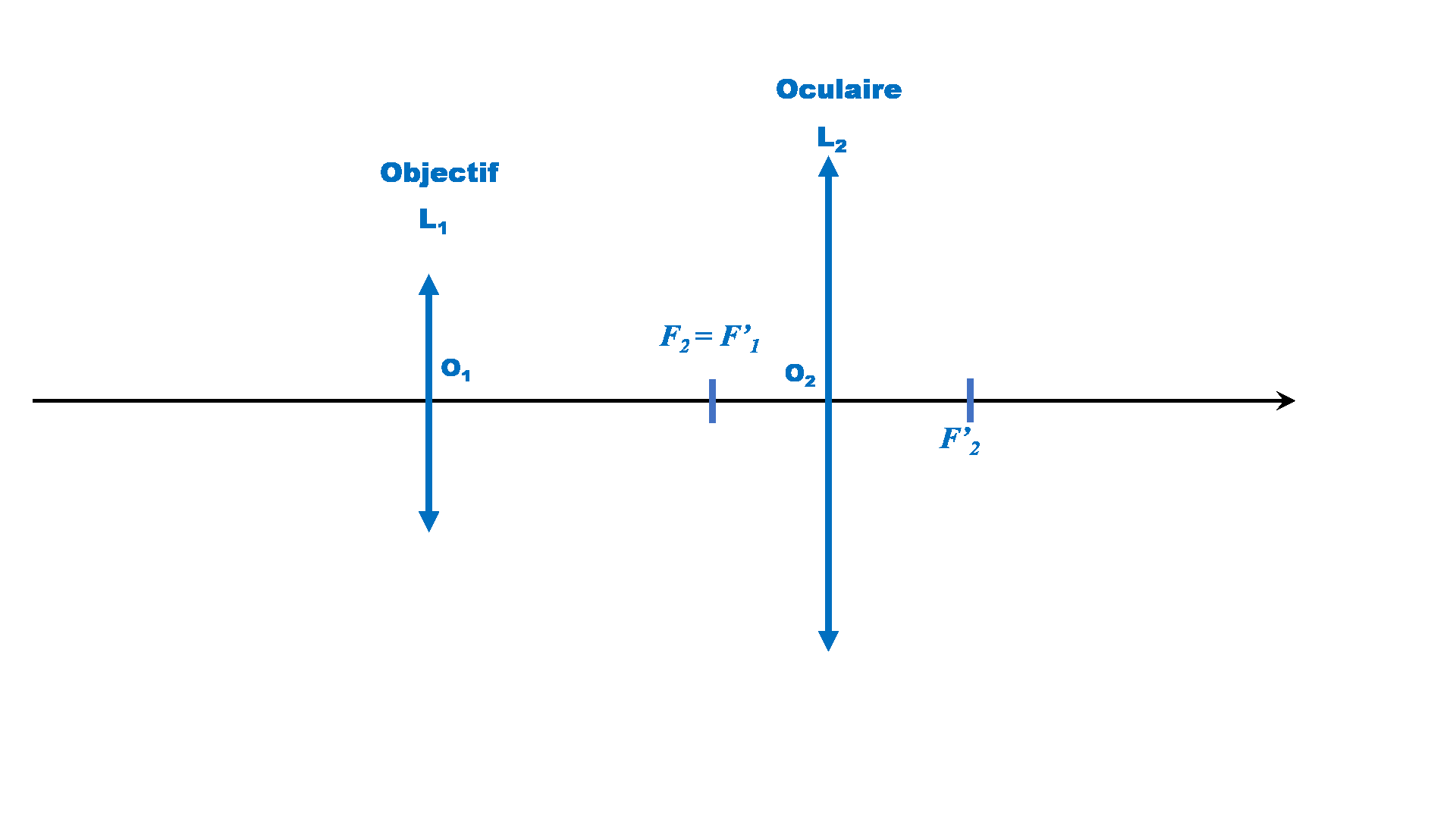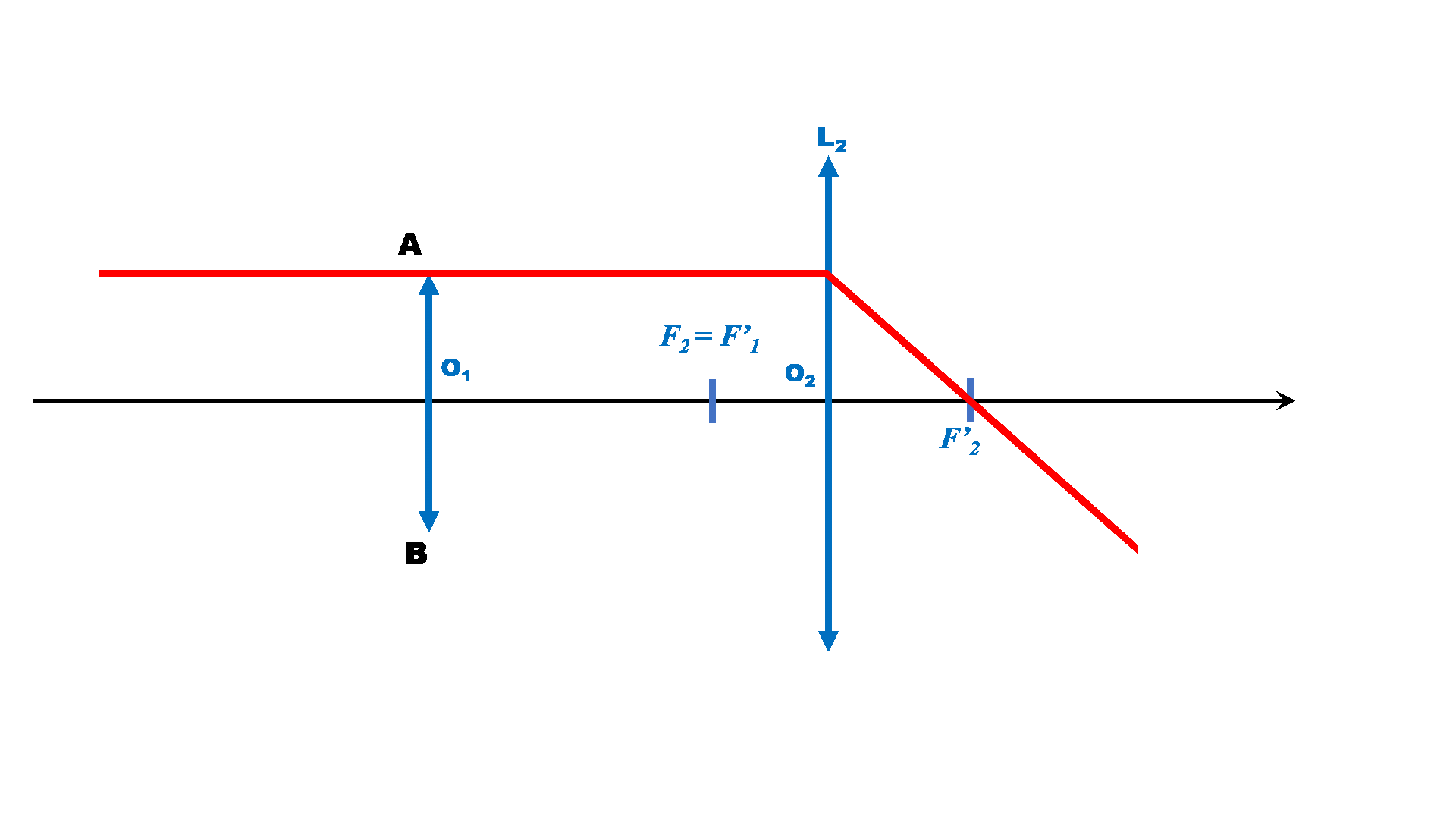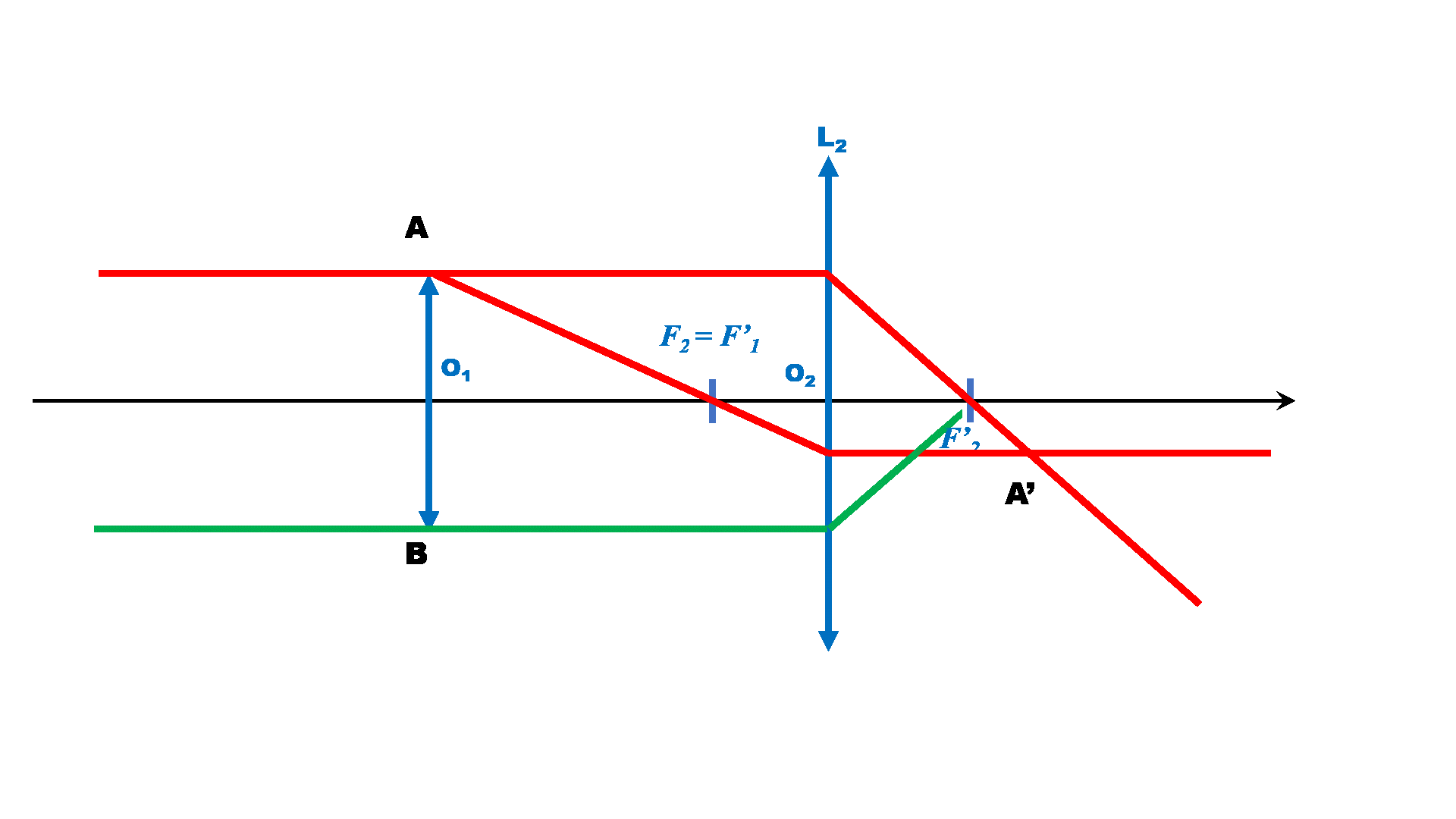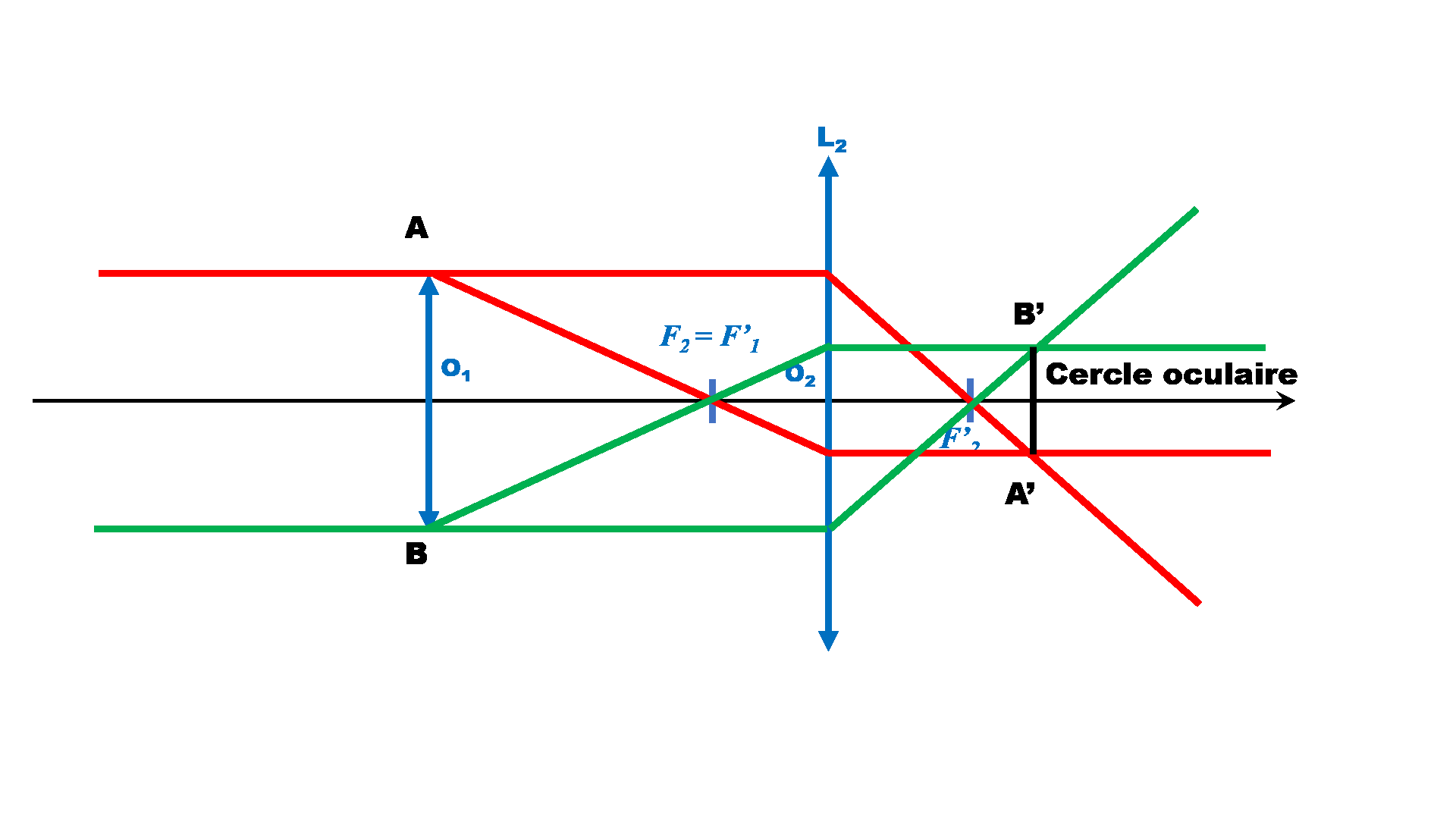
1,2a,3a.

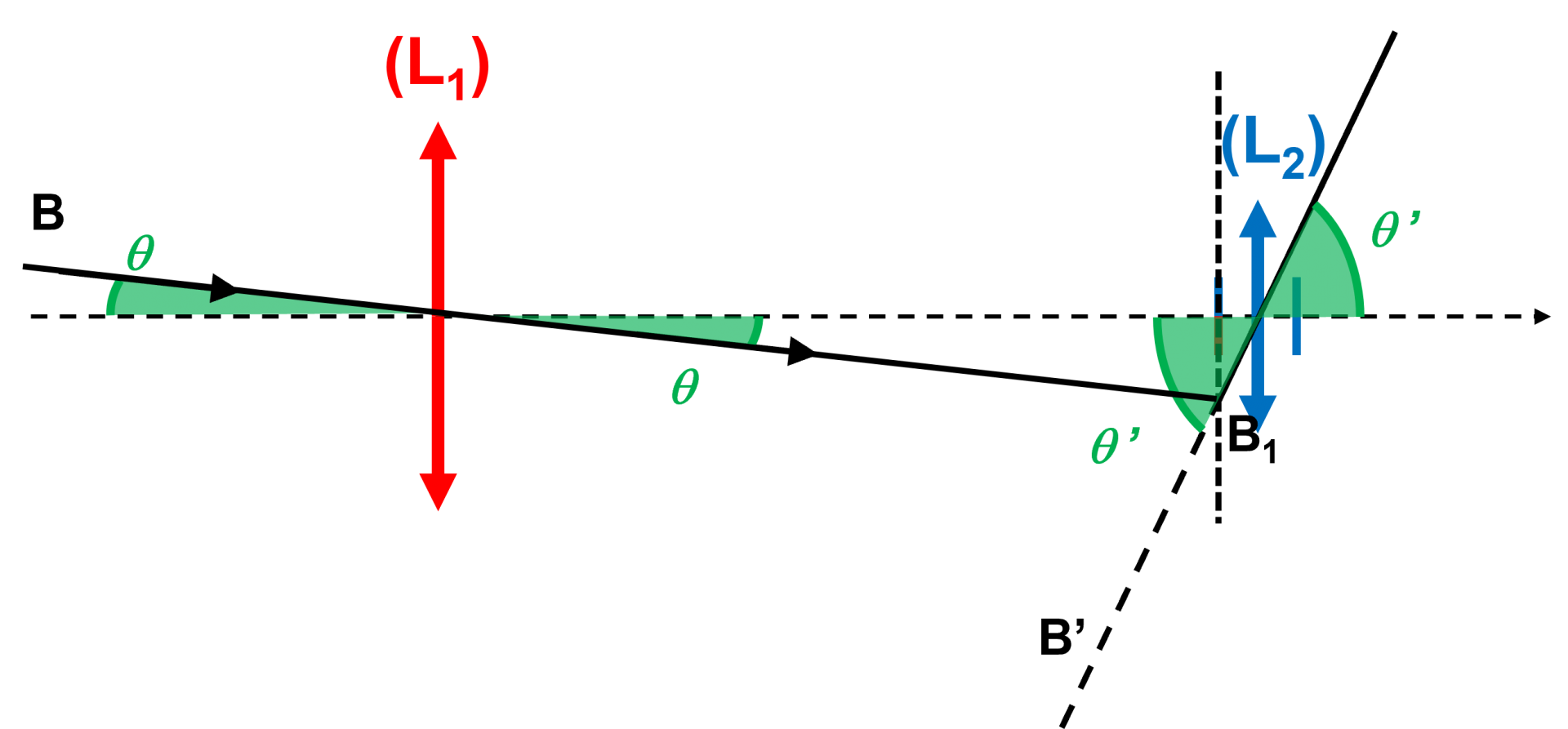
Tale 16 p465

2b.

Le point B observé se trouvant à l'infini, son image $B_1$ se trouve dans le plan focal image de la lentille $L_1$ .

3b.

Le point $B_1$ se trouvant dans le plan focal objet de l'oculaire, l'image finale B' se trouve à l'infini. Un oeil normal n'a pas besoin d'accomoder pour le regarder.

Exercice n°19 P 466 : Grossissement d'une lunette afocale.

Le grossiment d'une lunette afocale est égal au rapport des angles $\theta$ et $\theta \ '$, angles d'entrée du rayon provenant de l'objet observé et angle d'observation de l'image finale : $G \ = \ \dfrac{\theta \ '}{\theta}$

2,3.

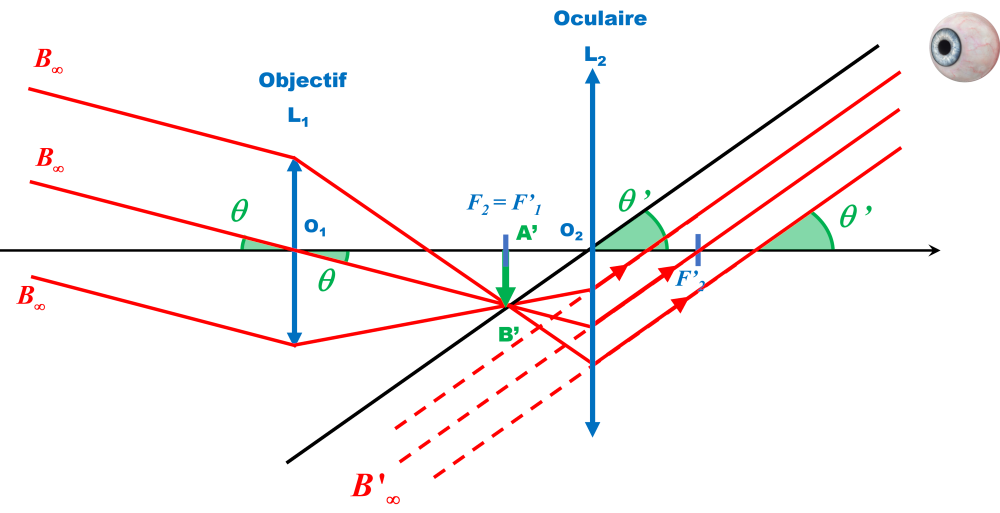
Tale 19 p 466

Dans le triangle $O_1A_1B_1$ rectangle en $A_1$ : $tan(\theta) \ = \ \dfrac{A_1B_1}{O_1A_1}$

L'angle $\theta$ étant très petit : $tan(\theta) \ = \ \theta \ = \ \dfrac{A_1B_1}{f_1} \ '$

De même, dans le triangle $O_1A_1B_1$ rectangle en $A_1$ : $tan(\theta \ ') \ = \ \dfrac{A_1B_1}{O_2A_1}$

L'angle $\theta \ '$ étant très petit : $tan(\theta \ ') \ = \ \theta \ ' \ = \ \dfrac{A_1B_1}{f_2 \ '}$

On a donc : $G \ = \ \dfrac{\theta}{\theta \ '} \ = \ \dfrac{\dfrac{A_1B_1}{f_2 \ '}}{\dfrac{A_1B_1}{f^{ \ '}_1}} \ = \dfrac{A_1B_1}{f_2 \ '} \times \dfrac{f^{ \ '}_1}{A_1B_1} \ = \ \dfrac{f^{ \ '}_1}{f^{ \ '}_2}$

Exercice n°24 P 467 : Message à déchiffrer.

1a,b 2a,2b.

Voir exercice précédent en remplaçant $\theta$ par $\beta$.

$G \ = \ \dfrac{\theta \ '}{\theta } \ = \ \dfrac{f_1}{f_2 } \ = \ \dfrac{300}{50 } \ = \ 6$.

La valeur déterminée précédemment est trop petite pour déchiffrer le message.

Exercice n°29 P 469 : Attention au soleil

1a.

Cercle oculaire :

Cercle oculaire

D'après la relation de conjugaison : $\dfrac{1}{\overline{O_2C}} \ - \ \dfrac{1}{\overline{O_2O_1}} \ = \ \dfrac{1}{f'_2}$

Soit : $\overline{O_2C} \ = \ \dfrac{f_2 \ ' \times \overline{O_2O_1}}{f_2 \ ' \ + \overline{O_2O_1}}$

Soit : $\overline{O_2C} \ = \ \dfrac{12,5 \times (-912,5)}{12,5 + (- 912,5)} \ = \ 12,7 \ mm$

1b.

Le grandissement est : $\gamma \ = \ \dfrac{d}{D} \ = \ \dfrac{O_2C}{O_2O_1}$

Donc : $d \ = \ D \times \dfrac{O_2C}{O_2O_1} \ = \ \dfrac{60 \times 12,7}{912,5} \ = \ 0,84 \ mm$

$r \ = \ \dfrac{\dfrac{P_{oc}}{\pi \times d^{ \ 2} / 4}}{\dfrac{P_{obj}}{\pi \times D^{ \ 2} / 4}} \ = \ \dfrac{D^{ \ 2}}{d^{ \ 2}} \times \ \dfrac{P_{oc}}{P_{obj}}$

Les puissances étant considérées comme les mêmes : $r \ = \ \dfrac{D^{ \ 2}}{d^{ \ 2}}$

Dans notre cas : $r \ = \ \dfrac{D^{ \ 2}}{d^{ \ 2}} \ = \ \dfrac{600^{ \ 2}}{3^{ \ 2}} \ = \ 9,0.10^{ \ 4 }$ !!

La puissance reçue par l'oeil est 90000 fois plusgrande que celle reçue. il y a risque de brûlure et de détérioration irréversible de la rétine en cas d'obervation du Soleil.

Exercice n°30 P 469 : Projection de l'image solaire.

Pour que l'image du cercle oculaire soit plus loin, il faudra reculer l'oculaire.

La nouvelle image doit être située à 30 cm de $O_2$.

Cette image sera celle du foyer $F_1^{ \prime}$ image de l'objectif.

D'après la relation de conjugaison : $\dfrac{1}{\overline{O_2C}} \ - \ \dfrac{1}{\overline{O_2F_1^{ \prime}}} \ = \ \dfrac{1}{f_2}$.

Soit : $\dfrac{1}{\overline{O_2F_1^{ \prime}}} \ = \ \dfrac{1}{\overline{O_2C}} \ - \ \dfrac{1}{f_2}$.

$\Leftrightarrow \ \ \overline{O_2F_1^{ \prime}} \ = \ \dfrac{f_2 \times \overline{O_2C}}{f_2 \ - \ \overline{O_2C}}$

AN : $\Leftrightarrow \ \ \overline{O_2F_1^{ \prime}} \ = \ \dfrac{12,5 \times 300}{12,5 \ - \ 300} \ = \ -13,0 \ mm$

L'oculaire doit être reculé de : $13,0 \ - \ 12,5 \ = \ 0,5 \ mm$

Le grossissement est : $\overline G \ = \ \dfrac{\theta^{ \prime}}{\theta} \ = \ \dfrac{f_1}{f_2} $

Donc : $\theta^{ \prime} \ = \theta \times \dfrac{f_1}{f_2} \ = \ \dfrac{900}{12,5} \times 9,3.10^{ \ -3} \ = \ 0,67 \ rad$

Le diamètre $D_{tache}$ de la tâche vérifie alors : $tan \theta^{ \prime} \ = \ \dfrac{D_{tache}/2}{\overline {O_2C}}$

Donc $D_{tache} \ = \ 2 \times tan \theta \times \overline {O_2C} \ = \ tan \left ( 0,67 \right ) \times 30 \ = \ 47,5 \ cm $

Exercice n°34 P 470 : Cercle oculaire et grossissement

Elle conserve 100% du flux lumineux qui y entre.

2a.

D'après le théorème de Thalès, les lentilles étant parallèles, on peut écrire : $\dfrac{D_{ob}}{a} \ = \ \dfrac{\overline{F_1 ^{ \prime}O_1}}{\overline{F_1 ^{ \prime}O_2}} \ = \ - \ \dfrac{f_1^{ \prime}}{f_2^{ \prime}}$.

Or, le grossissement de la lentille est : $\overline G \ = - \ \dfrac{f_1^{ \prime}}{f_2^{ \prime}}$.

Donc : $\overline G \ = - \ \dfrac{D_{ob}}{a}$.

2b.

Pour que toute la lumière pénètre dans l'oeil, il faudra que le cercle oculaire ait le même diamètre que la pupille.

Soit : $\overline G \ = - \ \dfrac{D_{ob}}{a} \ = \ - \ \dfrac{90}{6} \ = \ -15$.

2c.

$\overline G \ = - \ \dfrac{f_1^{ \prime}}{f_2^{ \prime}} \ \ \ \Leftrightarrow \ \ \ f_2^{ \prime} \ = \ - \dfrac{f_1^{ \prime}}{\overline G} \ = \ \dfrac{60}{15} \ = \ 4,0 \ cm$

Exercice n°37 P 471 : La première photographie d'une étoile.

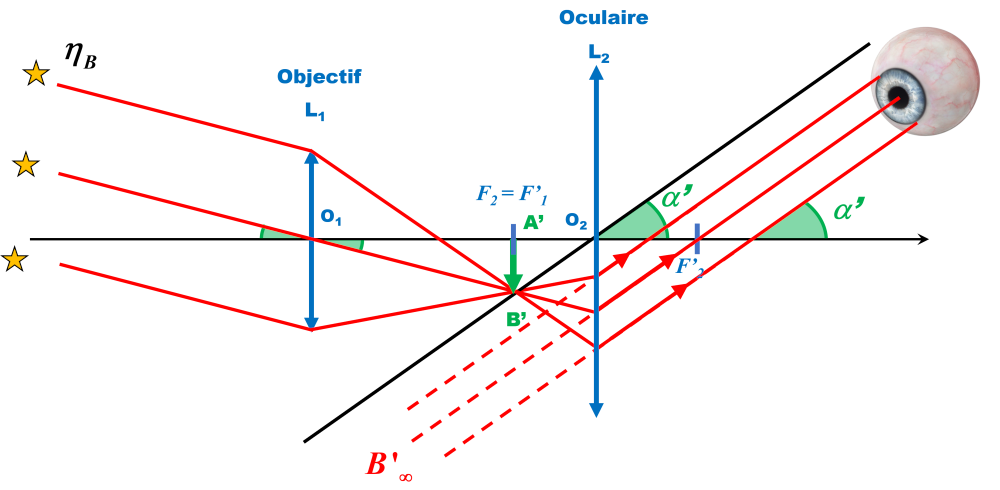
Tale 37 p 471