Mécanique des fluides

Exercice n°10 P 351 : Origine de la poussée d'Archimède.

1a.

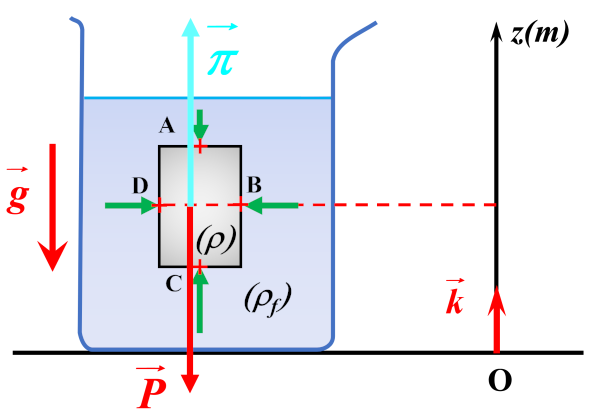
1b.

$\bullet$ Les forces $\overrightarrow {F_C}$ et $\overrightarrow {F_D}$ ont la même direction (l'horizontale), des sens opposés. Elles ont la même norme, s'exerçant aux centres de deux faces ayant la même surface, à la même profondeur : $\overrightarrow {F_C} \ + \ \overrightarrow {F_D} \ = \ \overrightarrow {0}$.

$\bullet$ Les forces $\overrightarrow {F_A}$ et $\overrightarrow {F_A}$ ont la même direction (la verticale), des sens opposés. Par contre, elles n'ont la même norme. C étant plus profond que A, la pression au point C est plus grande que celle s'exerçant en A : $F_C \ > \ F_A$.

2a.

La somme vectorielle de ces forces correspond à la poussée d'Archimède : $\overrightarrow {F_A} \ + \ \overrightarrow {F_B} \ + \ \overrightarrow {F_C} \ + \ \overrightarrow {F_D} \ = \ \overrightarrow \pi$.

2b.

$\overrightarrow \pi \ = \ - \rho _f \times V \times \overrightarrow g \ = \ \ - \rho _f \times V \times g \times \overrightarrow k$.

Exercice n°12 P 351 : Entraînement des spationautes.

1.

$\bullet \ P_1 \ = \ m \times g \ = \ 200 \times 9,81 \ = \ 1,96 \times 10^{3} \ N$

$\bullet \ \pi \ = \ \rho _f \times V \times g \ = \ 1,0.10^{ \ 3} \times 0,19 \times 9,81 \ = \ 1,9 \times 10^{3} \ N$

2.	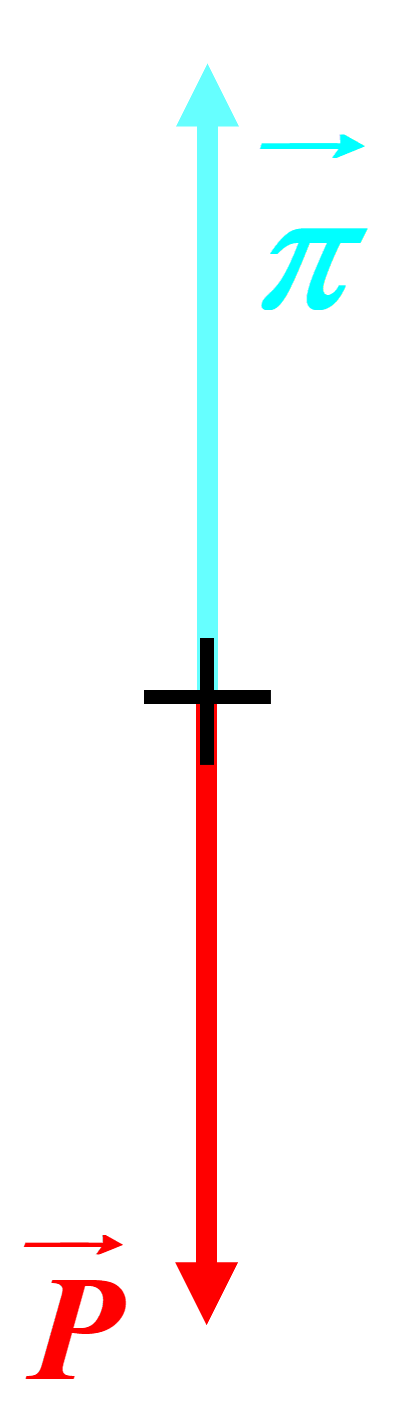3. $P_2 \ = \ P_1 \ - \ \pi \ = \ 1,96 \times 10^{3} \ - \ 1,9 \times 10^{3} \ = \ 9,81 \times 10^{2} N$ La masse correspondante serait : $m \ = \ \dfrac{P_2}{g} \ = \ 10 \ kg$.

Exercice n°13 P 351 : Paramètres d'influence de la poussée d'Archimède.

1.

$\overrightarrow \pi \ = \ - \rho_f \times V \times \overrightarrow g$

$\pi$ : valeur de la poussée d'Archimède, en N.

$\rho_f$ : masse volumique du fluide en $kg.m^{ \ -3}$.

$V$ : volume de fluide déplacé en $m^{ \ 3}$.

$g$ : intensité de la pesanteur en $m.s^{ \ -2}$.

2.

Masse A : $P_A \ = \ 91,8.10^{-3} \times 9,81 \ = \ 9,01.10^{ \ -1} \ N$

Masse A' : $P_{A'} \ = \ 135.10^{-3} \times 9,81 \ = 1,32 \ N$

Masse B : $P_{B} \ = \ 267.10^{-3} \times 9,81 \ = 2,62 \ N$

3a.

Les paramètres mis en jeu sont le corps du solide, la masse du corps, le type de matériau, le type de fluide et la profondeur d'immersion.

3b,c.

$\bullet$ Comparaison des situations 1 et 2.

Le paramètre mis en jeu est le volume du solide (même matériau, même fluide et même profondeur).

$\pi_1 \ = \ 9,01.10^{ \ -1} \ - \ 5,1.10^{ \ -1} \ = \ 0,33 \ N$

$\pi_2 \ = \ 1,32 \ - \ 0,83 \ = \ 0,49 \ N$

Les mesures étant différentes : le volume a une influence sur la poussée d'Archimède.

$\bullet$ Comparaison des situations 1 et 3.

Le paramètre mis en jeu est la profondeur d'immersion (même solide).

Les mesures étant les mêmes : la profondeur n'a pas d'influence.

$\bullet$ Comparaison des situations 1 et 4.

Le paramètre mis en jeu est le type de matériau (même liquide, même profondeur, même volume).

$\pi_1 \ = \ 9,01.10^{ \ -1} \ - \ 5,1.10^{ \ -1} \ = \ 0,33 \ N$

$\pi_4 \ = \ 2,62 \ - \ 2,3 \ = \ 0,32 \ N$

Les mesures étant les mêmes : le type de matériau n'a pas d'influence.

$\bullet$ Comparaison des situations 1 et 5.

Le paramètre mis en jeu est le type de liquide (même solide et même profondeur).

$\pi_1 \ = \ 9,01.10^{ \ -1} \ - \ 5,1.10^{ \ -1} \ = \ 0,33 \ N$

$\pi_5 \ = \ 9,01.10^{ \ -1} \ - \ 0,64 \ = \ 0,26 \ N$

Les mesures étant différentes : le type de fuide a une influence.

Exercice n°14 P 352 : A la station-service.

1a.

Environ 5 minutes... $\Delta t \ = \ 300 \ s$.

1b.

Le débit volumique correspond au volume de fluide qui s'écoule par unité de temps: $D \ = \ \dfrac{V}{\Delta t}$.

AN : $D \ = \ \dfrac{50.10^{ -3}}{300} \ = \ 0,17.10^{ \ -4} \ m^3.s^{ \ -1}$.

1c.

$\dfrac{Q}{D} \ = \ 2,4$. Le temps évalué à la question pécédente, n'est pas correct.

2a.

$S \ = \ \dfrac{\pi \times D^2}{4} \ = \ \dfrac{\pi \times \left ( 16.10^{ \ -3} \right ) ^2}{4} \ = \ 2,0.10^{ \ -4} \ m^2$.

2b.

$Q \ = S \times v \ \Leftrightarrow \ v \ = \ \dfrac{S}{Q} \ = \dfrac{4,0.10^{ \ -4} }{2,0.10^{ \ -4}} \ = \ 2,0 \ m.s^{ \ -1} $

Exercice n°15 P 352 : Circulation sanguine.

1a.

Le débit volumique correspond au volume de fluide qui s'écoule par unité de temps: $D \ = \ \dfrac{V}{\Delta t}$.

1b.

Le débit est de 5,0 L par minute, soit un volume $V \ = \ 5,0.10^{ \ -3} \ m^{ \ 3}$ pendant l'intervalle $\Delta t \ = \ 60 \ $.

AN : $D \ = \ \dfrac{V}{\Delta t} \ = \ \dfrac{5,0.10^{ \ -3}}{60} \ = \ 8,3.10^{ \ -5} \ m^3.s^{ \ -1}$.

2a.

D'après la réponse précédente, chaque seconde, $8,3.10^{ \ -5} \ m^3$ de sang s'écoule.

2b.

$D \ = \ \dfrac{V}{\Delta t} \ = \ \dfrac{S \times \Delta L}{\Delta t} \ = \ S \times v$, donc : $v \ = \ \dfrac{D}{S} \ = \ \dfrac{8,3.10^{ \ -5}}{2,5.10^{ \ -4}} \ = \ 0,33 \ m.s^{ \ -1}$

3a.

Le débit sanguin est conservé : $D \ = \ 8,3.10^{ \ -5} \ m^3.s^{ \ -1}$

3b.

D'après la définition, $D \ = \ S \times v$. Donc, à $D$ constant, si $S$ diminue, $v$ augmente.

Exercice n°18 P 352 : Ecoulement dans une bouteille percée.

1a.

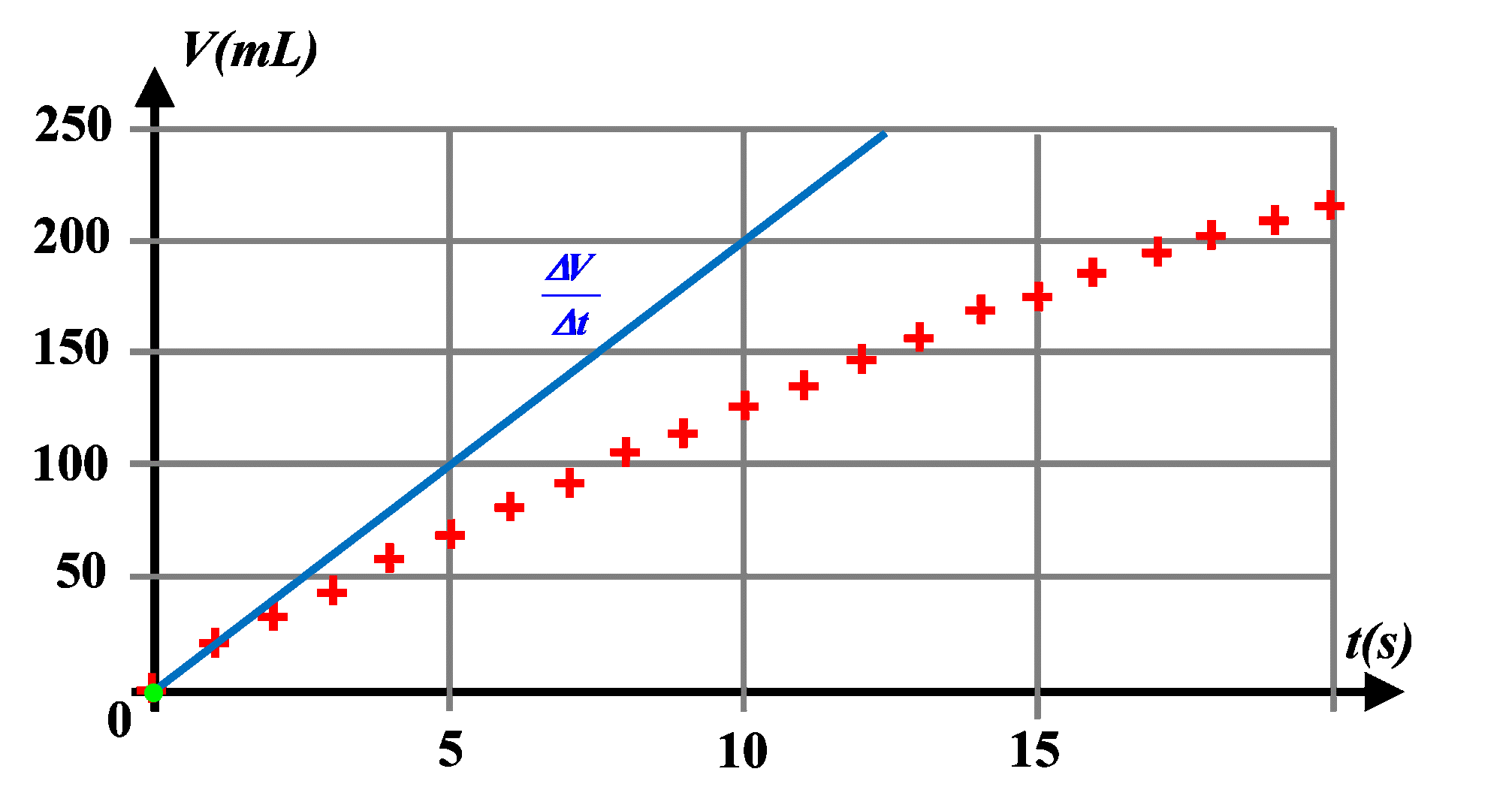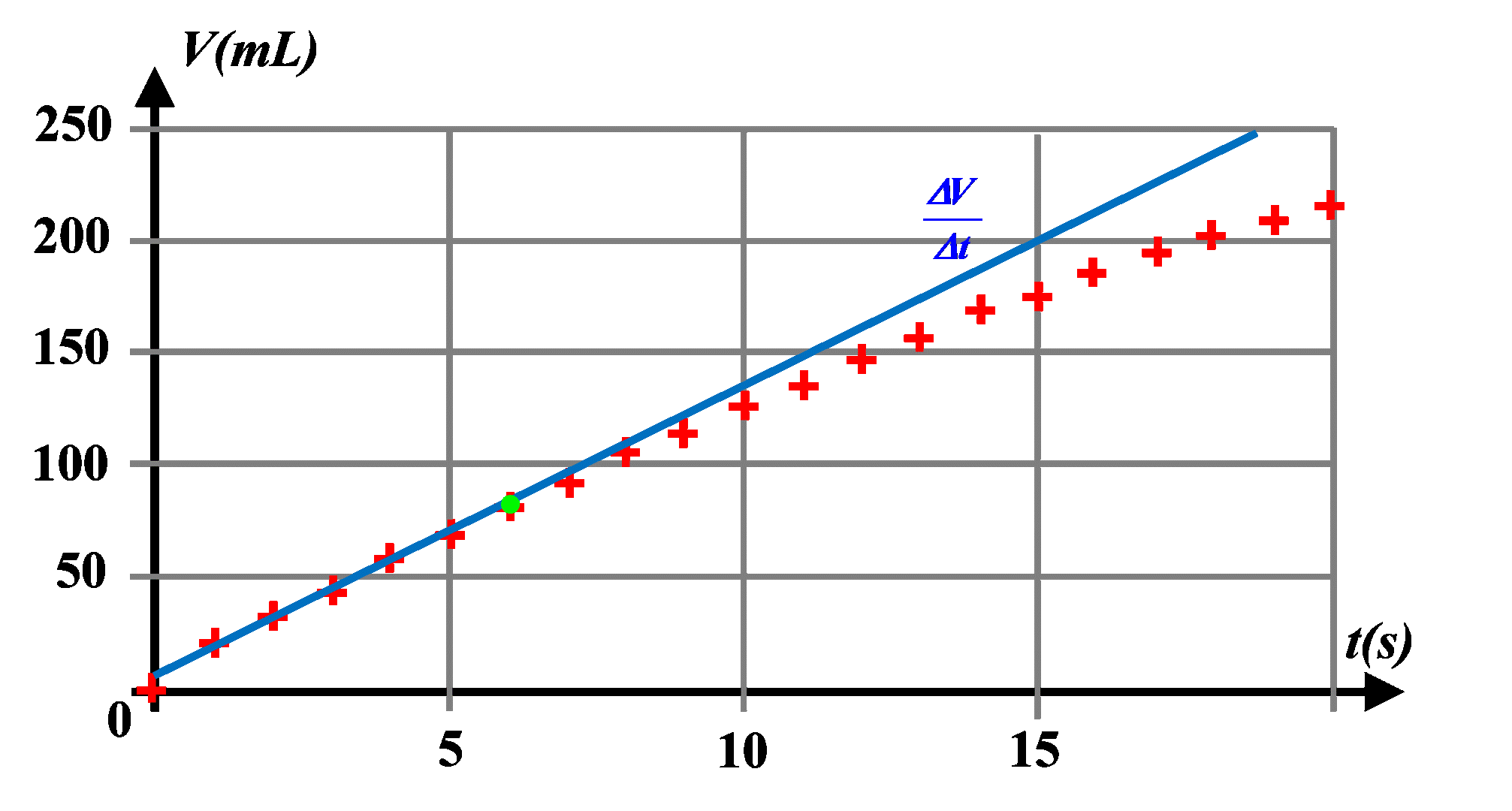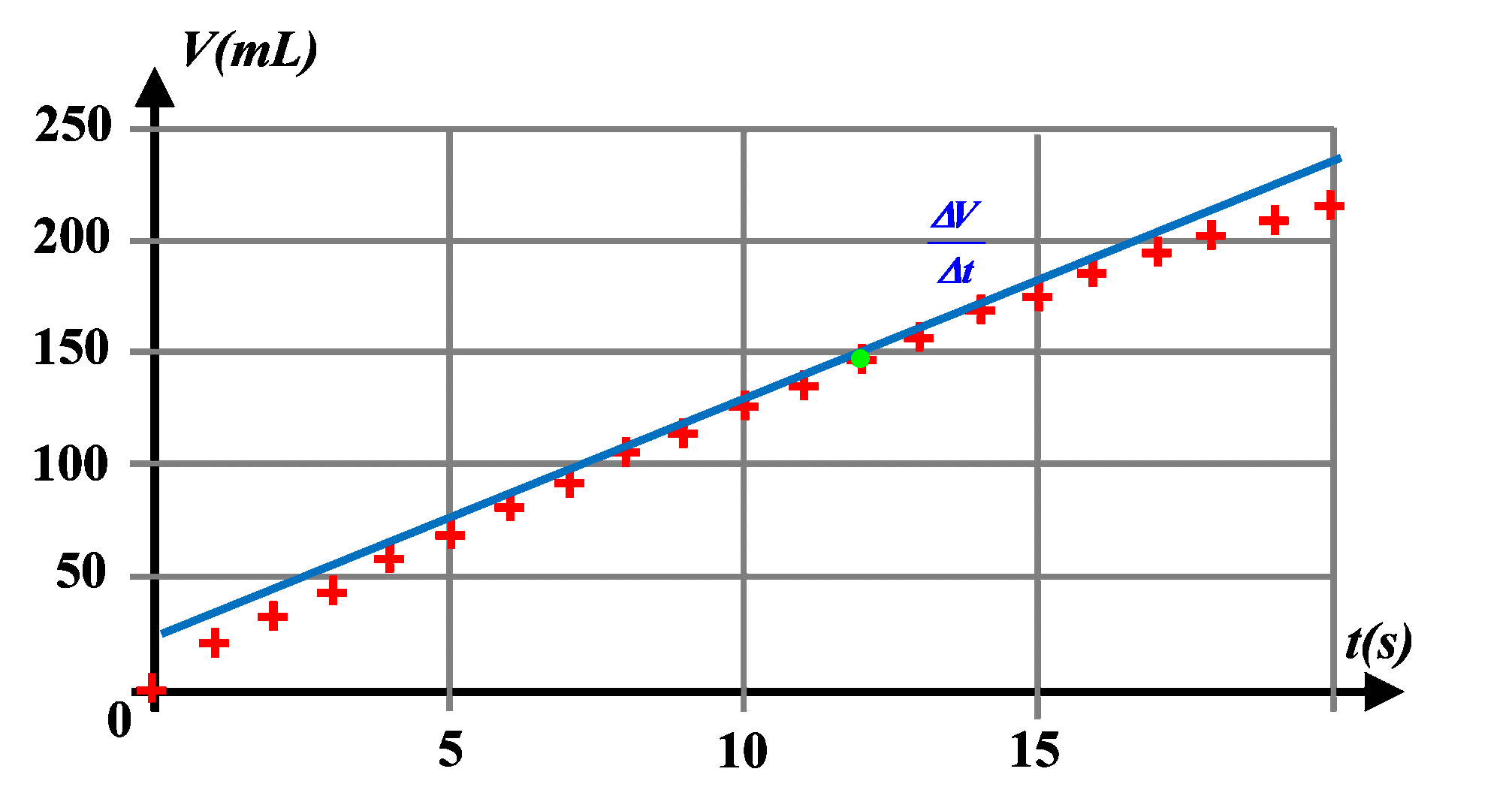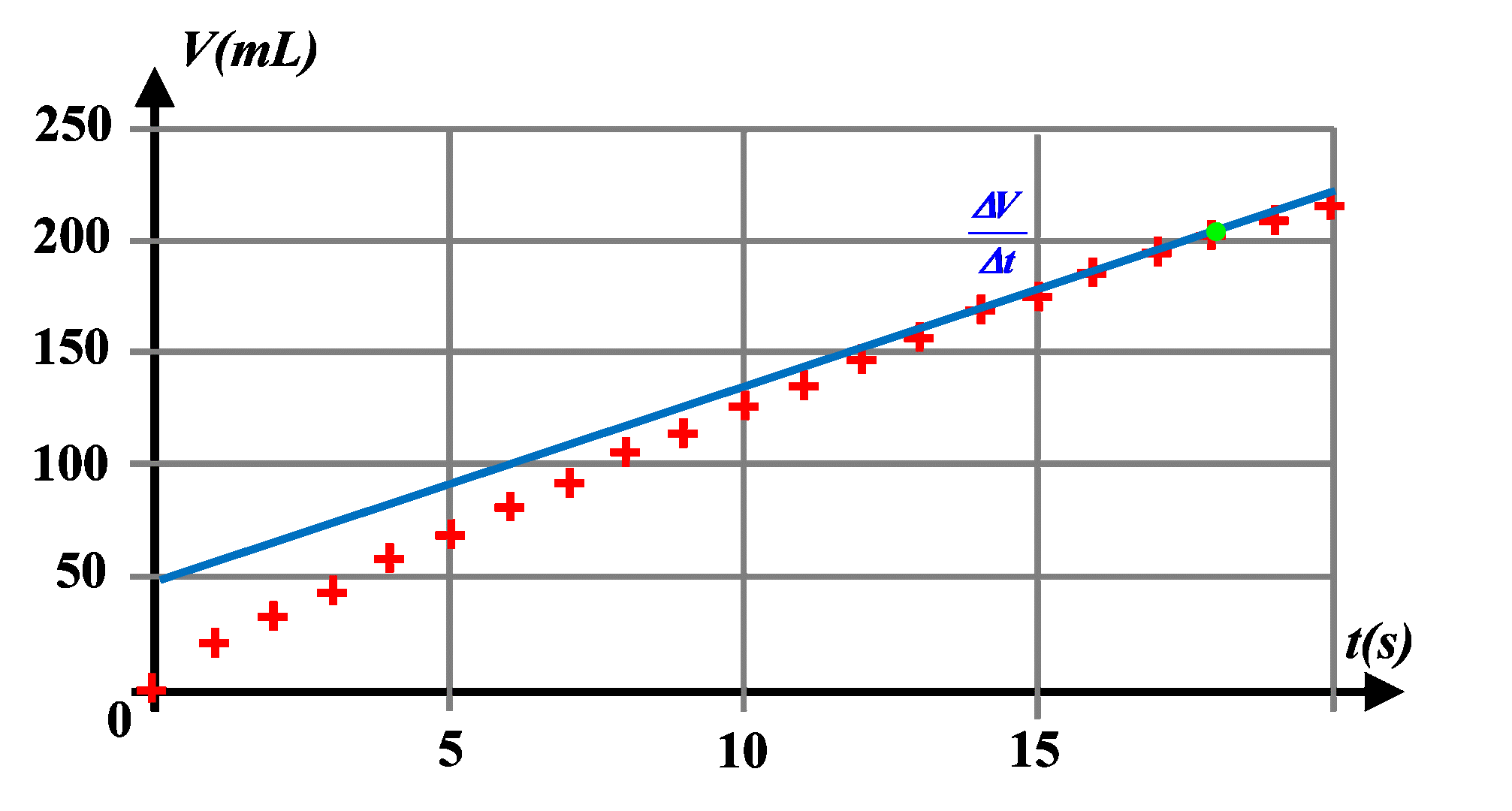
D'après le graphique, $V(t)$ n'est pas une fonction linéaire. Les coefficients directeur des tangentes à la courbe $V(t)$ correspondant au débit $D \ = \ \dfrac{\Delta V}{\Delta t}$ diminuent avec le temps.

1b.

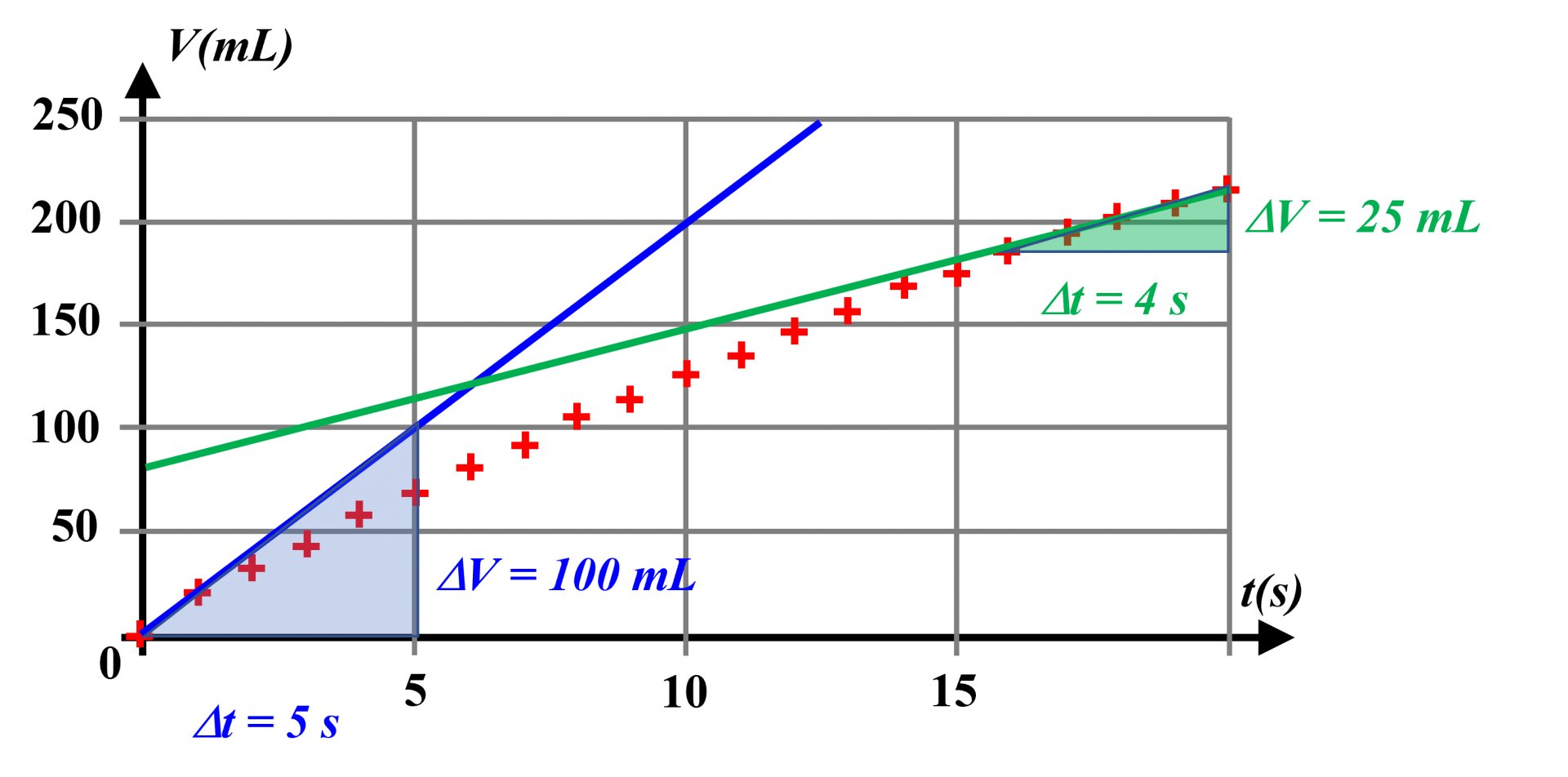
A l'instant $t \ = \ 0 \ s$ : $D_0 \ = \ \dfrac{100}{5} \ = \ 20 \ mL.s^{ \ -1}$

A l'instant $t \ = \ 16 \ s$ : $D_{16} \ = \ \dfrac{25}{4} \ = \ 6,3 \ mL.s^{ \ -1}$

Le débit volumique n'est pas constant.

Exercice n°19 P 353 : Ecoulement sans frottement.

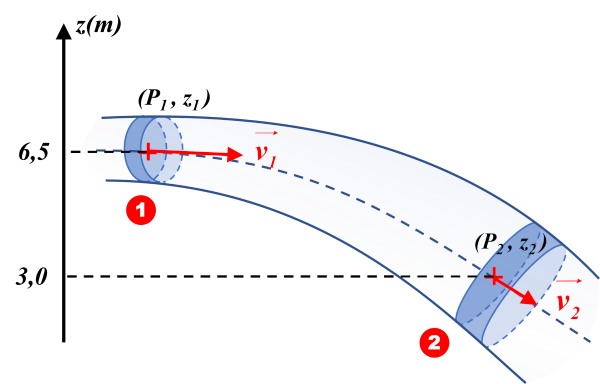
1.

$\dfrac{ \rho \times v_1^2}{2} \ + \ \rho \times g \times z_1 \ + \ p_1 \ = \ \dfrac{ \rho \times v_2^2}{2} \ + \ \rho \times g \times z_2 \ + \ p_2$

$\dfrac{ 1000 \times 1,0^2}{2} \ + \ 1000 \times g \times 6,5 \ + \ 1,0.10^{ \ 5} \ = \ \dfrac{ 1000 \times 0,45^2}{2} \ + \ 1000 \times g \times 3,0 \ + \ p_2$

$1,64.10^{ \ 5} \ = \ 2,95.10^{ \ 4} \ + \ p_2$

2.

$p_2 \ = \dfrac{ \rho \times v_1^2}{2} \ + \ \rho \times g \times z_1 \ + \ p_1 \ - \ \dfrac{ \rho \times v_2^2}{2} \ + \ \rho \times g \times z_2 $

$p_2 \ = \dfrac{ \rho \times \left ( v_1^2 \ - \ v_1^2 \right ) }{2} \ + \ \rho \times g \times \left ( z_1 \ - \ z_2 \right ) \ + \ p_1 $

$p_2 \ = \ 1,64.10^{ \ 5} \ - \ 2,95.10^{ \ 4} \ = \ 1,35.10^{ \ 5} \ Pa$

Exercice n°20 P 353 : Analyse dimensionnelle.

Relation de Bernoulli : $\dfrac{ \rho \times v^2}{2} \ + \ \rho \times g \times z \ + \ p \ = \ Cste$

1.

$\rho$ : masse volumique du fluide en $kg.m^{ \ -3}$

$v$ : vitesse du fluide au ppint considéré en $m.s^{ \ -1}$.

$g$ : accélération de la pesanteur en $m.s^{ \ -2}$.

$p_1$ : pression au point du fluide en $Pa$.

2.

$\left [ \dfrac{ \rho \times v^2}{2} \right ] \ = \ kg.m^{ \ -3} \times \left (m.s^{ \ -1} \right ) ^2 \ = kg.m^{ \ -3}.m^2.s^{ \ -2} \ = \ kg.m^{ \ -1}.s^{ \ -2}$

$\left [ \rho \times \ g \times z \right ] \ = \ kg.m^{ \ -3} \times m.s^{ \ -2} \times m = kg.m^{ \ -3}.m^{ \ 2}.s^{ \ -1} \ = \ kg.m^{ \ -1}.s^{ \ -2}$

La pression est le rapport d'une force à une surface : $\left [ p \right ] \ = \ N.m^{ \ -2}$

D'après la 2ème loi de Newton $\left ( \Sigma \overrightarrow F \ = \ m \times \overrightarrow a \right )$, la force est le produit d'une masse à une accélération : $\left [ p \right ] \ = \ kg.m.s^{ \ -2}.m^{ \ -2} = \ kg.m^{ \ -1}.s^{ \ -2}$

Les trois termes de la relation de Bernoulli ont bien la même dimension.

Exercice n°21 P 353 : Chimie industrielle de synthèse.

Le débit est constant : $D_A \ = \ D_B \ \Leftrightarrow S_A \times v_A \ = \ S_B \times v_B$.

La canalisation ayant de même rayon, la surface en A et en B est la même, donc : $v_A \ = \ v_B$.

D'après la relation de Bernoulli : $\dfrac{ \rho \times v_A^2}{2} \ + \ \rho \times g \times z_A \ + \ p_A \ = \ \dfrac{ \rho \times v_B^2}{2} \ + \ \rho \times g \times z_B \ + \ p_B$

$\Leftrightarrow \rho \times g \times z_A \ + \ p_A \ = \ \rho \times g \times z_B \ + \ p_B $.

$\Leftrightarrow p_B \ = \rho \times g \times \left ( z_A \ - \ z_B \right ) \ + \ p_A $.

AN : $p_B \ = 784 \times 9,81 \times \left ( 0,5 \ - \ 4,5 \right ) \ + \ 3,5 \times 1,13.10^{ \ 5} \ = \ 3,24.10^{ \ 5} \ Pa$.

Exercice n°22 P 353 : Rétrécissement d'un écoulement.

1.

A débit constant, $D_A \ = \ D_B \ \Leftrightarrow S_A \times v_A \ = \ S_B \times v_B \ \Leftrightarrow \ \dfrac{S_A}{S_B} \ = \dfrac{v_B}{v_A}$.

Comme $S_A > S_B$ : $v_B < v_A$

2a.

Relation de Bernoulli : $\dfrac{ \rho \times v_A^2}{2} \ + \ \rho \times g \times z_A \ + \ p_A \ = \ \dfrac{ \rho \times v_B^2}{2} \ + \ \rho \times g \times z_B \ + \ p_B $

A et B étant à la même altitude, $z_A \ = \ z_B$ on a : $\dfrac{ \rho \times v_A^2}{2} \ + \ p_A \ = \ \dfrac{ \rho \times v_B^2}{2} \ + \ p_B $

2b.

$ \dfrac{ \rho \times v_B^2}{2} \ - \ \dfrac{ \rho \times v_A^2}{2} \ = p_A \ - \ p_B $

$ \Leftrightarrow \ \dfrac{\rho}{2} \times \left ( v_B^2 \ - \ v_A^2 \right ) \ = p_A \ - \ p_B $

$ \Leftrightarrow \ v_B^2 \ - \ v_A^2 \ = \left ( p_A \ - \ p_B \right ) \times \dfrac{2}{\rho} $

$ \Leftrightarrow \ v_B^2 \ = \ \dfrac {2 \left ( p_A \ - \ p_B \right )}{\rho} \ + \ v_A^2 $

$ \Leftrightarrow \ v_B \ = \ \sqrt{\dfrac {2 \left (p_A \ - \ p_B \right )}{\rho} \ + \ v_A^2} $

AN : $v_B \ = \ \sqrt{\dfrac {2 \left (1002.10^{ \ 2} \ - \ 987 \times 10^{ \ 2} \right )}{825} \ + \ 4,5^2} \ = \ 4,9 \ m.s^{ \ -1}$

On obtient bien au point B une vitesse supérieure à celle au point A.

Exercice n°23 P 353 : La portance.

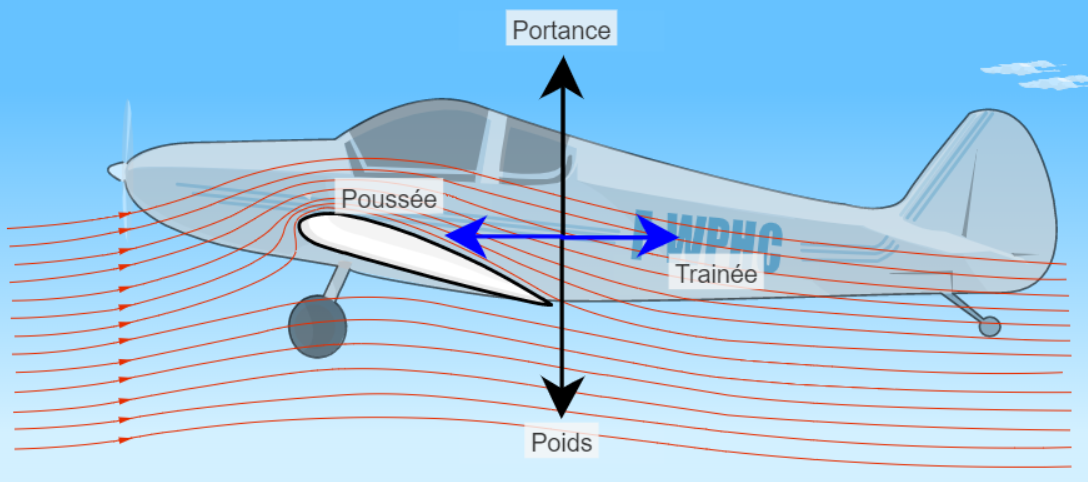
L'air parcourt une distance plus grande sur la surface supérieure de l'aile pendant le même intervalle de temps que celui sur la surface inférieure.

La vitesse de l'air sur la face supérieure est donc plus grande que la vitesse de l'air sur la face inférieure.

La vitesse de l'air sur la face supérieure est donc plus grande que la vitesse de l'air sur la face inférieure.

La relation de Bernoulli : $\dfrac{ \rho \times v_{sup}^2}{2} \ + \ \rho \times g \times z_{sup} \ + \ p_{sup} \ = \ \dfrac{ \rho \times v_{inf}^2}{2} \ + \ \rho \times g \times z_{inf} \ + \ p_{inf} $

A la même altitude : $\dfrac{ \rho \times v_{sup}^2}{2} \ + \ p_{sup} \ = \ \dfrac{ \rho \times v_{inf}^2}{2} \ + \ p_{inf} $

$\Leftrightarrow \ p_{inf} \ - \ p_{sup} \ = \ \dfrac{\rho}{2} \times \left ( v_{sup}^2 \ - \ v_{inf}^2 \right ) \ > \ 0$

La pression sur la face inférieure est donc supérieure à la pression sur la face inférieure. Cette différence de pression induit une force verticale, orientée vers le haut : la portance.

Exercice n°27 P 355 : Le ludion.

1a,b.

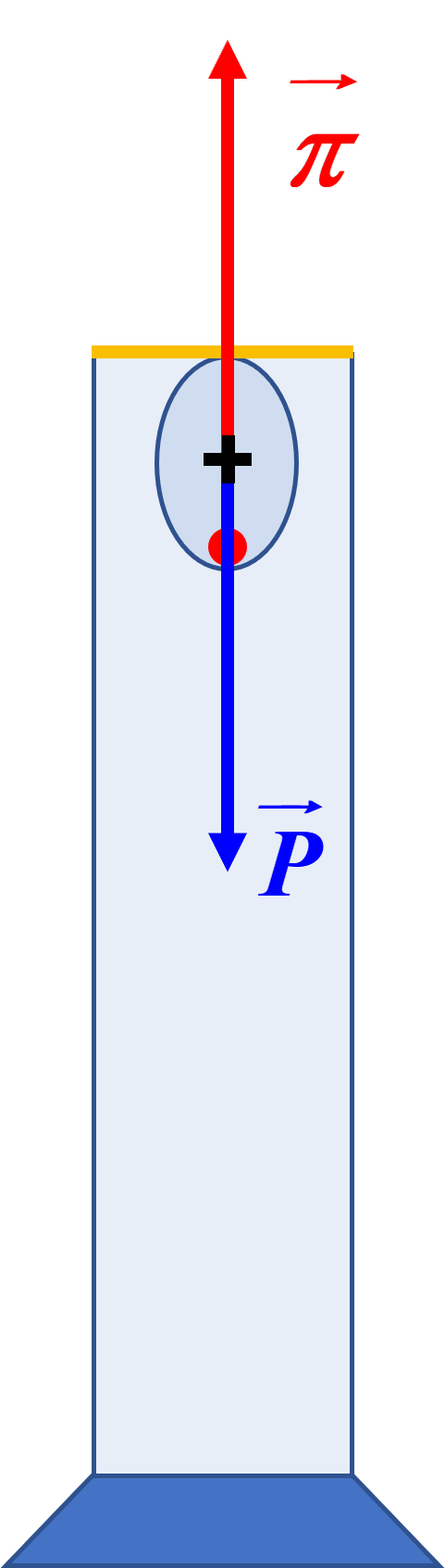A l'équilibre, le poids $\overrightarrow P$ et la poussée d'Archimède $\overrightarrow \pi$ se compensent : $m_L \times g \ = \ \rho_{eau} \times \left ( V_A \ + \ v_B \right ) \times g $ $V_A \ = \ \dfrac{m_L}{\rho_{eau}} \ - \ v_B$ $AN : V_A \ = \ \dfrac{6,8.10^{ \ -3}}{\rho_{1000}} \ - \ 1,8.10^{ \ -6} \ = \ 5,0.10^{ \ -6} \ m^{\ 3}$ soit $5 \ cm^{ \ 3}$

2a.

En comprimant la membrane, le volume $V_A$ diminue.

2b.

La quantité de matière en air n'ayant pas changé, la masse totale du ludion est la même.

Alors, la valeur de la poussée d'Archimède ne compense plus le poids. Le ludion descend.

Exercice n°29 P 356 : Fontaine à eau.

1a.

Le dédit est : $D \ = \ S \times v \ \Leftrightarrow \ v \ = \ \dfrac{D}{S} \ = \ \dfrac {D}{\pi d^2/4} \ = \ \dfrac{4 \times D}{\pi d^2} \ = \ \dfrac{4 \times 1/60}{\pi \left ( 25.10^{ \ -3} \right ) ^2} \ = \ 34 m.s^{ \ -1}$

La conservation du débit s'écrit : $D \ = \ S_1 \times v_1 \ = \ S_2 \times v_2 \ \Leftrightarrow \dfrac{S_1}{S_2} \ = \ \dfrac{v_2}{v_1}$

Ainsi, si $S_2 < S_1$, le rapport $\dfrac{S_1}{S_2} \ = \ \dfrac{v_1}{v_2}$ est inférieur à 1. Et donc $\dfrac{v_1}{v_2} < 1$.

La surface à l'orifice étant supérieure à celle à l'entrée de la tuyère, la vitesse est plus grande que la vitesse à l'entrée de la tuyère est supérieure à celle dans la canalisation.