Méthodes Chimiques

13 P 75 : Acide sulfurique concentré.

1. w = 95% correspond au titre massique. C'est la masse d'un volume d'acide sulfurique $H_2SO_4$ dans un même volume de solution : $ w = \dfrac {m_{soluté}}{m_{solution}} \times 100 $.

2. La solution du laboratoire est : $\dfrac {95}{51} = 1,9 $ fois plus concentrée.

3. $c = \dfrac {\rho_{eau} \times d \times w}{M} $ donc : $ d = \dfrac {c \times M}{\rho_{eau} \times w} = \dfrac {17,8 \times 98}{1 \times 0,95 } =1,84  $.

14 P 75 : Ammoniac.

1. Une  solution d'ammoniaque $NH_4OH$ peut être préparé en dissolvant de l'ammoniac $NH_3$ gazeux dans de l'eau.

2.  $ c = \dfrac {\rho _{eau} \times d \times w}{M} = \dfrac {1000 \times 0,95 \times 0,2}{17} = 11,2 \ g.mol^{ \ -1} $.

16 P 75 : Qu'est-ce qu'un titrage.

1. 

2.  Dans l'erlenmeyer, la concentration en solution titrante reste nulle jusquà l'équivalence, puis augmente. La quantité de matière en solution titrée diminue jusqu'à léquivalence puis devient nulle.

3.  A l'équivalence, les quantités de matière en espèce titrée et titrante sont dans les conditions stoechimoétriques.

18 P 76 : Titrage d'un acide ou d'une base ?

1. 

2.

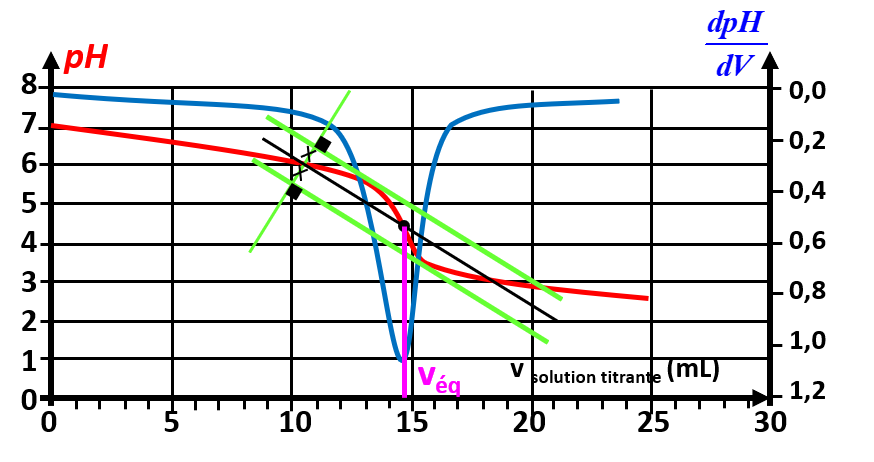
L'équivalence peut  être repérée par la méthode des tangentes.

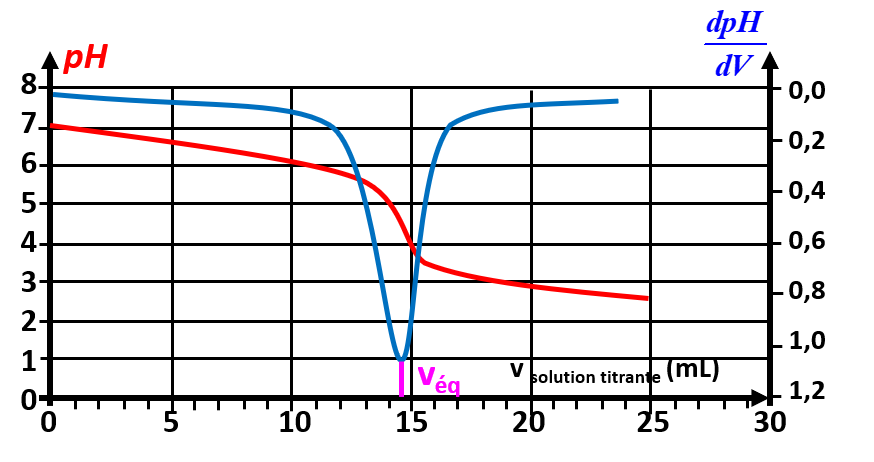
L'équivalence peut  être repérée au maximum de la dérivée du pH : $\dfrac {dpH}{dv}$.

3. Les valeurs du pH diminuent, la concentration en ions hydronium augmente : on dose une solution basique par une solution acide.

RQ : la valeur initiale du pH est de 7. La solution est neutre au départ.

4. On aurait pu répérer l'équivalence à l'aide d'un indicateur coloré approprié, ou en mesurant la conductivité de la solution (conductimètre à la place du pH-mètre).

19 P 76 : Vitamine C 500.

1. $C_6H_8O_{6(aq)} + HO_{(aq)}^{ \ - } \overleftarrow{\longrightarrow} C_6H_8O_{6(aq)}^{ \ -} + H_2O_{(l)}$

2. 

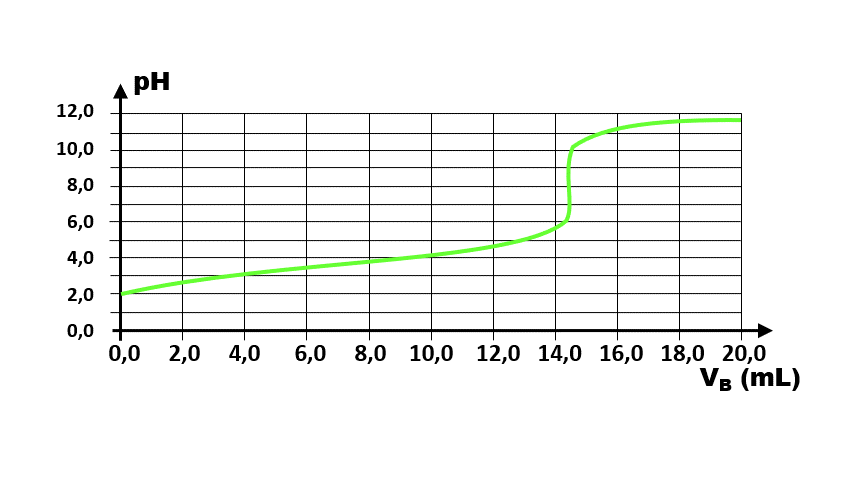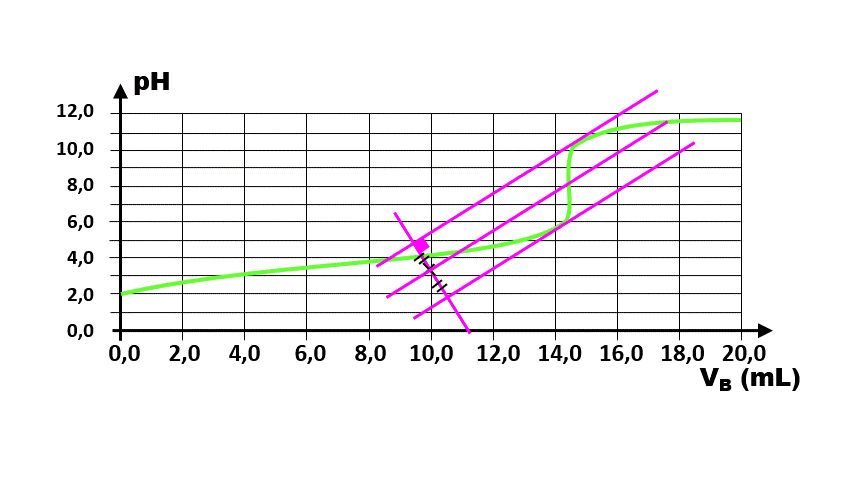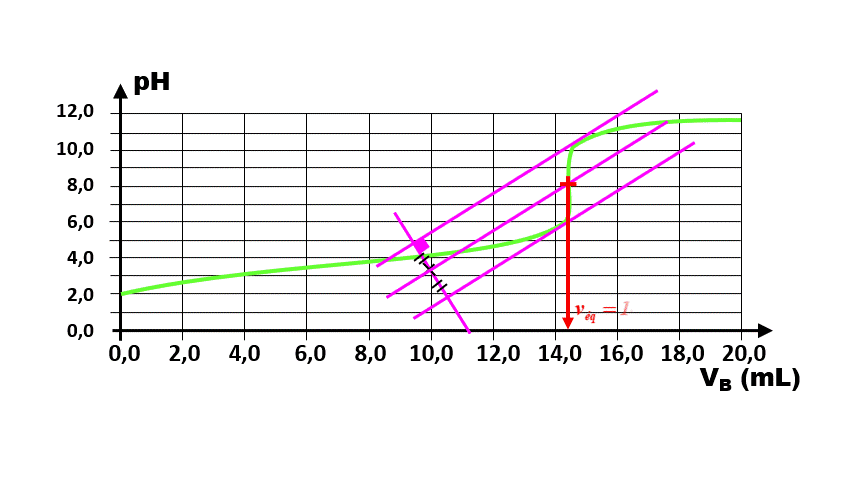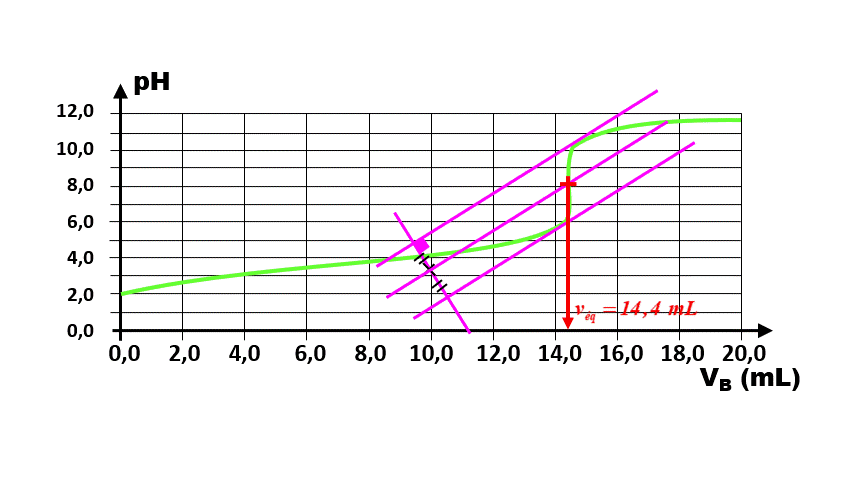3. A l'équivalence, les espèces dosées et dosantes sont dans les conditions stoechiométriques. Ici, $n_{OH^{-}} = n_{C_6H_8O_{6(aq)}} = 2,00.10^{ \ -2 } \times 14,4.10^{ \ -3} =  2,88.10^{ \ -4} \ mol$ dans les 10 mL dosés.

4. La masse correspondante, est donc : $m_{10 \ mL} =2,88.10^{ \ -4} \times 176 = 5,07.10^{-2} \ g$. Soit une masse $m_{100 \ mL} = 10 \times  5,07.10^{-1} \ g = 507 \ mg $. D'où le nom de vitamine C "500".

20 P 76 : Volume équivalent.

1. La série de mesures est de type A : on a effectué la mesure dans les mêmes conditions expérimentales pour obtenir 16 valeurs. On effectuera une moyenne, déterminera un écart-type, puis une incertitude-type.

2. Les valeurs sont différentes car une mesure ne peut pas conduire à une valeur rigoureuse, mais à des valeurs approchées.

3. Un graphique donne les effectifs des mesures :

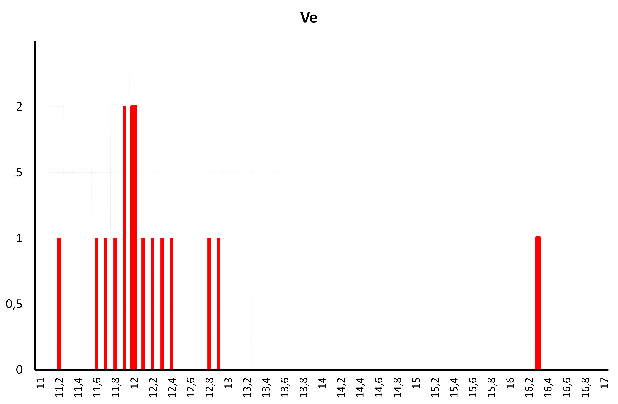
Les valeurs sont regroupées autour de la valeur $V_E=12 \ mL$. On supprimera les valeurs 11,2 ; 12,8 ; 12,9 et 16,3.

4a. On effectue une moyenne à l'aide des 12 valeurs conservées : $\overline {V_E}=12,0 \ mL$

4b. L'écart-type obtenu a pour valeur : $\sigma = 0,26299.... \ mL$ et l'incertitude-type : $u \left  ( V_E \right )= \dfrac {\sigma}{12}=0,02 \ mL$

4c.  $\overline {V_E}=12,0 \pm 0,02 \ mL$

22 P 77 : Titrage de l'aspirine.

1. Réaction : $AH_{(aq)} \ + \  HO^{ \ - }_{(aq)} \longrightarrow \ A^{ \ -}_{(aq)} \ + \ H_2O_{(l)} $

2. Avant l'équivalence, on ajoute des ions $HO^{ \ - }_{(aq)}$ et des ions $Na^{ \ + }_{(aq)}$, il se forme des ions $A^{ \ - }_{(aq)}$, la conductance augmente.

Après l'équivalence, tout l'acide $AH_{(aq)}$ a été consommé, on continue à ajouter des ions $HO^{ \ - }_{(aq)}$ et des ions $Na^{ \ + }_{(aq)}$, la conductance augmente d'avantage.

3. 

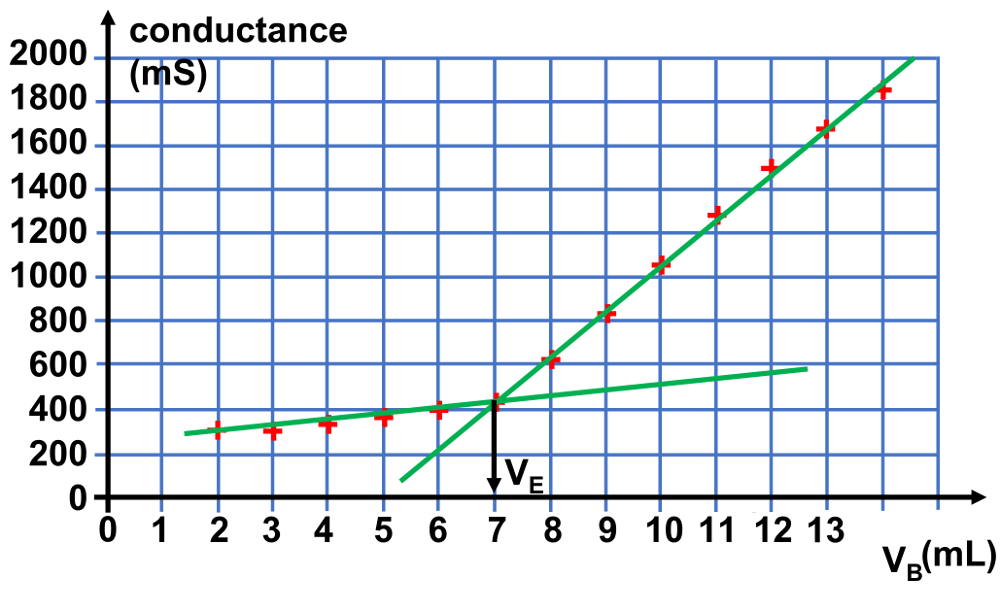
Le volume équivalent est : $V_E \ = \ 7 \ mL $

4a. A l'équivalence, les réactifs sont dans les conditions stoechiométriques. Ici, $n_{AH} \ = \ n_{HO^{ \ -}$

Soit : $c_A \ = \  \dfrac{c_B \times V_E}{V_A} \ = \  \dfrac{1,0.10^{ \ -1 \times 7}}{100} \ = \ 7,0.10^{ \ -3} \ mol.L^{ \ -1}$

4b. La quantité de matière dans la solution initiale est donc : $n_{AH} \ = \ c_A \times V \ = \ 7,0.10^{ \ -3} \times 250.10^{ \ -3} \ = \ 1,75.10^{ \ -3 } \ mol$, on en déduit une masse $m \ = 1,75.10^{ \ -3 } \times 180 \ = 0,32 \ g$. Ce qui correspond à la valeur attendue.

23 P 77 : Titrage des ions chlorure.

 $Ag_{(aq)}^{ \ +} \ + \  Cl^{ \ - }_{(aq)} \longrightarrow \ AgCl_{(s)}  $

1. Montage : voir celui de l'exercice 18, en remplaçant le pH-mètre par un conductimètre.

La solution titrante est la solution de nitrate d'argent, la solution titrée est le lait dilué.

2. 

Au départ du titrage, les ions argent disparaissent. La conductivité est due aux ions nitrate $NO_3^{ \ -}$ versés qui ne réagissent pas. La concentration en ions chlorure $Cl^{ \ -}$ diminue. La conductivité des ions nitrate étant inférieure à celle des ions chlorure, la conductivité globale diminue.

Après l'équivalence, la totalité des ions chlorure a disparu. On continue à ajouter des ions argent et des ions nitrate, la conductivité globale augmente davantage. Le graphique à conservé est le graphique C.

3.  Le volume équivalent est de 11,6 mL. Les ions argent et chlorure sont alors dans les conditions stoechiométriques.

31 P 81 : Acide chlorhydrique commercial.

1. $H_{(aq)}^{ \ +} \ + \  HO^{ \ - }_{(aq)} \longrightarrow \ H_2O_{(l)}  $

2. Le volume équivalent est $V_E \ = \ 11,0 \ mL$.

3a.  $c_1 \times V_1 \ = \ c_B \times V_E$.

3b.  On en déduit : $c_1  \  =  \  \dfrac{ c_B \times V_E}{V_1} \ = \ \dfrac{1,00.10^{  \  -1} \times 11,0}{100} \ = \ 1,1.10^{  \  -2} \  mol/L $

4.  La solution $S_0$ ayant été diluée 1000 fois, $c_0 \ = \ 1000 \times c_1 \ = \ 1,1.10^{ \ 1} \ = \ 11,0 \ mol/L$.

5.  La masse $m_0$ de soluté dans la solution est donc : $m_0 \ = \ c_0 \times M(HCl) \ = \ 11,0 \times 36,5 \ = \ 401,5 \ g $.

6.  La masse $m$ de la solution est : $m \ = \ d \times V \times \rho _{eau} = 1,16 \times 1 \times 1000 \ = 1,16.10^{ \ 3} \ g $

7a. Le titre massique est donc : $w \ = \dfrac {401,5}{1,16.10^{ \ 3}} \ = \ 0,35$

7b. Le titre massique affiché est $w \ = \ 0,33$ MINIMUM. La valeur attendue est donc satisfaisante.

8. LPar la méthode des tangentes, on obtient un volume équivalent de 11 mL, identique à celui déterminé lors du dosage conductimétrique.

33 P 82 : Titrage du lait.

Partie 1.

1. La conductivité initiale de la solution est due aux ions contenus dans le lait.

2. Evolution de la conductivité de la solution lors du titrage : voir exercice 23.

3.  En traçant les deux demi-droites, on lit un volume équivalent : $V_E \ = \ 12 \ mL$.

4.  Les ions  réagissants sont versés dans les conditions stoechiométriques : $c_{Cl} \times V_1 \ =  \  c_2 \times V_E $. 

5.  On  en déduit : $c_{Cl} \ =  \ \dfrac {c_2 \times V_E }{V_1} = \dfrac {5,00.10^{ \ -3} \times 12 }{ 10} \ = \ 6,0.10^{ \ -3 } \ mol/L $.

Partie 2.

6a. Réaction : $AH_{(aq)} \ + \ HO_{(aq)}^{ \ -} \longrightarrow \ A^{ \ - }_{(aq)} \ + H_2O_{(l)}$.

6b. Les concentrations des réactifs doivent être minimes pour pouvoir observer correctement le saut de pH.

7a.  Volume équivalent :

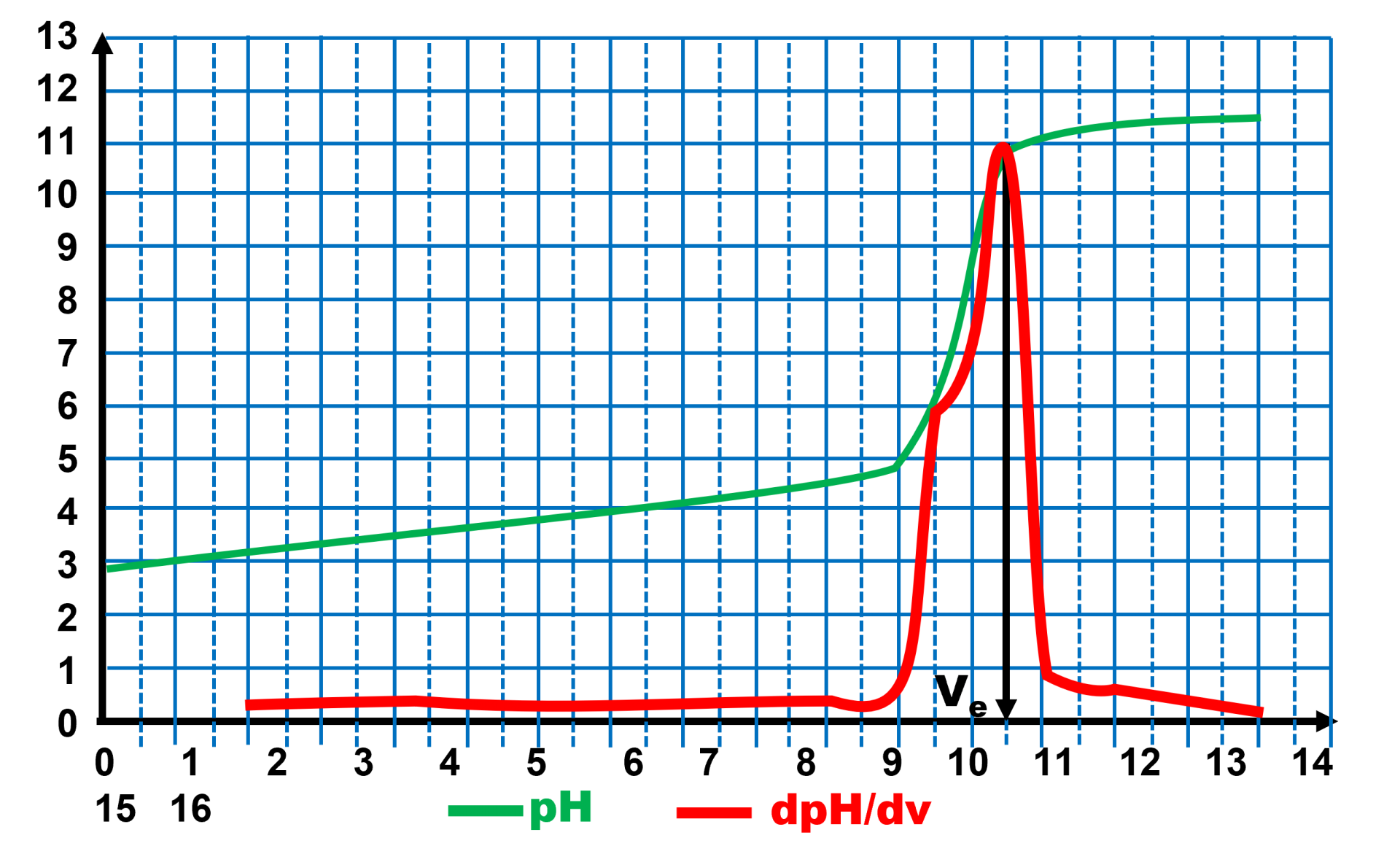7b.  Les ions  réagissants sont versés dans les conditions stoechiométriques : $n_{AH} =  \ c_B \times V_E \ = \ 5,00.10^{ \ -2} \times 10,5.10^{ \ -3} = 5,25.10^{ \ -4}  \ mol $.

8.  La masse d'acide lactique présent dans l'échantillon est donc : $m_{AH} \ =  \ n_{AH} \times M_{AH} = 5,25.10^{ \ -4} \times 90 \ = \ 4,73.10 ^{ \ -2} \ g$, dans un litre :$m_{AH} \left ( 1L \right )  \ = \ 4,73.10 { \ -2} \times 50 = 2,4 \ g$.

Le lait contient trop d'acide lactique, il n'est plus bon à la consommation.

9.  $\dfrac {u_m}{m} = \sqrt { \left ( \dfrac {U_{Ve}}{Ve} \right ) ^2 + \left ( \dfrac {U_{Va}}{Va} \right ) ^2 + \left ( \dfrac {U_{Cb}}{Cb} \right ) ^2} \ = \ \sqrt { \left ( \dfrac {0,1}{10,5} \right ) ^2 + \left ( \dfrac {0,1}{20,0} \right ) ^2 + \left ( \dfrac {10^{ \ -2}}{5,00.10^{ \ -2}} \right ) ^2} \ = \ 0,20 $.

Alors : $u_m \ = 0,20 \times 2,4 = 0,48 \ g$. Donc : $ m(1L) \ = \ 2,4 \pm 0,48 \ g : 1,92 \ \leq \ m(1L) \ \leq 2,88 \ g$

38 P 85 : Nettoyage chimique.

Analyse

1. La densité du vinaigre est $d \ = \ 1$. Donc : $d \ = \ \dfrac {\rho_{vin}}{\rho_{eau}}$ on en déduit : $\rho_{vin} \ = \ d \times \rho_{eau} \ = \ 1,0 \times 1000 \ = \ 1000 \ g/L $.

2. Protocole de dilution :

• Insérer une quantité suffisante de vinaigres dans un bécher propre et sec.

• Prélever les 10 mL souhaités à l'aide d'une pipette jaugée équipée d'une poire aspirante à 10 mL .

• Verser le contenu dans une fiole propre et sèche dans une fiole de 100 mL.

• Introduire de l'eau distillée au 1/3 de la fiole, uniformiser la solution en ayant fermé la fiole.

• Compléter la fiole à 100 mL et la fermer.

3. Réaction support :

$CH_3COOH_{(aq)} \ + \ HO^{ \ -}_{(aq)}  \ \ \ \longrightarrow \ \ \ CH_3COO^{ \ -}_{(aq)} \ + \ H_2O_{(l)} $

Synthèse

A l'équivalence, les réactifs sont dans les conditions toechimoétriques : $n_{acide} \ = n_{soude}$.

Soit : $c_{acide} \times v_{acide}  \ = \  c_{soude} \times v_{éq}$ donc :  $c_{acide} \ =  \ \dfrac {c_{soude} \times v_{éq}}{v_{acide}} \ = \ \dfrac {0,100 \times 13,3}{10,0} \ = \ 13,3.10^{ \ -2} \ mol.L^{ \ -1}$.

Il s'agit de la concentration de la solution diluée 10 fois. La concentration en acide dans le vinaigre est donc : $C \ = \ 13,3.10^{ \ -1} \ mol/L$

 La concentration massique est alors : $C_m \ = \ C \times M \ = 13,3.10 ^{ \ -1} \times 60 \ = \ 79,8 \ g/L $

Soit 7,98 g d'acide dans 100 mL de vinaigre. La valeur mesurée et en accord avec celle attendue.