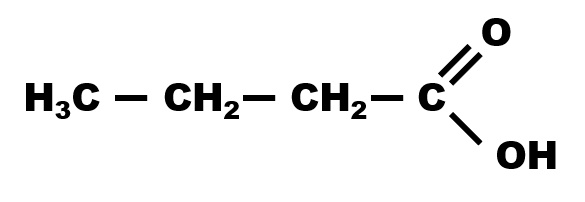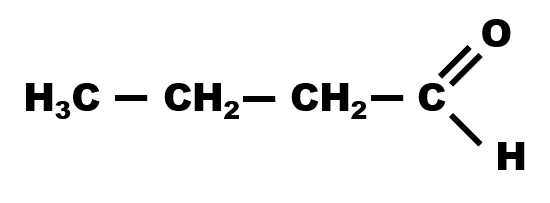Méthodes Physiques
10 P 51 : Qualité de l'eau d'une piscine.
1. $ \left [ H_3O_{(aq)} \right ] = 10^{-pH} = 10^{-7,4} = 4,0.10^{-8} \ mol.L^{-1}$
2. Le pH ayant augmenté, la solution est devenue plus basique, il suffira de l'acidifier, en ajoutant par exemple de l'acide chlorhydrique apportant des ions oxonium $H_3O^{ \ + }$.
12 P 51 : Boissons au cola.
1. $ 6,3 \times 10^{-5} \ mol.L^{-1} \lt \left [ H_3O_{(aq)}^{ \ + } \right ] \lt 3,2 \times10^{-3} \ mol.L^{-1}$
soit : $-log \left (3,2 \times10^{-3} \right ) \lt pH \lt-log \left ( 6,3 \times10^{-5} \right ) \ \ \Leftrightarrow \ 2,50 \ \lt pH \lt \ 4,2 $
3. Les deux valeurs de pH étant inférieures à 7, il s'agit de solutions acides.
15 P 51 :Colorant rouge.
|
1. |
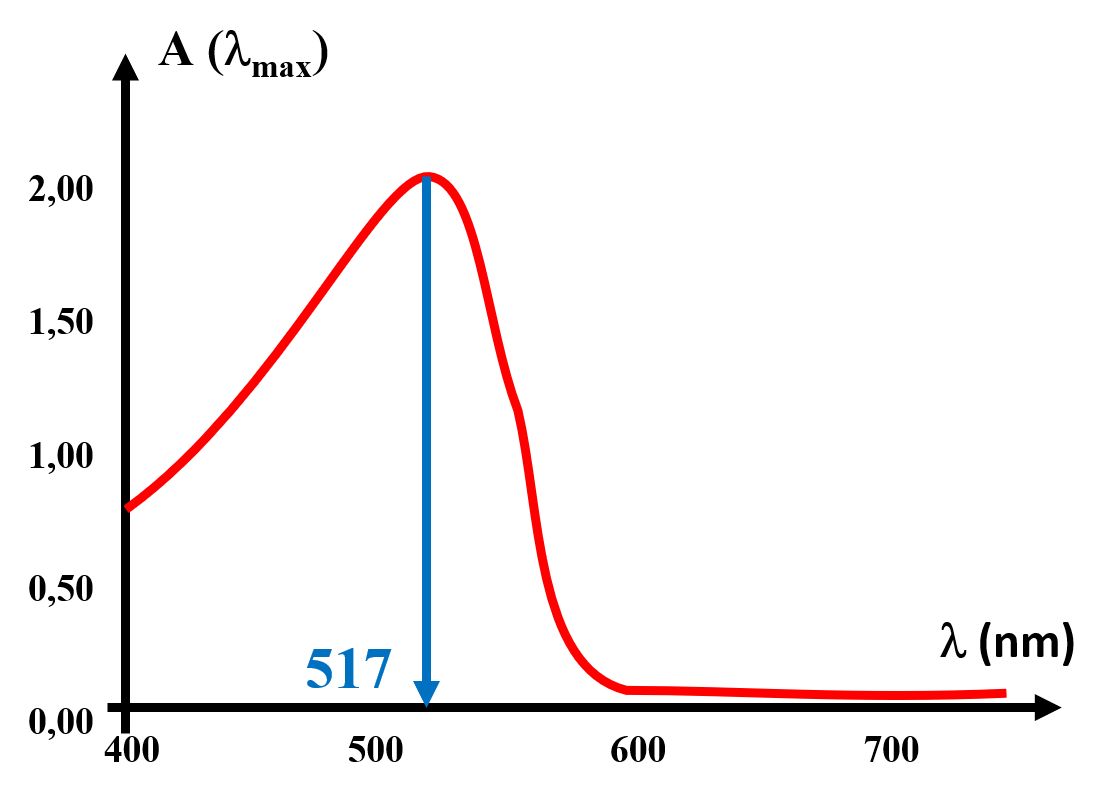 |
Le maximum d'absorbance se lit pour une longueur d'onde $\lambda _{max} \ = \ 517 nm$. 2. Il s'agit du "rouge Allura". |
16 P 52 : Sirop de menthe.
|
1. |
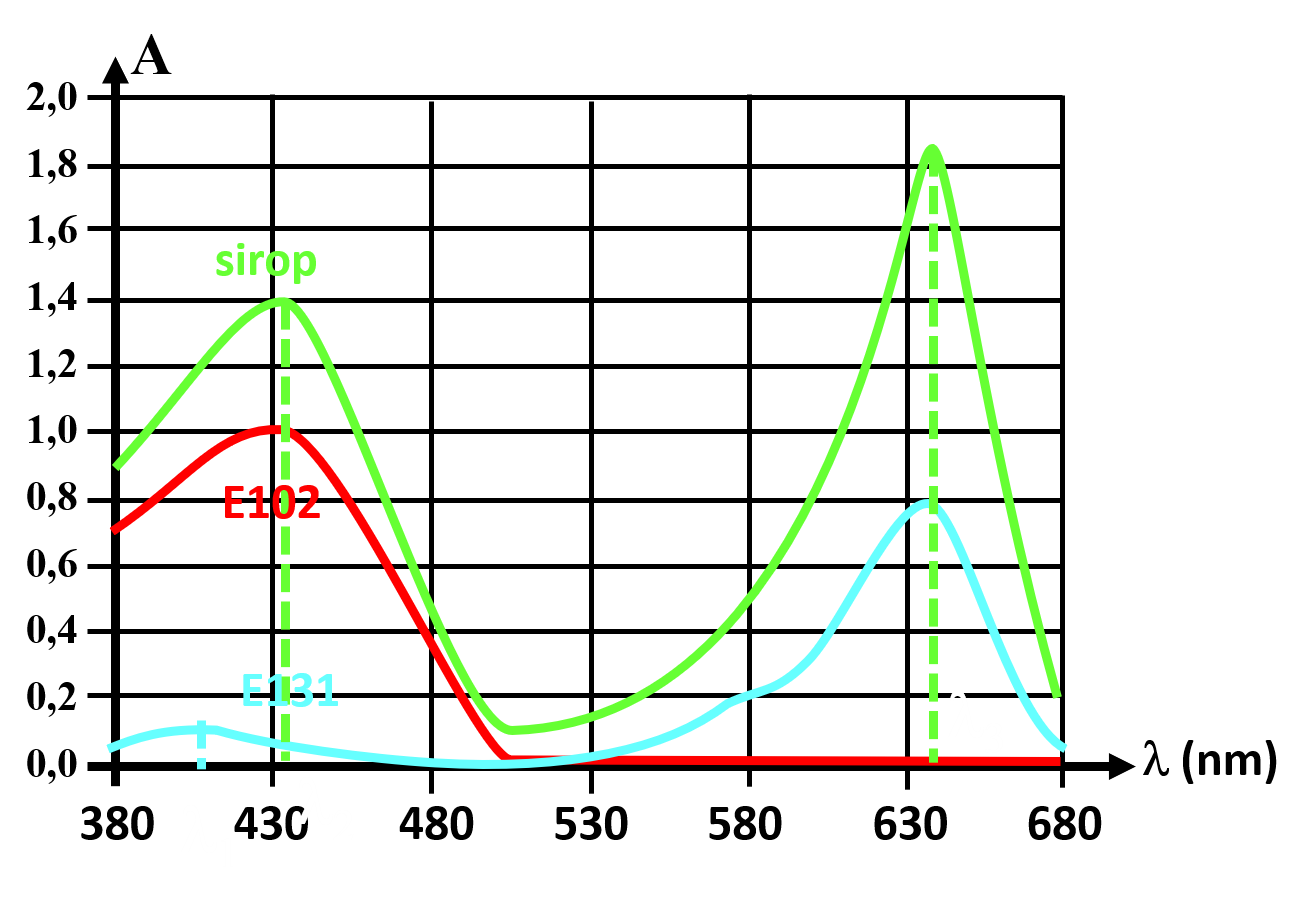 |
Pour le sirop, on lit deux maxima d'absorbance : $ \lamba _2 = 434 nm $ et $ \lamba _3 = 646 nm $ Pour le colorant E131, on lit deux maxima d'absorbance : $ \lamba _1 = 407 nm $ et $ \lamba _3 = 646 nm $ Pour le colorant E102, on lit un maximun d'absorbance : $ \lamba _3 = 646 nm $
|
2. Les maxima d'absorbance du sirop correspondent à la fois aux maxima d'absorbance des deux colorants E131 et E102. Sa couleur est donc due à un mélange de ces deux colorants (absorbant tous les deux dans le rouge et le bleu, ont observe bien une couleur verte).
19 P 52 : Association.
|
1. |
$H_3C - CH_2 - CH_2 - COOH$ Acide butanoïque
|
$H_3C - CH_2 - CH_2 - CHO$ Butanal
|
|||||||||||||||||||
|
2. |
|
||||||||||||||||||||
|
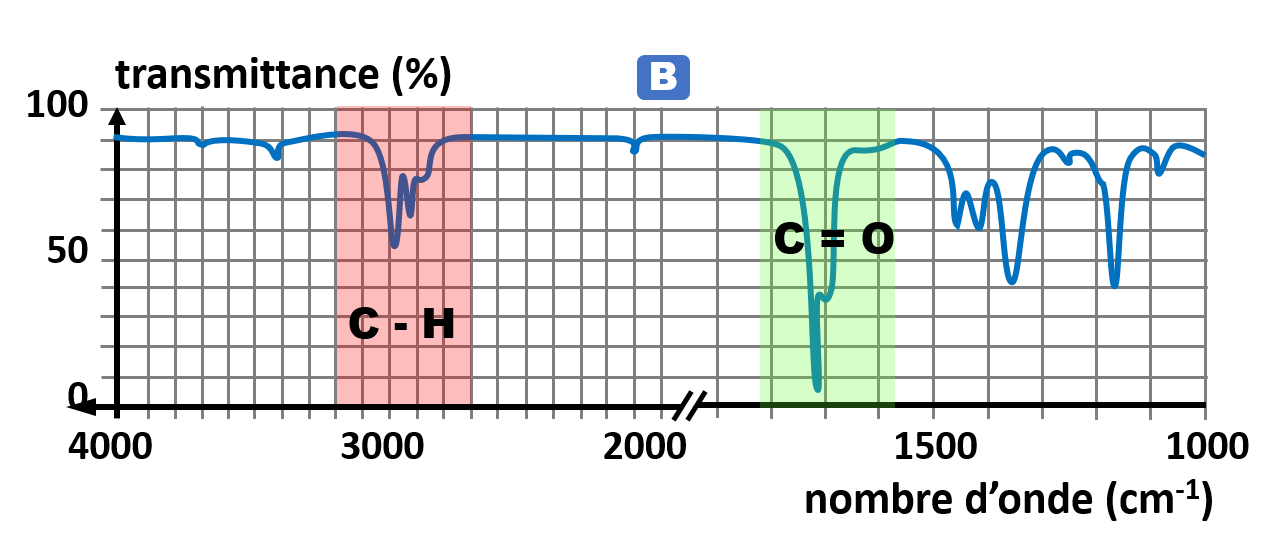
3. |
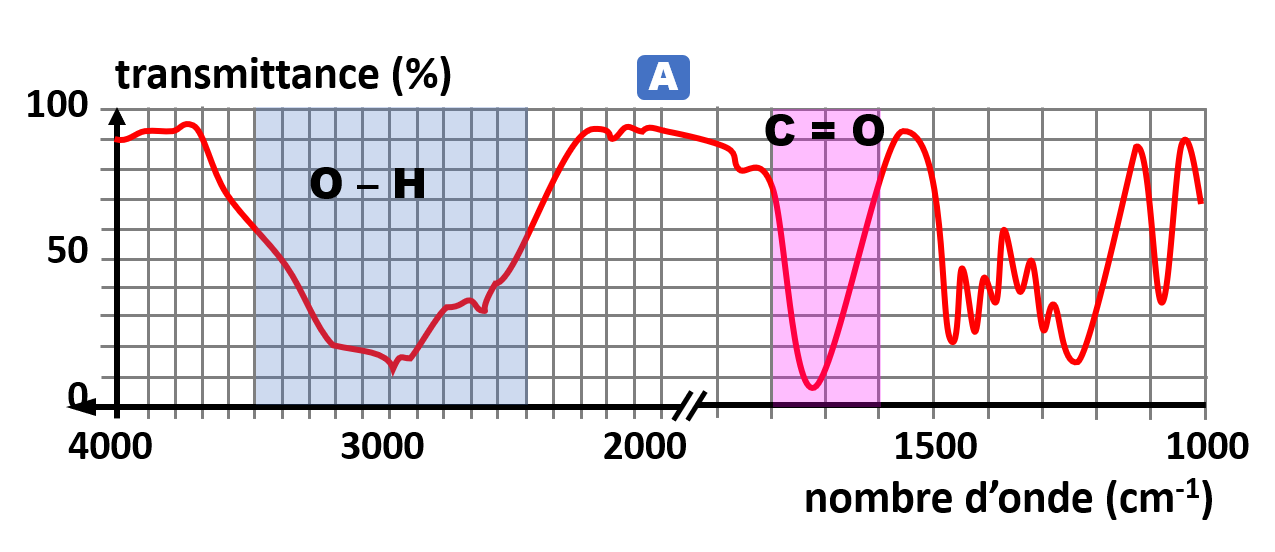
Il s'agit de l'aldéhyde : butanal. |
||||||||||||||||||||
20 P 52 : Gamme étalon.
1. Pour réaliser une dilution, on prélève précisément un volume V déterminé de la solution mère (avec une pipette jaugée) à la concentration C, qu'on introduit dans un récipient jaugé (fiole) qu'on complète avec de l'eau distillée.
2. La quantité de matière qui ne change pas est la quantité de matière introduite : $ n = C \times V$
3. La relation quantité de matière n'ayant pas changée $ n = C \times V$, la concentration de la solution finale est : $ C_f = \dfrac {n}{V_f} = \dfrac {C \times V}{V_f}$
| $V_m$ (en mL) de solution mère. | Volume $V_f$ (en mL) de solution fille. | Concentration $C_f$ de solution fille (en $mmol^{-1}$) |
| 10 | 50 |
$C_f = \dfrac {5\times 10^{-2} \times 10 \times 10 ^{-3}}{50 \times 10 ^{-3}} $ $C_f = 1,0 \times 10^{-2} mol.L^{-1} = 10 \ mmol.L^{-1}$ |
| 20 | 50 |
$C_f = \dfrac {5\times 10^{-2} \times 20 \times 10 ^{-3}}{50 \times 10 ^{-3}} $ $C_f = 2,0 \times 10^{-2} mol.L^{-1} = 20 \ mmol.L^{-1}$ |
| 30 | 50 |
$C_f = \dfrac {5\times 10^{-2} \times 30 \times 10 ^{-3}}{50 \times 10 ^{-3}} $ $C_f = 3,0 \times 10^{-2} mol.L^{-1} = 30 \ mmol.L^{-1}$ |
| 40 | 50 |
$C_f = \dfrac {5\times 10^{-2} \times 40 \times 10 ^{-3}}{50 \times 10 ^{-3}} $ $C_f = 4,0 \times 10^{-2} mol.L^{-1} = 40 \ mmol.L^{-1}$ |
21 P 53 : Dosage spectrophotométrique.
1. La longueur d'onde de réglage est choisie en utilisant le maximum d'absorbance d'une solution mère de la même espèce de concentration connue.
2.
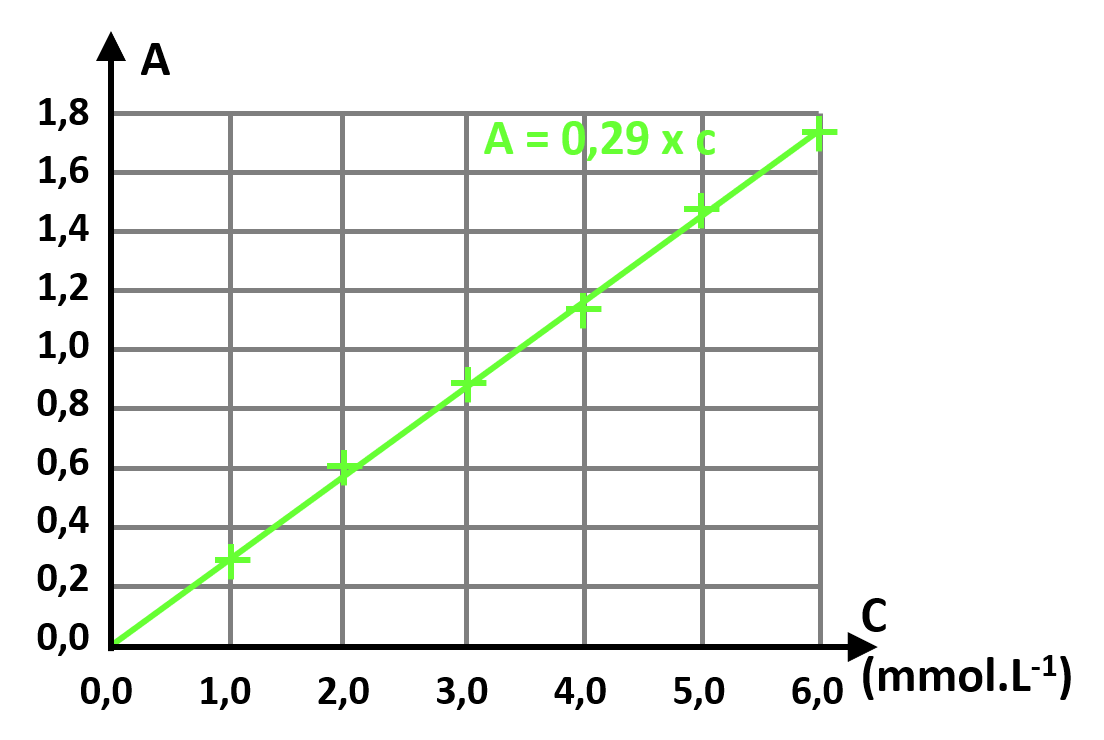
3. La courbe obtenue est une droite passant par l'origine : l'absorbance est proportionnelle à la concentration. On retrouve la loi de Beer-Lambert : $A = k \times C $
On détermine le coefficient directeur k graphiquement ou en utilisant un logiciel approprié.
4. $A =0,29 \times C $ pour une absorbance $A_s = 1,25 $, on en déduit : $c_s = \dfrac {1,25}{0,29} = 4,3 \ mmol.L^{-1}$
Ajouter un commentaire