Mouvement de Gravitation

14 P 327 : La planète naine Cérès.

1. L'aphélie et le périhélie étant tous deux supérieurs à la distance Terre-Soleil, Cérès est au-delà de la Terre.

Ceres2

3. Le demi-grand axe a pour valeur : $a_c \ = \ 4,47.10^{ \ 8} + 3,81.10^{ \ 8} \ = \ 8,28.10^{ \ 8} \ km$.

4. $\dfrac{T_c^2}{a_c^3} = \dfrac{T_T^2}{a_T^3} \ \Leftrightarrow \ T_c \ = \ T_T \sqrt{\left (\dfrac {a_T}{a_c} \right )^3}\ = \ 365,25 \times \sqrt{\left (\dfrac {1,5.10^{ \ 8}}{8,28.10^{ \ 8}} \right )^3} \ = \ 28,2 \ j$

15 P 327 : Les satellites de Saturne.

1. $\dfrac{T_1^2}{a_1^3} \ = \ \dfrac{T_2^2}{a_2^3} \ = \ \dfrac{4 \pi^2}{GM_S}$.

2. $T_1 \ = \ 2 \pi \times \sqrt{\dfrac{a_1^3}{GM_S}} \ = \ = \ T_2 \times \sqrt{\dfrac{a_1^3}{a_2^3}}$.

3. $T_{Encelade} \ = \ = \ T_{Thetys} \times \sqrt{\dfrac{a_{Encelade}^3}{a_{Thethys}^3}} \ = 1,89 \times \sqrt{\dfrac{0,238^3}{0,294^3}} \ = \ 1,38 \ j$

16 P 327 : La masse de Jupiter.

$M_J \ = \ \dfrac{4 \pi^2}{G} \times \dfrac{a^3}{T^2} \ = \ \dfrac{4 \pi^2}{6,67.10^{ \ -11}} \times \dfrac{(1,07.10^{ \ 9})^3}{(7,15 \ times 86400)^2} \ = \ 1,90.10^{ \ 27 } \ kg$

17 P 328 : Mouvement de la Terre autour du Soleil.

1. On se place dans le référentiel héliocentrique.

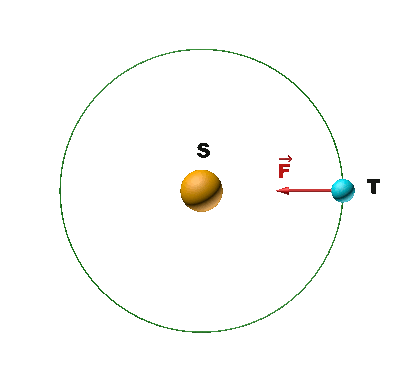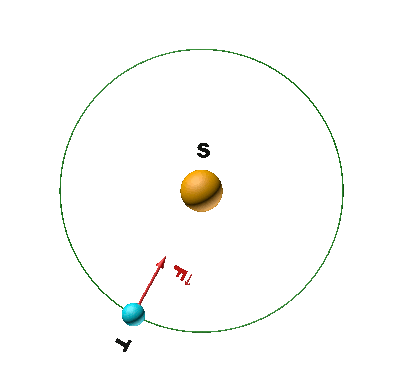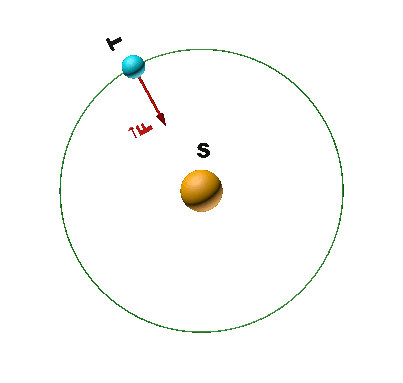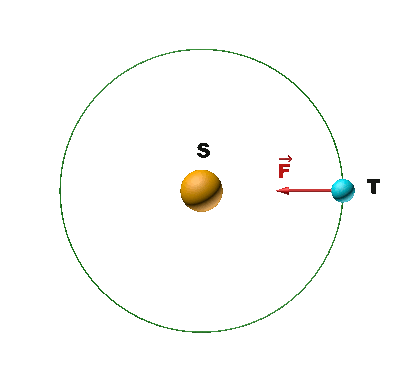$\overrightarrow {F_{S/T}} \ = \ - \dfrac {G.M_S.M_T}{d_{TS}^2} \times \overrightarrow {u_{S/T}}$

3. D'après la 2ème loi de Newton : $ \Sigma \overrightarrow F \ = \ M_T \times \overrightarrow a$.

Dans la base de Frenet cette relation s'écrit : $ \dfrac {G.M_S.M_T}{d_{TS}^2} \times \overrightarrow {u_n} \ = \ M_T \times \left ( \dfrac{dv}{dt} \overrightarrow {u_t} \ + \ \dfrac{v^2}{d_{TS}} \times \overrightarrow {u_n} \right )$

NB : $ \overrightarrow{u_{S/T}} \ = \ - \overrightarrow{u_n} $

Donc : $ \dfrac{G.M_S}{d_{TS}^2} \overrightarrow {u_n} \ = \ \dfrac{dv}{dt} \overrightarrow {u_t} \ + \ \dfrac{v^2}{d_{TS}} \times \overrightarrow {u_n}$

On en déduit que la composante $\dfrac{dv}{dt}$ selon le vecteur $\overrightarrow{u_t}$ est nulle.

Par conséquent, la vitesse étant constante, le mouvement est uniforme.

4. D'après la composante selon le vecteur $\overrightarrow {u_n}$, on a : $\dfrac{v^2}{d_{TS}} \ = \ \dfrac{G.M_S}{d_{TS}^2}$.

Soit : $v \ = \ \sqrt{\dfrac{G.M_S}{d_{TS}}} \ = \ \sqrt{\dfrac{6,67.10^{ \ -11} \times 1,99.10^{ \ 30}}{149,6.10^{9}}} \ = \ 2,98.10^{ \ 4} \ m.s^{ \ -1}$.

Autre méthode :

La Terre décrit une trajectoire circulaire de rayon $d_{TS}$,en une période $T \ = \ 3652,25 \ j$.

Sa vitesse est donc : $v \ = \ \dfrac {2 \pi \times d_{TS}}{T} \ = \ \dfrac { 2 \pi \times 149,6.10^{ \ 9}}{365,25 \times 86400} \ = \ 2,98.10^{ \ 4}\ m/s $.

5. D'après la troisième loi de Kepler : $\dfrac{T^2}{d_{TS}^3} \ = \ \dfrac{4 \pi^2}{M_S.G}$ soit : $T \ = \ \sqrt {\dfrac{4 \pi^2}{G.M_S} \times d_{TS}^3} \ = \ \sqrt {\dfrac{4 \pi^2}{6,67.10^{ \ -11} \times 1,99.10^{ \ 30 } } \times \left (149,6.10^{ \ 9} \right )^3} \ = \ 3,16.10^{ \ 7 } \ s$

Soit : $\dfrac{3,16.10^{ \ 7}}{86400} \ = \ 365,24 \ j$

18 P 328 : Les satellites GPS.

1. Dans le réferentiel géocentrique dont l'origine est le centre de la Terre et les trois axes dirigés vers des étoiles lointaines.

2. D'après la deuxième loi de Newton : $m \times \overrightarrow a \ = \ \Sigma \overrightarrow {F_{ext}}$

En se plaçant dans la base de Frenet liée au satellite, la force de gravitation de la Terre sur le satellite s'écrit : $\overrightarrow F = \dfrac{G.M_T.m}{\left ( R_t+h \right )^2} \times \overrightarrow {u_n}$

On a donc : $\dfrac{dv}{dt} \overrightarrow {u_t} \ + \ \dfrac{v^2}{\left ( R_T + h \right)^2} \times \overrightarrow {u_n} \ = \ \dfrac{G.M_T.m}{\left ( R_t+h \right )^2} \times \overrightarrow {u_n}$

On en déduit que :$\begin{cases} \dfrac{dv}{dt} \ = \ 0 \\ \dfrac{v^2}{R_T+h} \ = \dfrac{GM_T}{ \left ( R_T+h \right )^2} \end{cases}$

Donc : $v \ = \ \sqrt {\dfrac{GM_T}{R_T+h}}$

3a. Comme $\dfrac{dv}{dt} \ = \ 0$, le mouvement du saltellite est uniforme, sa vitesse est constante. Il parcourt son orbite circulaire de périmètre $2 \pi \left ( R_T+h \right )$ pendant sa période de révolution $T$.

Sa vitesse est alors : $v \ = \ \dfrac{2 \pi \left ( R_T+h \right )}{T}$

Donc : $\dfrac{2 \pi \left ( R_T+h \right )}{T} \ = \sqrt {\dfrac{GM_T}{R_T+h}}$

$\Leftrightarrow \ T \ = \ 2 \pi \left ( R_T+h \right ) \times \sqrt {\dfrac{R_T+h}{GM_T}}$

$\Leftrightarrow \ T \ = \ 2 \pi \times \sqrt {\dfrac{\left (R_T+h \right )^3}{G.M_T}}$

3b. AN : $ T \ = \ 2 \pi \times \sqrt {\dfrac{\left (6380.10^{ \ 3 }+1,36.10^{ \ 7} \right )^3}{6,67.10^{ \ -11} \times 5,97.10^{ \ 24}}} \ = \ 28543 \ s$

3c. Soit en 1 jour : $\dfrac{86400}{28543} \ = \ 3$ tours de la Terre

21 P 329 : Satellite géosynchrone et géostationnaire.

1. L'erreur serait : $\dfrac{|86400-86164|}{86400} \times 100 \ = \ 0,27 \ %$. On peut donc considérer que la période de révolution du satellite géosynchrone et celle de la Terre sont les mêmes.

2. $T \ = \ 2 \pi \sqrt {\dfrac{\left ( R_T+h \right )^3}{G.M_T}}$

$ \Leftrightarrow \ \sqrt {\dfrac{\left ( R_T+h \right )^3}{G.M_T}} \ = \ \dfrac{T}{2 \pi }$
$ \Leftrightarrow \ \dfrac{\left ( R_T+h \right )^3}{G.M_T} \ = \dfrac {T^2}{4 \pi^2}$
$\Leftrightarrow \ \left ( R_T+h \right )^3 \ = \  \dfrac {G.M_T \times T^2}{4 \pi^2}$
$\Leftrightarrow \  R_T+h \ = \ \left ( \dfrac {G.M_T \times T^2}{4 \pi^2} \right )^{\dfrac{1}{3}}$
$\Leftrightarrow \  h\ = \ \left ( \dfrac {G.M_T \times T^2}{4 \pi^2} \right )^{\dfrac{1}{3}} - R_T$

AN : $h \ = \ 35770 \ km$

3a. La figure 2 n'est pas compatible avec la deuxième loi de Newton : la force d'attraction de la Terre est dirigée selon la droite Centre de la Terre $\rightarrow$ Satellite. L'accélération doit suivre cette même direction. Dans la situation proposée, la direction de l'accélération n'aurait pas cette direction, elle serait dirigée du satellite vers le pôle.

3b. Les deux situations répondant à cette condition sont représentées dans la figure 1 et la figure 2.

4a. Son plan de rotation serait le plan de l'équateur.

4b. Son sens de rotation serait le même que celui de la Terre autour de son axe de rotation.

4c. Figure 1.