Phénomènes ondulatoires

Exercice n°8 P441 : Plus on est nombreux....

1a. La mesure du niveau d'intensité sonore s'effectue avec un sonomètre.

1b. L'intensité sonore d'une guitare est : $I \ = \ I_0 \times 10^{\dfrac{L}{10}}$

Pour $n$ guitares, le niveau d'intensité sonore sera : $I_n \ = \ n \times I$

Le niveau d'intensité sonore sera : $L_n \ = \ 10 \times log \left ( \dfrac{I_n}{I_0} \right ) \ = \ 10 \times log \left ( \dfrac{n \times I}{I_0} \right )$

Soit : $L_n \ = \ 10 \times \left ( log(n) + log \dfrac {I}{I_0} \right ) \ = \ 10 \times log (n) + 10 log \dfrac{I}{I_0}$.

Alors : $L_n \ = \ 10 \times log(n) + L_1 \  \ \Leftrightarrow \ \ 10 \times log (n) \ = \ L_n \ - \ L_1$.

$\Leftrightarrow \ \ log(n) \ = \dfrac {L_n - L_0}{10}$

$n \ = 10^{\dfrac {L_n - L_0}{10}} \ = \ 10^{\dfrac {75-65}{10}} \ = \ 10 \ guitares$

2.

L'intensité sonore est : $I_{tot} \ = \ I_{guitares} \ + \ I_{triangle} \ = \ I_0 \times \left ( 10^{ \ 75/10}+10^{ \ 50/10} \right )$

Le niveau d'intensité sonore est donc : $L_{tot} \ = \ 10 \times log \dfrac {I_0 \times \left ( 10^{ \ 75/10}+10^{ \ 50/10} \right ) }{I_0} \ = \ 10 \ \times log \left(10^{ \ 7,5} + 10^{ \ 5} \right ) \ = \ 75 \ db$

Exercice n°10 P441 :Santé au travail.

1.

$I_1 \ = \ I_0 \times 10^{\dfrac{L_1}{10}} \ = \ 1,0.10^{ \ - 12 } \times 10^{83/10} \ = \ 2,0.10^{ \ -4} \ W.m^{ \ -2}$

$I_2 \ = \ I_0 \times 10^{\dfrac{L_2}{10}} \ = \ 1,0.10^{ \ - 12 } \times 10^{823/10} \ = \ 1,6.10^{ \ -4} \ W.m^{ \ -2}$

2a.

$L \ = \ 10.log \left ( \dfrac{I_1+I_2}{I_0} \right ) \ = \ 10.log \left ( \dfrac{3,6.10^{ \ -4}}{1,0.10^{ \ -12}} \right ) \ = \ 85,6 \ dB$

2b.

$85,6 \ < \ 87 \ dB$ : ça le fait pour le patron !

Exercice n°12 P441 : Expérience de la diffraction d'ondes lumineuses.

1.

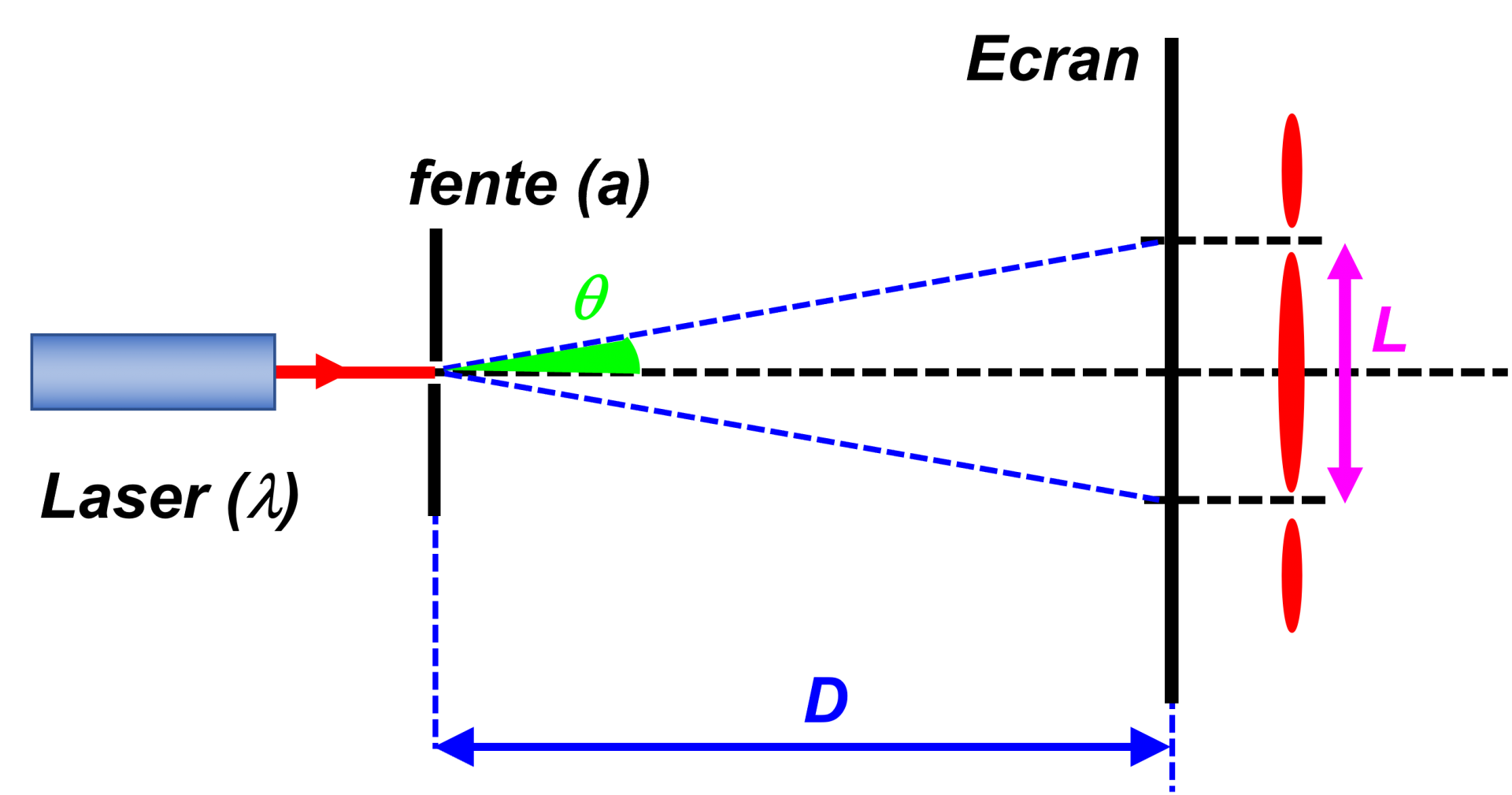
2a.

$\fbox{$\theta \ = \dfrac{\lambda}{a}$}$

$\theta$ : angle de diffraction en radians ; $\lambda$ : longueur d'onde de la source en mètre ; $a$ : largeur de la fente en mètre.

2b.

D'après le schéma : $tan \theta \ = \ \dfrac{L/2}{D} \ = \ \dfrac{L}{2D}$

Comme $tan \theta \ = \ \theta$ : $\theta \ = \ \dfrac{L/2}{D} \ = \ \dfrac{L}{2D}$

Soit: $\fbox{$\theta \ = \dfrac{\lambda}{a} \ = \ \dfrac{L}{2D}$}$

Exercice n°14 P442 : Diffraction des ondes à la surface de l'eau.

 1.

Après la fente de diffraction, nous avons mesuré 6 longueurs d'onde pour 5 cm. Donc : $\lambda \ = \ \dfrac {5,0}{6} \ = \ 0,83 \ cm$

De la même façon, avant la fente de diffraction, on mesure 4 longueurs d'onde pour 3,4 cm. Donc : $\lambda \ = \ \dfrac {3,4}{6} \ = \ 0,85 \ cm$

On peut en conclure que la diffraction ne modifie pas la longueur d'onde.

 2.

On mesure une largeur de fente $a \ = \ 6,0 \ mm$.

L'angle de diffraction est : $\theta \ = \ \dfrac{\lambda}{a} \ = \ \dfrac{0,83.10^{ \ 2}}{6,.10^{ \ -3}} \ = \ 1,34 \ rad$ soit : $\theta \ = 1,34 \times \dfrac{180}{\pi} \ = 77^°$.

Ce qui est cohérent avec la mesure effectuée en utilisant "Tracker".

Exercice n°16 P441 : Interférences sonores.

1a.

Le point est situé à 1 m de la source. Il se trouve à une demi longueur d'onde. Il est situé à 4 m de la source. Il se trouve à deux longueurs d'onde. Les ondes arrivant en ce point sont en opposition de phase. En ce point, l'amplitude sera donc minimale.

1b.

Ondes destructives.

2.

Cette fois, le point est situé à 3 longueurs d'onde de la première source et à 7 longueurs d'ondes de la deuxième source. Les ondes sont en phase en ce point. L'amplitude y sera maximale. On parle d'ondes constructives.

Exercice n°17 P442 : Superposition d'ondes.

1.

Issues de la même sources, les ondes sont cohérentes.

2,3.

Dans ce cas, les ondes sont en opposition de phase. Les interférences sont destructives. Zone sombre dans le cas d'ondes lumineuses. Aucun son dans le cas d'ondes sonores. Dans ce cas, les ondes sont en  phase. Les interférences sont constructives. Zone éclairée dans le cas d'ondes lumineuses. Un son maximum dans le cas d'ondes sonores. Dans ce cas, les ondes sont en opposition de phase.  Zone peu éclairée dans le cas d'ondes lumineuses. Un son atténué dans le cas d'ondes sonores

Exercice n°18 P442 : Différence de chemin optique.

1a.

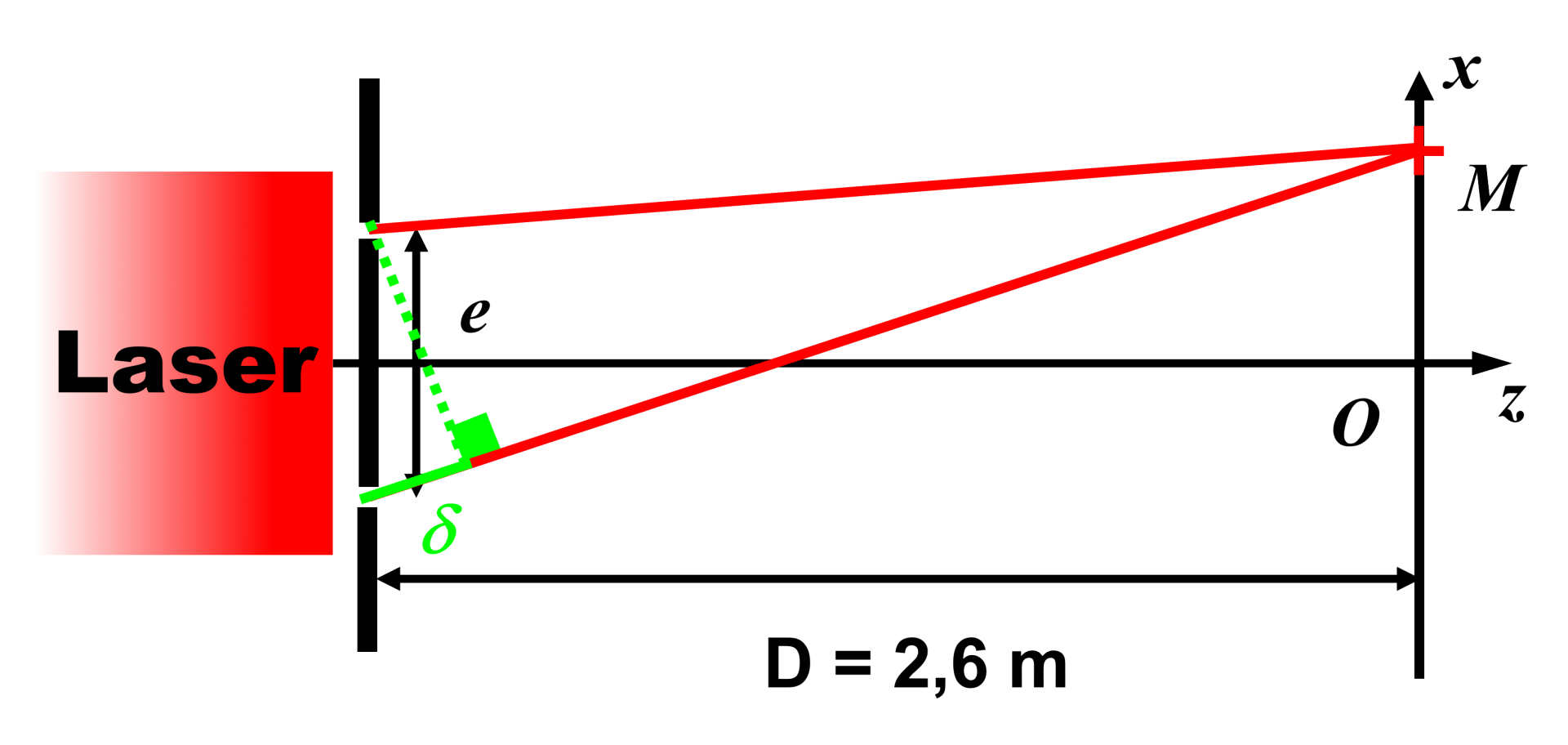
La différence de chemin optique est la différence des distances parcourues par les faisceaux provenant des deux fentes pour arriver en M.

1b.

Pour atteindre le point O, les fentes étant symétriques par rapport à l'axe $(Oz)$, le différence de chemin optique est nulle. Les deux ondes arrivant en M ont parcouru la même distance. La différence de chemin aoptique est nulle. Elles arrivent en M dans le même état. Elles y sont donc en phase. Le point O est sur une frange brillante.

2.

Pour que le point M soit sur un point brillant, il faut que la différence de chemin optique soit un multiple de la longueur d'onde : $\delta \ = \ k \times \lambda$. Pour que ce soit le premier point brillant :$\delta \ = \ 1 \times \lambda \ = \ \lambda \ = \dfrac{e.x}{D} $ soit : $x \ = \ \dfrac{\delta .D}{e}$

3.

$x \ = \ i \ = \dfrac{\delta .D}{e} \ = \ \dfrac{\lambda . D}{e} $

4.

$ i \ = \dfrac{\delta .D}{e} \ = \ \dfrac{\lambda . D}{e} $, donc : $e \ = \dfrac{\lambda .D}{i} \ = \ \dfrac{633.10^{ \ -9}\times .2,6}{3,4.10^{ \ -3}} \ = \ 4,8.10^{ \ -4} \ m \ = \ 0,48 \ mm$

Exercice n°22 P444 : Diffraction dans un télescope.

1,2.

La différence s'observe lors de la rencontre d'une onde sinusoïdale avec un obstacle ou une fente. Elle est due à "l'éclatement" de cette onde lors de cet obstacle. Pour une onde lumineuse, c'est le caractère sinusoïdal de cette onde qui induit que les lois de la géométrique ne sont plus applicables.

3.

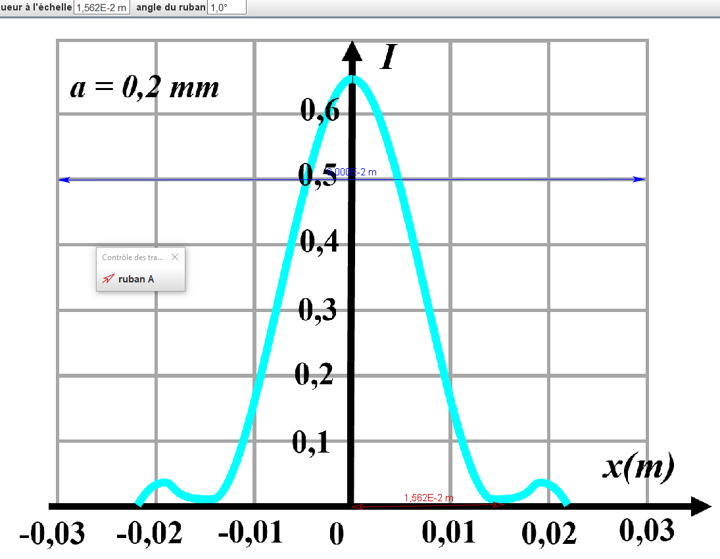
On mesure une première extinction à la distance $x_1 \ = 1,6.10^{ \ -2} \ m$

Le diamètre de la tâche est donc : $d_{Airy} \ = \ 2.x_1 \ = \ 3,2.10^{ \ -2} \ m$

Exercice n°28 P447 : Additionner sans calculatrice.

1.

La fonction mathématique modélisant le niveau d'intensité sonore est le logarithme décimal : $L_{dB} \ = \ 10 \times log \dfrac {I}{I_0}$. Les niveaux d'intensité sonore ne peuvent pas s'ajouter car $log(a) + log(b) \ \ne \ log(a+b)$

2a,b.

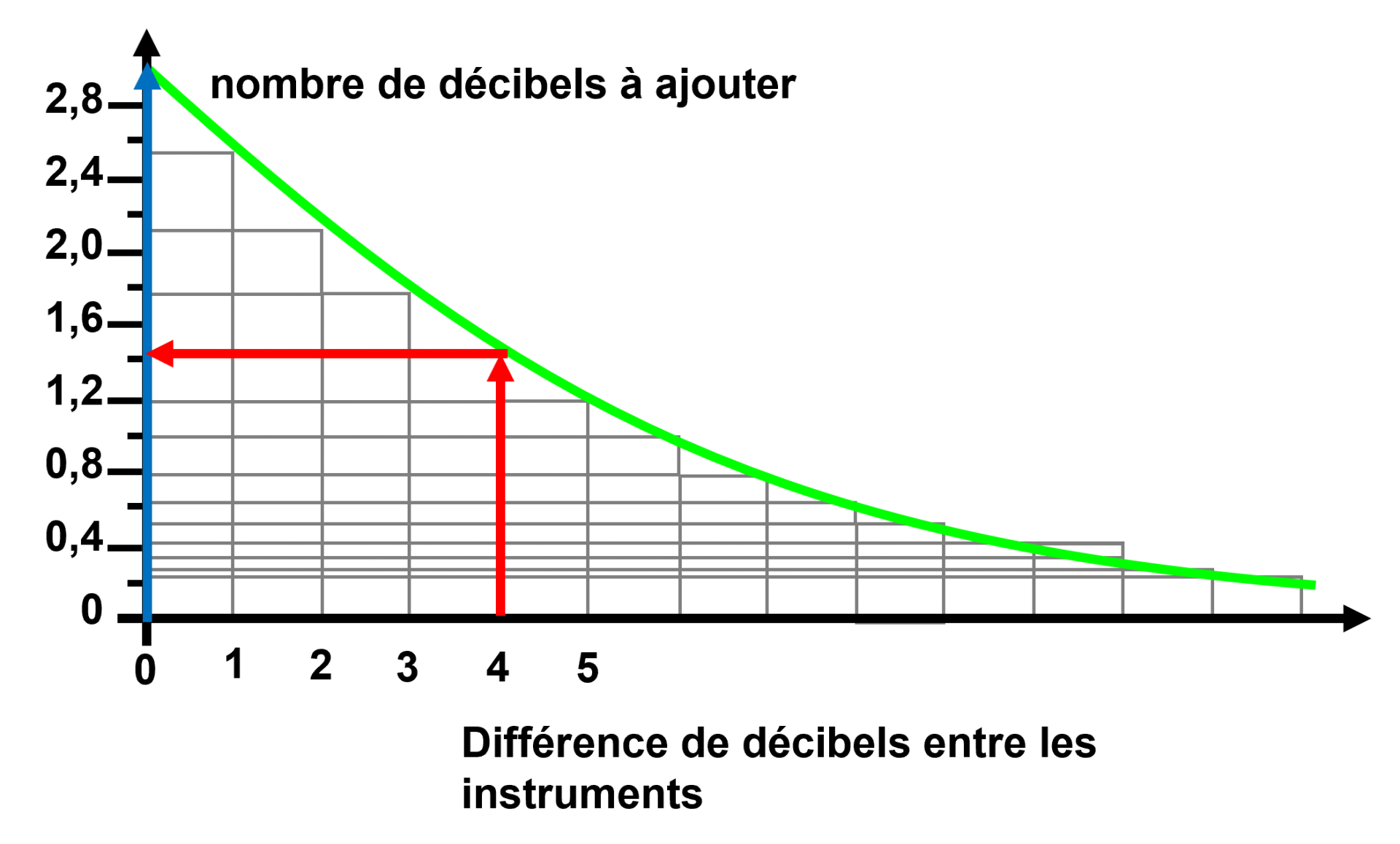
Dans le premier cas, la différence de niveau sonore entre les deux instruments est de 4 dB. Le niveau sonore total sera de $87 + 1,4 \ = 88,4 \ db$

Dans le premier cas, la différence de niveau sonore entre les deux instruments est de 0 dB. Le niveau sonore total sera de $82 + 3 \ = 85 \ db$

Exercice n°29 P447 : Interférences et rayons X.

Pour observer une interférence entre les faisceaux réfléchis par deux atomes situés sur chacun des plans, il faut que la différence de marche entre les rayons soit un multimple de la longueur d'onde : $\delta = k \times \lambda$.

La première interférence s'observera à $\delta \ = \ 1 \times \lambda \ = \ \lambda$

Soit : à $\delta \ = 2d.sin \theta \ = \lambda \ \Leftrightarrow \ d \ = \ \dfrac{\lambda}{2.sin \theta} $

AN : $d \ = \ \dfrac{145}{2.sin 11,5} \ = \ 364 \ pm$