Physique Nucléaire

Exercice n°14 P 123 : Problème de stabilité.

1.

La radioactivité consiste en la désintégration d'un noyau lourd en un noyau plus léger et en l'émission d'une particule légère, $\alpha \ , \ \beta ^{ \ +} \ ou \ \beta ^{ \ -}$.

Exercice n°15 P 123 : Equations.

1.

Lors d'une réation nucléaire, on a conservation :

- de la charge.

- du nombre de nucléons.

2a.

$^{\color{blue}{210}}_{\color{red}{84}} \color{black}{Po} \longrightarrow \ ^{\color{blue}{206}}_{\color{red}{82}}\color{black}{Pb} \ + \ ^{\color{blue}{4}}_{\color{red}{2}}\color{black}{He}$

$\color{blue}{210} \ = \ \color{blue}{206} \ + \ \color{blue}{4}$

$\color{red}{84} \ = \ \color{red}{82} \ + \ \color{red}{2}$

La réaction est équilibrée.

2b.

$^{\color{blue}{7}}_{\color{red}{4}} \color{black}{Be} \ + \ ^{\color{blue}{1}}_{\color{red}{1}} \color{black}{H} \longrightarrow \ ^{\color{blue}{4}}_{\color{red}{2}}\color{black}{He}$

$\color{blue}{7} \ + \ \color{blue}{1} = \ 2 \times \color{blue}{4} \ $

$\color{red}{4} \ + \ \color{red}{1} \ \neq \ 2 \times \ \color{red}{2}$

La réaction n'est pas équilibrée.

2c.

$^{\color{blue}{235}}_{\color{red}{92}} \color{black}{U} \ + \ ^{\color{blue}{1}}_{\color{red}{0}} \color{black}{n} \longrightarrow \ ^{\color{blue}{139}}_{\color{red}{54}}\color{black}{Xe} \ + \ ^{\color{blue}{94}}_{\color{red}{38}}\color{black}{Sr} \ + \ ^{\color{blue}{1}}_{\color{red}{0}}\color{black}{n}$

$\color{blue}{235} \ + \ \color{blue}{1} \neq \ \color{blue}{139} \ + \ \color{blue}{94} \ + \ \color{blue}{1}$

$\color{red}{92} \ + \ \color{red}{2} \ = \ \color{red}{54} \ + \ \color{red}{38} \ + \ \color{red}{0}$

La réaction n'est pas équilibrée.

2d.

$\color{blue}{9} \ + \ \color{blue}{4} \neq \ \color{blue}{12} $

$\color{red}{4} \ + \ \color{red}{2} \ = \ \color{red}{6}$

La réaction n'est pas équilibrée.

Exercice n°16 P 123 : Le potassium 40, $^{40}_{19}K$

1,2.

Dans toute réaction nucléaire, il a conservation de la charge.

Dans le cas de la transformation en calcium 40 $^{40}_{20}Ca$, la particule émise doit être égale à $-1$.

La particule émise est un électron $^0_{-1}e$.

$^{40}_{19}K \longrightarrow ^{40}_{20}Ca \ + \ ^0_{-1}e$

Dans le cas de la transformation en argon 40 $^{40}_{18}Ca$, la particule émise doit être égale à $+1$.

La particule émise est un positon$^0_{1}e$.

$^{40}_{19}K \longrightarrow ^{40}_{18}Ar \ + \ ^0_{1}e$

Exercice n°19 P 124 : Carbone 14

1.

Pour 200g d'os, on observe 15 désintégrations par minute. L'activité est : $\dfrac{15}{60} \ = \ 0,25 \ Bq$

2a.

$A(t) \ = \ - \ \dfrac{dN(t)}{dt} \ = \ \lambda \times N(t)$

Soit : $ \boxed{ \ \ \ \dfrac{dN(t)}{dt} \ + \ \lambda \times N(t) \ = \ 0 \ \ \ }$

2b.

Si $N(t) \ = \ N_0 \times e^{ \ - \lambda .t}$, on a : $\dfrac{dN(t)}{dt} \ = \ - \lambda \times N_0 \times e^{ \ - \lambda .t}$

Alors : $\dfrac{dN(t)}{dt} \ - \ \lambda \times N(t) \ = \ \lambda \times N_0 \times e^{ \ - \lambda .t} - \lambda \times N_0 \times e^{ \ - \lambda .t} \ = \ 0$ CQFD

3.

L'expression de l'activité est donc : $A(t) \ = \ - \ \dfrac{dN(t)}{dt} \ = \ \lambda \times N_0 \times e^{ \ - \lambda .t}$

$N(t) \ = \ \dfrac{A(t)}{\lambda} \ = \ \dfrac{0,25)}{3,93.10^{ \ -12}} \ = \ 6,63.10^{ \ 10}$

Exercice n°20 P 124 : Elément radioactif.

1.

$\dfrac{dN(t)}{dt} \ = \ - \lambda \times N(t)$, l'expression de $N(t)$ est donc : $N(t) \ = \ A \times e^{- \lambda .t}$

A $t=0$, $N(0) \ = \ N_0 \ = \ A \times e^{- \lambda .0} \ = \ A$

Alors : $N(t) \ = \ N_0 \times e^{- \lambda .t}$

2a.

Le temps de demi-vie $t_{1/2}$ est le temps au bout duquel la quantité vérifie : $N(t_{1/2}) \ = \ \dfrac{N_0}{2}$

2b.

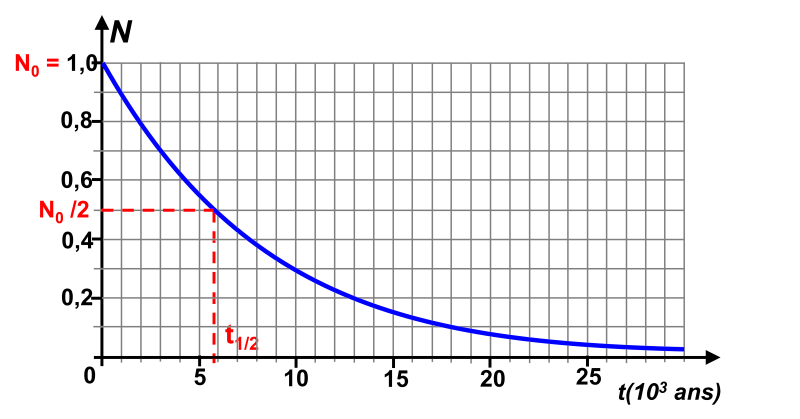
On détermine graphiquement : $t_{1/2} \ = \ 5,85.10^{ \ 3} \ ans$

2c.

Il s'agit du carbone 14.

3a.

A $t \ = \ t_{1/2} \ , \ N(t_{1/2}) \ = \ \dfrac{N_0}{2}$

$\Leftrightarrow \ \dfrac{N_0}{2} \ = \ N_0 \times e^{- \lambda .t_{1/2}}$

$\Leftrightarrow \ \dfrac{1}{2} \ = \ e^{- \lambda .t_{1/2}}$

$\Leftrightarrow \ ln \left ( \dfrac{1}{2} \right ) \ = \ - \lambda .t_{1/2}$

$\Leftrightarrow \ \color{red}{\lambda \times t_{1/2} \ = \ ln(2)}$

3b.

$\lambda \ = \ \dfrac{ln(2)}{t_{1/2}} \ = \ \dfrac{ln(2)}{5,85.10^{ \ 3}} \ = \ 1,2.10^{ \ -4} \ an^{ \ -1}$

Exercice n°23 P 125 : Datation d'un drakkar.

1.

Une fois mort, le carbone 14 présent naturellement dans le bois n'est plus régénéré, sa quantité diminue.

2a.

$A(t) \ = \ A_0 \times e^{ \ - \lambda . t}$

$\Leftrightarrow \ e^{ \ - \lambda . t} \ = \ \dfrac{A(t)}{ A_0}$

$\Leftrightarrow \ - \lambda . t \ = \ ln \left ( \dfrac{A(t)}{ A_0} \right )$

$\Leftrightarrow \ t \ = \ \dfrac{1}{\lambda} \times ln \left ( \dfrac{A_0}{ A(t)} \right )$

2b.

$AN \ : \ t \ = \ \dfrac{1}{3,87.10^{ \ -12}} \times ln \left ( \dfrac{13,6}{12} \right ) \ = \ 3,23.10^{ \ 10} \ s$

Soit : $ \dfrac{3,23.10^{ \ 10}}{86400 \times 365,25} \ = \ 1025 \ ans$

L'année de construction est donc : $1983 \ - \ 1024 \ = 985$

Exercice n°26 P 126 : Séisme californien.

1.

$^{14}_6 C \longrightarrow \ ^{0}_{-1} e + ^{14}_7 N$

2.

L'activité d'un échantillon radioactif correspond au nombre de désintégrations par seconde. Elle s'exprime en Becquerel (Bq).

3.

L'activité mesurée est $A \ = \ 0,223$. On a : $A(t) \ = \ A_0 \times e^{ \ - \lambda . t}$

Donc (voir exercice précédent) $t \ = \ \dfrac{1}{\lambda} \times ln \left ( \dfrac{A_0}{ A(t)} \right ) \ = \ \dfrac{1}{1,22.10^{ \ -4}} \times ln \left ( \dfrac{0,255}{ 0,223} \right ) \ = \ 1099 \ ans $

Le séisme a eu lieu en : $1989 \ - \ 1099 \ = 890$

Exercice n°28 P 127 : Détection par un compteur de radioactivité.

1.

La relation : $\dfrac{dN(t)}{dt} \ = \ - \lambda \times N(t)$ est une équation différentielle du premier ordre dont la solution générale est : $N(t) \ = \ N_0 \times e^{ \ -\lambda . t}$ où $N_0$ représente la quantité de matière radioactive à l'instant $t \ = \ 0$.

2.

Le temps de demi-vie $t_{1/2}$ est la durée nécessaire à la disparition de la moitié de la quantité de matière considérée à l'instant choisi comme référence.

3.

Sur le graphique, on constate que le bismuth 214 se décompose plus rapidement que le plomb 214. Sa constante de demi-vie est plus courte.

La constante de radioactivité $\lambda$ est donc plus grande pour le bismuth 214 (vite au cours de mathématiques pour cette justification "exponentiellement" rapide)

NB : aucune valeur numérique n'est demandée, libre à vous de les déterminer en utilisant le graphique fourni dans l'énoncé.

Exercice n°32 P 129 : Un gaz méconnu.

1.

Première désintégration $\alpha$ : $^{234}_{92} U \ \longrightarrow \ ^{230}_{90} Th \ + \ ^{4}_{2} He$

Deuxième désintégration $\alpha$ : $^{230}_{90} Th \ \longrightarrow \ ^{226}_{88} Ra \ + \ ^{4}_{2} He$

Troisième désintégration $\alpha$ : $^{226}_{88} Ra \ \longrightarrow \ ^{222}_{86} Rn \ + \ ^{4}_{2} H$e

2.

Sur le même intervalle de mesure, on calcule un nombre de désintégrartion moyen : $\overline{n_d} \ = \ \dfrac{\sum {n_d}}{N} \ = \ 8,05$ désintégrations.

L'écart-type est : $\sigma_n \ = \ 3,07$

L'incertitude-type est : $u_n \ = \ \dfrac{\sigma_n}{N} \ = \ 0,69$

On estime au mieux, le nombre de désintégrations $n_d$ à : $n_d \ = \ 8,05 \ \pm \ 0,69$ désintégrations.

3.

L'activité moyenne $\overline A$ est donc : $\overline A \ = \ 80 \times 8,05 \ = \ 644 \ Bq.m^{ \ -3}$, supérieure à la norme européenne.

Exercice n°34 P 129 : protection contre les rayonnements.

1.

On détermine graphiquement une couche de demi-atténuation : $e = 0,4 \ mm$

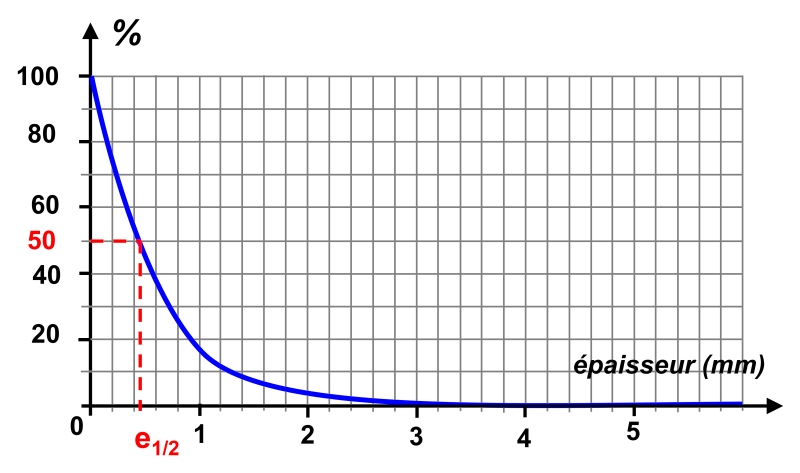
2.

Avec une épaisseur de $5 \ mm$, les rayonnements $\gamma$ sont totalement bloqués.

Exercice n°35 P 129 : Tomographie par émission de positons.

1.

Désintégration $\beta ^{ \ +}$ de l'oxygène 15 : $^{15}_{8} O \ \longrightarrow \ ^{15}_{7} N \ + \ ^{0}_{1} e$

2.

Le temps de demi-vie $t_{1/2}$ est la durée nécessaire à la disparition de la moitié de la quantité de matière considérée à l'instant choisi comme référence.

3a.

Loi de décroissance radioactive : $N(t) \ = \ N_0 \times e^{ \ -\lambda \times t}$

Au temps de demi-vie : $N(t_{1/2}) \ = \ \dfrac{N_0}{2}$

$\Leftrightarrow \ \dfrac{N_0}{2} \ = \ N_0 \times e^{- \lambda .t_{1/2}}$

$\Leftrightarrow \ \dfrac{1}{2} \ = \ e^{- \lambda .t_{1/2}}$

$\Leftrightarrow \ ln \left ( \dfrac{1}{2} \right ) \ = \ - \lambda .t_{1/2}$

$\Leftrightarrow \ \lambda \times t_{1/2} \ = \ ln(2)$

$\Leftrightarrow \ \color{red}{\lambda \ = \ \dfrac{ln(2)}{t_{1/2}}}$

3b.

AN : $\lambda \ = \ \dfrac{ln(2)}{t_{1/2}} \ = \ \dfrac{ln(2)}{123} \ = \ 5,6.10^{ \ -3} \ s$

4.

On cherche l'instant $t_1$ pour lequel : $N(t_1) \ = \ 0,05 \times N_0$

$\Leftrightarrow \ 0,05 \times N_0 \ = \ N_0 \times e^{- \lambda .t_1}$

$\Leftrightarrow \ \dfrac{5}{100} \ = \ e^{- \lambda .t_1}$

$\Leftrightarrow \ ln \left ( \dfrac{5}{100} \right ) \ = \ - \lambda .t_1$

$\Leftrightarrow \ t_1 \ = \ \dfrac{1}{\lambda} \times ln \left ( \dfrac{100}{5} \right ) $

AN : $t_1 \ = \ 532 \ s \ = \ 8 \ minutes \ et \ 52 \ s $

5.

Après une attente de 9 minutes, il restera 5% des noyaux radioactifs. L'attente suggérée de 8 à 9 minutes est cohérente avec cette valeur calculée.

Exercice n°36 P 130 : Quel âge ?

1.

Conservation du nombre de masse et de la charge.

$^{36}_{17} Cl \longrightarrow \ ^{36}_{18} Ar \ + \ ^{0}_{-1} e $

L'émission de la particule $^{0}_{-1} e $ permet d'identifier une radioactivité de type $\beta ^{ \ -}$

2.

CLa demi-vie du chlore 36, $t_{1/2} \ = \ 3,01.10^{ \ 5} \ ans$ est du même ordre de grandeur que l'âge présumé.

3.

La demi-vie du chlore 36, $t_{1/2} \ = \ \dfrac{ln2}{\lambda}$. La constante de temps $\lambda$ est donc l'inverse d'un temps, exprimé en $s^{ \ -1}$

4.

AN : $\lambda \ = \ \dfrac{ln2}{t_{1/2}} \ = \ \dfrac{ln2}{3,05.10^{ \ 5} \times 365,25 \times 365,25} \ = \ 7,3.10^{ \ -14} \ s^{ \ -1}$.

5.

$N(t) \ = \ N_0.e^{- \lambda .t}$.

6.

On cherche à déterminer l'instant $t$ pour lequel $N(t) \ = \ 0,38 \times N_0$.

$\Leftrightarrow \ N_0 \times e^{- \lambda .t} \ = \ 0,38 \times N_0$

$\Leftrightarrow \ e^{- \lambda .t} \ = \ 0,38$

$\Leftrightarrow \ \lambda .t \ = \ ln \left ( \dfrac{100}{38} \right )$

$\Leftrightarrow \ t \ = \ \dfrac{1}{\lambda} \times ln \left ( \dfrac{100}{38} \right )$

$\Leftrightarrow \ t \ = \ \dfrac{1}{7,3.10^{ \ -14}} \times ln \left ( \dfrac{100}{38} \right ) \ = \ 1,33.10^{ \ 13} \ s$

Soit : $420.000 \ ans$.