Avancement Chimique

Exercices

Exercice n°17 : Difluor.

1. $F_{2(g)} \ + \ Fe_{(s)} \ \longrightarrow \ 2 \ F_{(aq)}^{ \ -} \ + \ Fe_{(aq)}^{ \ 2+ }$

$n \left ( Fe \right ) = \dfrac{m_{Fe}}{M_{Fe}}= \dfrac{22,3}{55,8} = 0,40 \ mol$

$n \left ( F_2 \right ) = \dfrac{V_{F_2}}{V_{m}}= \dfrac{6}{24} = 0,25 \ mol$

2.

$ \begin{array}{ c |c |c |c |c } F_{2(g)} \ & + \ Fe_{(s)} \ & \longrightarrow \ & 2 \ F_{(aq)}^{ \ -} \ & + \ Fe_{(aq)}^{ \ 2+ }\\ \hline n \left ( F_2 \right ) & n \left ( Fe \right ) & & 0 & 0 \\ n \left ( F_2 \right ) - x & n \left ( Fe \right ) -x & & 2x & x \\ n \left ( F_2 \right ) - x_f & n \left ( Fe \right ) -x_f & & 2x_f & x_f \\ \end{array} $

La réaction s'arrête quand l'un des réactifs aura totalement disparu.

$$ \left\{ \begin{array}{ll}         n \left ( F_2 \right ) - x_f \ = \ 0  \\ ou \\         n \left ( Fe \right ) - x_f \ = \ 0      \end{array} \right. \ \Leftrightarrow \ \left\{ \begin{array}{ll}         n \left ( F_2 \right ) \ = x_f \\ ou \\         n \left ( Fe \right ) \ = x_f     \end{array} \right. \ \Leftrightarrow \ \left\{ \begin{array}{ll}         x_f \ = \ 0,25 \ mol \\ ou \\         x_f \ = \ 0,4\ mol     \end{array} \right. $$

 L'avancement final a donc pour valeur $x_f=0,25 \ mol$ quand il ne reste plus de difluor.

3. Le difluor$F_{2(g)}$ est le réactif limitant.

4. A l'état final : 

Il ne reste plus de difluor (réactif limitant) : $n_{final} \left ( F_{2(g)} \right ) = 0 \ mol$

Il reste : $n_{final} \left ( Fe \right ) = n \left ( Fe_{(s)} \right ) - x_f =0,40-0,25 = 0,15 \ mol$

Il est apparu :

$n_{final} \left ( F^{ \ -}_{(aq)} \right )= 2x_f = 2 \times 0,25 = 0,50 \ mol$

$n_{final} \left ( Fe^{ \ 2+}_{(aq)} \right )= x_f = 0,25 \ mol$

Exercice n°18 : Réaction entre les ions iodure et l'eau oxygénée .

$2\ I_{(aq)}^{ \ -}  \ + \ H_2O_{2(aq)} \ \longrightarrow \  I_{2(aq)} \ + \ 2 \ HO_{(aq)}^{ \ - }$

1. $n \left (I^{ \ -}  \right ) \ = \ c \ \times V = \ 1,0 \times 20.10^{ \ -3} = \ 20.10^{ \ -3} \ mol$

$n \left (H_2O_2  \right ) \ = \ \dfrac{C_m \times V}{M} \ = \ \dfrac{15 \times 20.10^{ \ -3}}{ 2 \times 1,0 + 2\times 16} = 8,82.10^{ \ -3} \ mol$

2. 

\begin{array}{ c |c |c |c |c }
  2 \ I^{ \ -}_{(aq)} \ & +  \ H_2O_{2(aq)} \ & \longrightarrow  \ & 2 \ I_{2(aq)} \ &  + \ 2 \ HO^{ \ - }_{(aq)}\\
 \hline
   n \left ( I^{ \ - } \right ) & n \left ( H_2O_2 \right ) & & 0 & 0 \\
  n \left ( I^{ \ - } \right ) - 2x & n \left ( H_2O_2 \right ) -x & & x & 2x \\
   n \left ( I^{ \ - } \right ) - 2x_f & n \left ( H_2O_2 ) \right ) -x_f & & x_f & 2x_f \\
\end{array}

3. La réaction s'arrêtera quand un des réactifs aura totalement disparu.

 L'avancement final a donc pour valeur $x_f=10.10^{ \ -3} \ mol$ quand il ne reste plus d'eau oxygénée.

4. A l'état final : 

Il ne reste plus d'eau oxygéné (réactif limitant) : $n_{final} \left ( H_2O_2 \right ) = 0 \ mol$

Il reste : $n_{final} \left ( I^{ \ -} \right ) = n \left ( I^{ \ -}  \right ) - 2x_f =20.10^{ \ -3 } - 2 \times 8,82.10^{ \ -3} = 2,36.10^{ \ -3} \ mol$

Il est apparu :

$n_{final} \left ( I_{2(aq)} \right )= x_f =  8,82.10^{ \ -3} \ mol$

$n_{final} \left ( HO^{ \ -}_{(aq)} \right )= 2x_f = 17,64.10^{ \ -3} \ mol$

Exercice n°19 : Réaction totale ou non totale.

$\ Ag_{(aq)}^{ \ +}  \ + \ Fe^{ \ 2+}_{(aq)} \ \longrightarrow \  Ag_{(s)} \ +  \ Fe_{(aq)}^{ \ 3+ }$

1. $n \left (Ag^{ \ +}  \right ) \ = \ c \ \times V = \ 0,1 \times 40.10^{ \ -3} = \ 40.10^{ \ -4} \ mol$

$n \left (Fe^{ \ 2+}  \right ) \ = \ c' \ \times V' = \ 0,2 \times 20.10^{ \ -3} = \ 40.10^{ \ -4} \ mol$

Les réactifs réagissant mole à mole, ils ont été introduits dans les conditions stoechimoétriques.

2. La couleur rouge (tube A) met en évidence les ions $Fe^{ \ 3+} $ dans le filtrat.

La couleur bleue (tube B) met en évidence les ions $Fe^{ \ 2+}$  dans le filtrat.

Le précipité blanc (tube C) met en évidence les ions $Ag^{ \ +}$  dans le filtrat.

3. Chauffer le mélange réactionnel permet d'accélérer la réaction chimique.

4. La présence des espèces réagissants $Fe^{ \ 2+}$ et $Ag^{ \ +}$ montre qu'elles sont encore présentes et que la réaction n'est pas terminée.

Exercice n°22 : Titrage d'un solution d'acide méthanoïque.

$\ I_{2(aq)}  \ + \ H_2CO_{2(aq)} \ \longrightarrow \  2 \ I_{2(aq)} \ +  \ CO_{2(g)} \ + 2 \ H^{ \ +}_{(aq)}$

1. Les 20 mL de la solution titrée ont été prélevés à l'aide d'une pipette jaugée équipée d'une poire aspirante. Ce prélèvement doit être effectué précisément.

2. Schéma du montage.

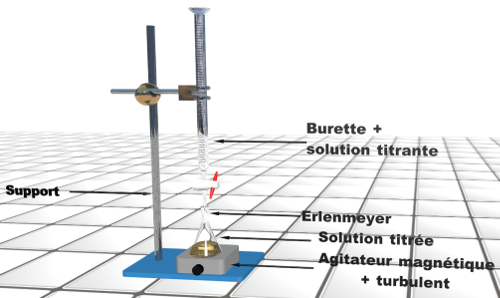
3. A l'équivalence, le diiode a totalement disparu, ainsi que la couleur jaune orangé.

4. Tableau d'avancement.

\begin{array}{ c |c |c |c |c | c}
   I_{(2aq)} \ & +  \ H_2CO_{2(aq)} \ & \longrightarrow  \ & 2 \ I^{ \ -}_{(aq)} \ &  + \  CO_{2(aq)} & \ 2 H^{ \ +}_{(aq)} \\
 \hline
   n \left ( I_{2(aq)} \right ) & n \left ( H_2O_2 \right ) & & 0 & 0 & 0\\
  n \left ( I_{2(aq)}  \right ) - x & n \left ( H_2O_2 \right ) -x & & 2x & x & 2x\\
   n \left ( I_{2(aq)}  \right ) - x_{éq} & n \left ( H_2O_2 ) \right ) -x_{éq} & & 2x_{éq}& x_{éq} & 2x_{éq}\\
\end{array}

5. A l'équilibre, les réactifs sont dans les proportions stoechiométriques : 

$ \dfrac {n \left ( I_{2(aq)} \right )}{1} = \dfrac{n \left ( H_2CO_{2(aq)} \right )}{1}$

6.  

soit : $ \dfrac{c_1  \times V_1}{1} \ = \ \dfrac{c_2 \times V_{éq}}{1}$

donc : $c_1 \ = \ \dfrac{c_2 \times V_{éq}}{V_1} \ = \ \dfrac{8,0.10^{ \ -2} \times 15,8.10^ { \ -3}}{20,0.10^{ \ -3}} = \ 6,32.10^{ \ -2} \ mol.L^{ \ -2}$

Exercice n°23 : Ions permanganate.

$2 \ MnO_{4(aq)}^{ \ -} \ + \ 5 \ H_2C_2O_{4(aq)} \ + \ 6 \ H^{ \ + }_{(aq)} \longrightarrow \ 2 \ Mn^{ \ 2+}_{(aq)} \ + \ 10 \ CO_{2(g)} \ + \ 8 \ H_2O_{(l)}$

1. A l'équivalence, les réactis sont dans les conditions stoechiométriques.

Ici : $ \dfrac{n \left ( MnO_4^{ \ -} \right )}{2} = \dfrac{n \left ( H_2CO_4 \right )}{5}$

2. L'équivalence, sera repérée quand tout le permanganate sera consommé. Etant l'espèce qui colore la solution, celle-ci aura perdu sa couleur.

3. Tableau d'avancement :

\begin{array}{ c |c |c |c |c | c | c}
   2 \ MnO_{4(aq)}^{ \ -} \ & +  \ 5 \  H_2C_2O_{4(aq)} & + \ 6 \ H^{ \ +}_{(aq)} \ & \longrightarrow  \ & 2 \ Mn^{ \ 2+}_{(aq)} \ &  + \ 10 \  CO_{2(g)} & \ 8 H_2O^{(l)} \\
 \hline
   n \left ( MnO_{4(aq)} \right ) & n \left ( H_2C_2O_4 \right ) & n \left ( H^{ \ +} \right ) & & 0 & 0 & solvant\\
  n \left ( MnO_{4(aq)}  \right ) - 2 \ x & n \left ( H_2C_2O_4  \right ) - 5 \ x & n \left ( H^{ \ +} \right ) - 6x  & & 2 \ x & 10 \ x &  solvant\\
   n \left ( MnO_{4(aq)} \right ) - 2 \ x_{éq} & n \left ( H_2C_2O_4  ) \right ) - 5 \ x_{éq}& n \left ( H^{ \ +} \right ) - 6 \ x_{éq}  &  & 2 \ x_{éq}& 10 \ x_{éq}  & solvant\\
\end{array}

A l'équivalence :

$ \dfrac{n \left ( MnO_4^{ \ -} \right )}{2} = \dfrac{n \left ( H_2CO_4 \right )}{5}$

Soit : $ c \ = \ \dfrac{c' \times V_{éq}}{V} = \dfrac{ 5,0.10^{ \ -2} \times 19,8}{10} \ = \ 9,9.10^{ \ -2} \ mol.L^{ \ -1}$

Exercice n°26 : Quel est le réactif limitant ?

1.

$ Cr_2O_{7(aq)}^{ \ 2-} \ + \ 3 \  Zn_{(s)} \ + \ 14 \ H^{ \ + }_{(aq)} \longrightarrow \  2 \ Cr^{ \ 3+}_{(aq)} \ + \  3 \ Zn^{ \ 2+}_{(s)} \ + \ 7 \ H_2O_{(l)}$

2.

\begin{array}{ c |c |c |c |c | c | c} Cr_2O_{7(aq)}^{ \ 2-} \ & + \ 3 \  Zn_{(s)} \ & + \ 14 \ H^{ \ +}_{(aq)} \ & \longrightarrow \ & 2 \ Cr^{ \ 3+}_{(aq)} \ & + \ 3 \ Zn^{ \ 2+}_{(s)} & \ 7 \ H_2O_{(l)} \\ \hline n \left ( Cr_2O_{7(aq)} \right ) & n \left ( Zn \right ) & n \left ( H^{ \ +} \right ) & & 0 & 0 & solvant\\ n \left ( Cr_2O_{7(aq)} \right ) - x & n \left ( Zn \right ) - 3 \ x & n \left ( H^{ \ +} \right ) - 14x & & 2 \ x & 3 \ x & solvant\\ n \left ( Cr_2O_{7(aq)} \right ) - x_{éq} & n \left ( Zn \right ) - 3 \ x_{éq}& n \left ( H^{ \ +} \right ) - 14 \ x_{éq} & & 2 \ x_{éq}& 3 \ x_{éq} & solvant\\ \end{array}

Détermination du réactif limitant : un des deux réacifs a totalement disparu.

 L'avancement final a donc pour valeur $x_f=1,0.10^{ \ -4} \ mol$ quand il ne reste plus de dichromate.

A l'état final : 

Il ne reste plus de dichromate (réactif limitant) : $n_{final} \left ( Cr_2O_7 \right ) = 0 \ mol$

Il reste : $n_{final} \left ( Zn \right ) = n \left ( zn  \right ) - 3x_f = \dfrac {20.10^{ \ -3 }}{65,4} - 3 \times 1,0.10^{ \ -4} = 5,8.10^{ \ -6} \ mol$

Il est apparu :

$n_{final} \left ( Cr^{ \ 3+} \right )= 2x_f =  2,0.10^{ \ -4} \ mol$

$n_{final} \left ( Zn^{ \ 2+}_{(aq)} \right )= 3x_f = 3,0.10^{ \ -4} \ mol$

Exercice n°28 : Concentration en ions thiosulfate d'une solution.

Réaction :

$ I_{2(aq)} \ + \ 2 \  S_2O_{3(aq)}^{ \ 2-}  \longrightarrow \  2 \ I^{ \ -}_{(aq)} \ + \  S_4O^{ \ 2-}_{6(aq)} \ + $

A léquivalence, les réactifs sont introduits dans les proportions stoechiométriques :

$ \dfrac {n \left ( I_{2} \right )}{1} =  \  \dfrac {n \left ( S_2O_3 \right )}{2}$

$\Leftrightarrow \ \dfrac {c_1}{20} \times V_{éq}{1} \ = \  \dfrac {c \times V}{2} $

$\Leftrightarrow \ \dfrac {8,0.10^{ \ -2 }}{20} \times  8 \ = \  \dfrac {c \times 10}{2} $

Soit : $c \ = \  \dfrac {2 \times 8,0.10^{ \ -2} \times 8}{20 \times 10} \ = \ 6,4.10^{ \ -3} \ mol.L^{ \ -1}  $

Exercice n°31 : Composition d'un statue.

1. 

$ \begin{array}{ c c c c c c c} & Sn & \ \overrightarrow{\longleftarrow} \ & \ Sn^{ \ 2+}_{(aq)} \ & + & 2 \ e^{ \ -} \\ 2 \ H^{ \ + }_{(aq)} & \ + \ 2 \ e^{ \ -} & \ \overrightarrow{\longleftarrow} \ & \ H_{ \ 2(g)}\\ \\ \hline \\ 2 \ H^{ \ + }_{(aq)} & \ + \ Sn & \ \longrightarrow \ & Sn^{ \ 2+}_{(aq)} & + & \ H_{ \ 2(g)} \end{array}$

2. On obtient une quantité : $n(H_2) \ = \ \dfrac{V}{V_m} \ = \ \dfrac{243.10^{ \ -3}}{24,0} \ = \ 1,0 \ mol$ de dihydrogène.

\begin{array}{ c |c |c |c |c |c |c |c}
   
   Réaction : &2 \ H^{ \ + }_{(aq)} & \ + \ Sn & \  \longrightarrow \ & Sn^{ \ 2+}_{(aq)} & +  \ H_{ \ 2(g)} \\
   \hline \\
   t_{initial} & excès & n & & 0 & 0 \\
   t & excès & n - x & & x & x \\
   t_{final} & excès & n - x_f & & x_f & x_f 
   
 \end{array}

L'acide introduit en excès, l'étain est le réactif limitant

L'avancement $x_f$ est donc : $x_f \ = \ 1,0 \ mol$

La quantité d'étain ayant réagi est donc la même, on en déduit une masse d'étain : $m(étain) = n \times M = 1,0 \times 118,7 \ = \ 118,7 \ g$.

Exercice n°33 : Eau oxygénée.

1. 

$
\begin{array} { c c c c c  }
H_2O_{2(aq)} & + 2 \ H^{ \ +}_{(aq)} & 2 \ e^{ \ -} \ & \overrightarrow{\longleftarrow} \ & \ 2 \ H_2O_{(l)} \\
O_{2(g)} \ & + \ 2 \ H^{ \ +} \ & + \ 2 \ e^{ \ -} \ & \overrightarrow{\longleftarrow} & \ H_2O_{2(aq)} \\
MnO_{4(aq)}^{ \ -} &  + 8 \ H^{ \ +}_{(aq)} & + 5 \ e^{ \ -} & \overrightarrow{\longleftarrow} & Mn^{ \ 2+}_{(aq)} & + 4 \ H_2O_{(l)}
 \end{array}
$

2. L'eau oxygénée est à la fois l'oxydant d'un couple et le réducteur d'un autre. 

3a,b. $MnO_{4(aq)}^{ \ -}$ étant l'oxydant du couple  $MnO_{4(aq)}^{ \ -} \ / \ Mn_{(aq)}^{ \ 2+}$, l'eau oxygénée $H_2O_{2(aq)}$ doit ici être considérée comme le réducteur.

$
\begin{array} { c c c c c c c c c}
 & & \ H_2O_{2(aq)} & \overrightarrow{\longleftarrow} & \ O_{2(g)} \ & \ 2 \ H^{ \ +} \ & + \ 2 \ e^{ \ -} & & \color{blue}{\times 5} \\
 \ MnO_{4(aq)}^{ \ -} & + \ 8 \ H^{ \ +}_{(aq)} & + 5 \ e^{ \ -} & \overrightarrow{\longleftarrow} & Mn^{ \ 2+}_{(aq)} & + \ 4 \ H_2O_{(l)} & & & \color{red}{\times 2}\\ 
 \hline 
 5 \ H_2O_{2(aq)} \ & + \ 2 \ MnO_{4(aq)}^{ \ -}\ & + \ 16 \ H^{ \ +}_{(aq)} \ & \longrightarrow & \ 5 \ O_{2(g)} & \ + \ 2 \ Mn^{ \ 2+}_{(aq)} & + \ 8 \ H_2O_{(l)} & \ + \ 10 \ H^{ \ +}_{(aq)} \\
 \end{array}
 $

En éliminant les ions $H^{ \ +}_{(aq)}$ en excédent, on arrive à :

$5 \ H_2O_{2(aq)} \ + \ 2 \ MnO_{4(aq)}^{ \ -}\ + \ 16 \ H^{ \ +}_{(aq)} \ \longrightarrow \ 5 \ O_{2(g)} \ + \ 2 \ Mn^{ \ 2+}_{(aq)} + \ 8 \ H_2O_{(l)} \ + \ 10 \ H^{ \ +}_{(aq)} $

3c.

$ \begin{array} { c | c | c | c | c | c | c | c } Réaction : & 5 \ H_2O_{2(aq)} \ & + \ 2 \ MnO_{4(aq)}^{ \ -}\ & + \ 6 \ H^{ \ +}_{(aq)} \ & \longrightarrow & \ 5 \ O_{2(g)} & \ + \ 2 \ Mn^{ \ 2+}_{(aq)} & + \ 8 \ H_2O_{(l)} & \ \\ \hline t_{initial} & n_{oxygénée} = \dfrac{c_m \times V}{M} & n_{Mn} = c' \times V_{éq} & excès & & 0 & 0 & solvant \\ t & \dfrac{c_m \times V}{M} - 5x & c' \times V_{éq} -2x & excès & & 5x & 2x & solvant \\ t_{final} & \dfrac{c_m \times V}{M} - 5x_{f} & c' \times V_{éq} -2x_{f} & excès & & 5x_{f} & 2x_{f}& solvant \\ \end{array} $

A l'équivalence, les réactifs sont introduits dans les conditions stoechiométriques :

$\dfrac {n(H_2O_2)}{5} \ = \  \dfrac {n(MnO_4)}{2}  \ \Leftrightarrow \ n(H_2O_2) \ = \ \dfrac {2 \times n(MnO_4)}{5} \ = \  \dfrac {2 \times c' \times V_{éq}}{5} \ =  \ \dfrac {2 \times 0,2 \times 17,6.10^{ \ -3}}{5} \ = \ 1,41.10^{ \ -3} \ mol$.

3d.

Cette quantité est celle dans les 10 mL de produit dosé. Dans 1 L, il y en a 100 fois plus : $N(H_2O_2) = 100 \times 1,41.10^{ \ -3} \ mol$

La concentration massique en $H_2O_2$ est donc : $c_m \ = 1,41.10^{ \ -3} \times 34 \ = \ 4,79 \ g.mol^{ \ -1} $.

Au lieu des $30 \ g.L^{ \ -1}$ attendus.

3e.

D'après la réaction fournie, il se libère moitié moins de dioxygène $O_{2(g)}$ que d'eau oxygénée $H_2O_{2(aq)}$.

On obtiendra donc une quantité de dioxygène $n(O_{2(g)} = \dfrac {1}{2} \times N(H_2O_2)$ soit un volume :

  $V(O_2) \ = \ \dfrac {1}{2} \times N(H_2O_2) \times V_m \ = \dfrac {1}{2} \times 1,41.10^{ \ -3} \times 22,4 \ = \ 1,58 \ L$.
 

Exercice n°35 : Titrage indirect de la vitamine C.

1. La quantité d'acide ascorbique dans un comprimé est : $n_{acide} \ = \ \dfrac {m}{M} \ = \ \dfrac {500.10^{ \ -3}}{176} \ = \ 2,84.10^{ \ -3} \ mol$.

Soit une concentration : $c \ = \ \dfrac{n}{V} \ = \ \dfrac{2,84.10^{ \ -3}}{250.10^{ \ -3}} \ = \ 1,14.10^{ \ -2} \ mol.L^{ \ -1} $

2. 

$ \begin{array} { c c c c c c c} & & \ I_{2(aq)} & \ + \ 2 \ e^{ \ -} & \overrightarrow{\longleftarrow} & \ 2 \ I^{ \ -}{(aq)} \ & & \\ & & & C_6H_8O_{6(aq)} & \overrightarrow{\longleftarrow} & C_6H_6O_{6(aq)} & + \ 2 \ H^{ \ +}_{(aq)} & + \ 2 \ e^{ \ -} \\ \hline & & \ I_{2(aq)} \ & + \ C_6H_8O_{6(aq)} \ & \overrightarrow{\longleftarrow} & \ 2 \ I^{ \ -}{(aq)} \ & \ + \ C_6H_6O_{6(aq)} & + \ 2 \ H^{ \ +}_{(aq)} \\ \end{array} $

3. La solution restant jaune, le diiode est toujours présent. Il est en excès.

4. 

$ \begin{array} { c | c | c | c | c | c | c | c} & Réaction & \ I_{2(aq)} \ & + \ C_6H_8O_{6(aq)} \ & \overrightarrow{\longleftarrow} & \ 2 \ I^{ \ -}{(aq)} \ & \ + \ C_6H_6O_{6(aq)} & + \ 2 \ H^{ \ +}_{(aq)} \\ \hline & t_{initial} & c \times V & n_{acide} \ - \ x & & 0 & 0 & \ 0 \\ & t & c \times V - x & n_{acide} \ - \ x & & 2 \ x & x & \ 2x \\ & t_{final} & c \times V - x_f & n_{acide} -x_f \  & & 2 \ x_f & x_f & \ 2x_f \\ \end{array} $

La quantité d'acide est : $n(acide) \ = \ 5,0.10^{ \ -3} \times 1,14.10^{ \ -2} \ = \ 5,68.10^{ \ -5} \ mol$.

La quantité de diiode introduite est : $n(I_2) \ = \ 5,00.10^{ \ -3} \times 20,0.10^{ \ -3} \ = \ 1,00.10^{ \ -4} \ mol$

Le diiode est bien excès, la solution reste jaune, il en reste $n_{final}(I_2) \ = \ 1,00.10^{ \ -4} \ - \ 5,68.10^{ \ -5} \ = \ 4,32.10^{ \ -5} \ mol$

5. 

$ \begin{array} { c c c c c c c} & & \ I_{2(aq)} & \ + \ 2 \ e^{ \ -} & \overrightarrow{\longleftarrow} & \ 2 \ I^{ \ -}{(aq)} \ & & \\ & & & 2 \ S_2O_{3(aq)}^{ \ 2-} & \overrightarrow{\longleftarrow} & S_4O_{6(aq)}^{ \ 2-} & + \ 2 \ e^{ \ -} & & \\ \hline & & \ I_{2(aq)} \ & + \ 2 \ S_2O_{3(aq)}^{ \ 2-} \ & \longrightarrow & \ 2 \ I^{ \ -}{(aq)} \ & \ + \ S_4O_{6(aq)}^{ \ 2-} & \\ \end{array} $

6.

$
\begin{array} { c | c | c | c | c | c | c | c}
& Réaction & \ I_{2(aq)}  \ & + 2 \ S_2O_{3(aq)}^{ \ 2-}  &   \overrightarrow{\longleftarrow} & \ 2 \ I^{ \ -}{(aq)} \ & \ + \ S_4O_{6(aq)}^{ \ 2-}  &   \\
\hline
& t_{initial} & n_{final}(I_2) & c_x  V &  & 0 & 0 &  \\
& t & n_{final}(I_2) \ - \ x &  c_x  V \ - \ 2 \ x &  & x & \ 2x \\
& t_{final} & n_{final}(I_2) \ - \ x_f & c_x  V_{éq} \ - \ 2 \ x_f &  & 2 \ x_f & x_f &  \\
 \end{array}
$

A l'équivalence, les réactifs sont dans les conditions stoechiométriques : $\dfrac{n(I_2)}{1} \ = \ \dfrac{n_{S_2O_3}}{2}$.

$n_{final}(I_2) \ - \ x_f  \ = \ \dfrac{c_x-2x_f}{2} \Leftrightarrow  \ c_x.V_e \ = \dfrac{2 \left ( n_f - x_f \right ) + 2x_f}{2}$

Soit : $c_x \ = \ \dfrac{2 n_{final}(I_2)}{V_e} = \ \dfrac { \ 2 \times 4,32.10^{ \ -5}}{15,0.10^{ \ -3}} \ = \ 5,76.10^{ \ -3} \ mol.L^{ \ -1}$

Exercice n°40 : Titrage de l'eau de javel.

1.La solution $S_1$ doit avoir un volume final $V_f=50 \ mL$. Cette solution est une solution diluée 10 fois de la solution mère. Il faut donc en prélever : $V_0 = \dfrac{V_f}{10} \ = \dfrac{50}{10} = 5 \ mL$.

2a.Pour prélever $10 \ mL$ de $S_1$, on utilise une pipette jaugée à 10 mL.

Pour prélever $20 \ mL$ de la solution contenant les ions iodure, on utilise une pipette jaugée à 20 mL.

2b.

$ \begin{array} { c c c c c c c} & & \ ClO_{(aq)}^{ \ -} & \ + \ 2 \ H^{ \ +}_{(aq)} & \ + \ 2 \ e^{ \ -} & \overrightarrow{\longleftarrow} & \ Cl^{ \ -}{(aq)} \ & \ + \ H_2O_{(l)} \ & \\ & & & & \ 2 \ I^{ \ -}_{(aq)} & \overrightarrow{\longleftarrow} & \ I_{2,(aq)} & + \ 2 \ e^{ \ -} \\ \hline & & \ ClO_{(aq)}^{ \ -} \ & + \ 2 \ I^{ \ -}_{(aq)} \ & + \ 2 \ H^{ \ +}_{(aq)} & \overrightarrow{\longleftarrow} & \ I_{2,(aq)} \ & \ + Cl^{ \ -}{(aq)} & + \ H_2O_{(l)} \\ \end{array} $

3a.

$ \begin{array} { c c c c c c c} & \ I_{2,(aq)} & + \ 2 \ e^{ \ -} & \overrightarrow{\longleftarrow} & \ 2 \ I^{ \ -}_{(aq)} \\ & & \ 2 \ S_2O^{ \ 2-}_{3,(aq)} \ & \overrightarrow{\longleftarrow} & \ S_4O^{ \ 2-}_{6,(aq)} & + \ 2 \ e^{ \ -} \\ \hline & \ I_{2,(aq)} & \ + \ 2 \ S_2O^{ \ 2-}_{3,(aq)} & \overrightarrow{\longleftarrow} & \ 2 \ I^{ \ -}_{(aq)} \ & \ + \ S_4O^{ \ 2-}_{6,(aq)} \\ \end{array} $

3b.La seule espèce colorée étant le diiode, une fois que tout celui-ci sera consommé, la solution deviendra incolore.

3c.On desse le tableau d'avancement de la réaction :

$$ \begin{array} { | c | c c c c c c |} \hline Réaction : & \ I_{2,(aq)} & \ + \ 2 \ S_2O^{ \ 2-}_{3,(aq)} & \longrightarrow \ 2 \ I^{ \ -}_{(aq)} \ & \ + \ S_4O^{ \ 2-}_{6,(aq)} \\ \hline x = 0: & n_2 & n_3 & & 0& 0\\ \hline x : & n_2 -x & n_3 - 2x & & 2x& x\\ \hline x_f : & n_2 -x_f & n_3 - 2x_f & & 2x_f & x_f \\ \hline \end{array}$$

A léquivalence, les réactifs sont dans les conditions stoechiométiques :$\dfrac{n_2}{1} \ = \dfrac{n_3}{2}$

La quantité de diiode ayant réagi a pour valeur : $n_2\ = \dfrac{n_3}{2} \ = \ \dfrac{0,1 \times 7,6.10^{ \ -3}}{2} \ = \ 3,8.10^{ \ -4} \ mol$

3d.Cette valeur correspond à la quantité d'ions $ClO^{ \ -}$ qui a réagi lors de la première réaction : $n_1 \ = \ 3,8.10^{ \ -4} \ mol$

3e.La concentration en ions hypochlorites dans la solution $S_1$ est donc $c_1 \ = \dfrac{n_1}{V} \ = \ \dfrac{3,8.10^{ \ -4}}{10.10^{ \ 3}} \ = \ 3,8.10^{ \ -2} \ mol.L^{ \ -1}$

La solution commerciale ayant été diluée 10 fois, sa concentration est : $c_0 \ = \ 10 \times c_1 \ = 3,8.10^{ \ -1} mol.L^{ \ -1}$

4.La réaction fournie dans le doc1. montre que l'on forme autant de dichlore $Cl_2$ qu'on a consommé d'hypochlorite $ClO^{ \ -}$, soit $n(Cl_2) \ = c_0 \times 1 \ = 3,8.10^{ \ -1} \times 1 \ = \ 3,8.10^{ \ -1} \ mol$

5.La masse volumique de l'eau de javel est $\rho \ = \ 1,03 \ g/mL \ = \ 1,03.10^{ \ 3} g/L$ : 1 L d'eau de javel a une masse $m \ = \ 1030 \ g$.

La masse de dichlore produite est : $m \left ( Cl_2 \right ) \ = \ n(Cl_2) \times M(Cl_2) \ = \ 3,8.10^{ \ -} \times \left ( 2 \times 35,5 \right )\ = \ 27,0 \ g$.

Soit un pourcentage de $100 \times \dfrac{27}{1030} \ = \ 2,6 \%$ de chlore actif.