Chap5_interaction

Exercice n°12 : La machine de Wimshurst.

1. Il s'agit d'une interaction électrostatique. Les sphères portant des charges opposées, cette interaction est attractive.

2. 

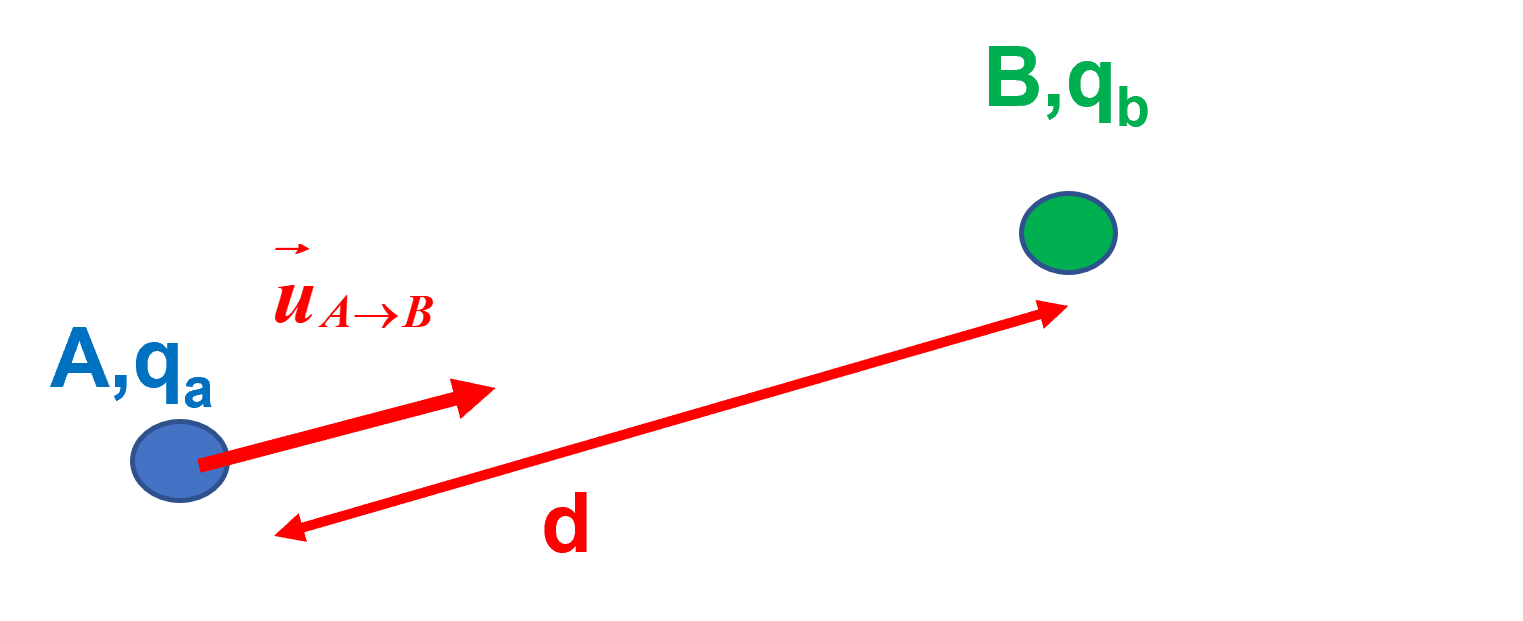
2. 

$\overrightarrow {F} _{A \rightarrow B}= - \overrightarrow {F}_{B \rightarrow A}= k \times \dfrac {q_A \times q_B}{d^2} \times \overrightarrow {u}_{A \rightarrow B}$

$F_E = 9,0.10^{ \ -9} \times \dfrac { \left | -10^{-6} \right | \times \left | 10^{-6} \right |}{ \left (5,0.10^{-2} \right ) ^{2}} = 3,6 \ N$

3. On suppose que les deux sphères ont une masse de 5,0 g. Calculer la valeur de la force gravitationnelle exercée l'une sur l'autre.

Expression de la force de gravitation :

$\overrightarrow {F} _{A \rightarrow B}= - \overrightarrow {F}_{B \rightarrow A}= -G \times \dfrac {m_A \times m_B}{d^2} \times \overrightarrow {u}_{A \rightarrow B}$

Calcul de sa valeur :
$F_G = 6,67.10^{ \ -11} \times \dfrac { \ 5,0.10^{-3} \times 5,0.10^{-3}}{ \left (5,0.10^{-2} \right ) ^{2}} = 6,67.10^{ \ -13} \ N$

4. Comparer ces deux forces.

Dans la situation présente, la force élcetrostatique est attractive, de même que la force de gravitation (qui l'est toujours).

Pour comparer les valeurs de ces forces, on effectue le rapport de deux grandeurs de même dimension : le résultat de ce rapport sera sans dimension.

$\dfrac {F_E}{F_G} = \dfrac {3,6}{6,67.10^{- \ 13}} = 5,4.10^{12} $

La force électrostatique est $10^{12} $ fois plus grande que la force gravitationnelle !!

Exercice n°13 : Attraction ou Répulsion ?

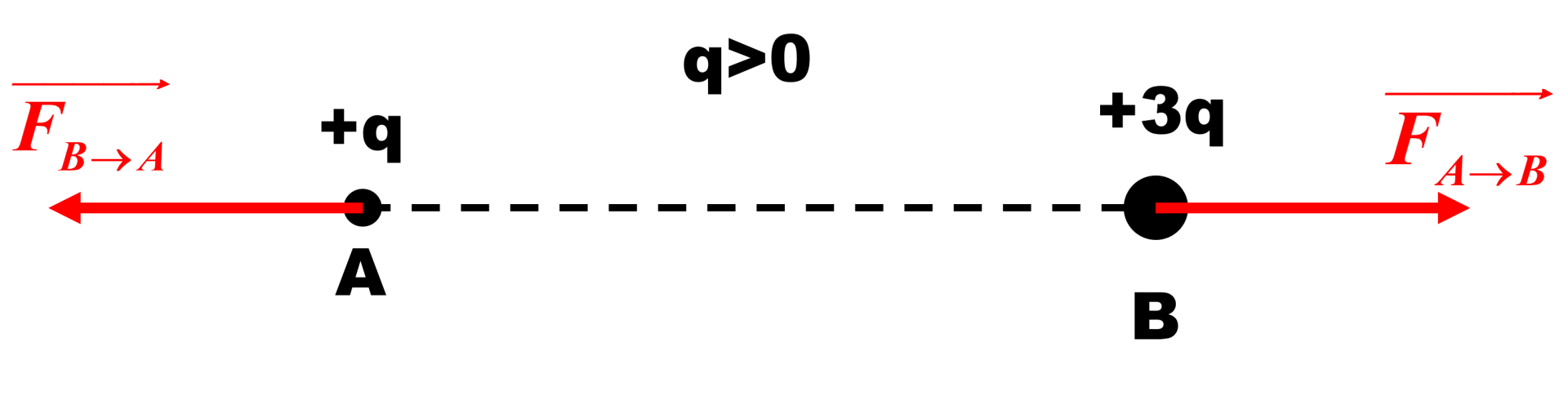
1. Les deux charges sont de même signe, les charges se repoussent.

2. $\overrightarrow {F} _{A \rightarrow B}= - \overrightarrow {F}_{B \rightarrow A}= k \times \dfrac {q \times 3q}{d^2} \times \overrightarrow {u}_{A \rightarrow B}= k \times \dfrac {3q^2}{d^2} \times \overrightarrow {u}_{A \rightarrow B}$

3. Voir ci-dessus.

4. Les deux charges sont de même signe, les charges se repoussent, la situation reste inchangée.

$\overrightarrow {F} _{A \rightarrow B}= - \overrightarrow {F}_{B \rightarrow A}= k \times \dfrac {-q \times \left ( -3q \right )}{d^2} \times \overrightarrow {u}_{A \rightarrow B}= k \times \dfrac {3q^2}{d^2} \times \overrightarrow {u}_{A \rightarrow B}$

Exercice n°14 : Analogie entre les deux forces.

1. L'interaction gravitationnelle est toujours attractive.

2. $\overrightarrow {F} _{A \rightarrow B}= - \overrightarrow {F}_{B \rightarrow A}= -G \times \dfrac {m_A \times m_B}{d^2} \times \overrightarrow {u}_{A \rightarrow B}$

3. 

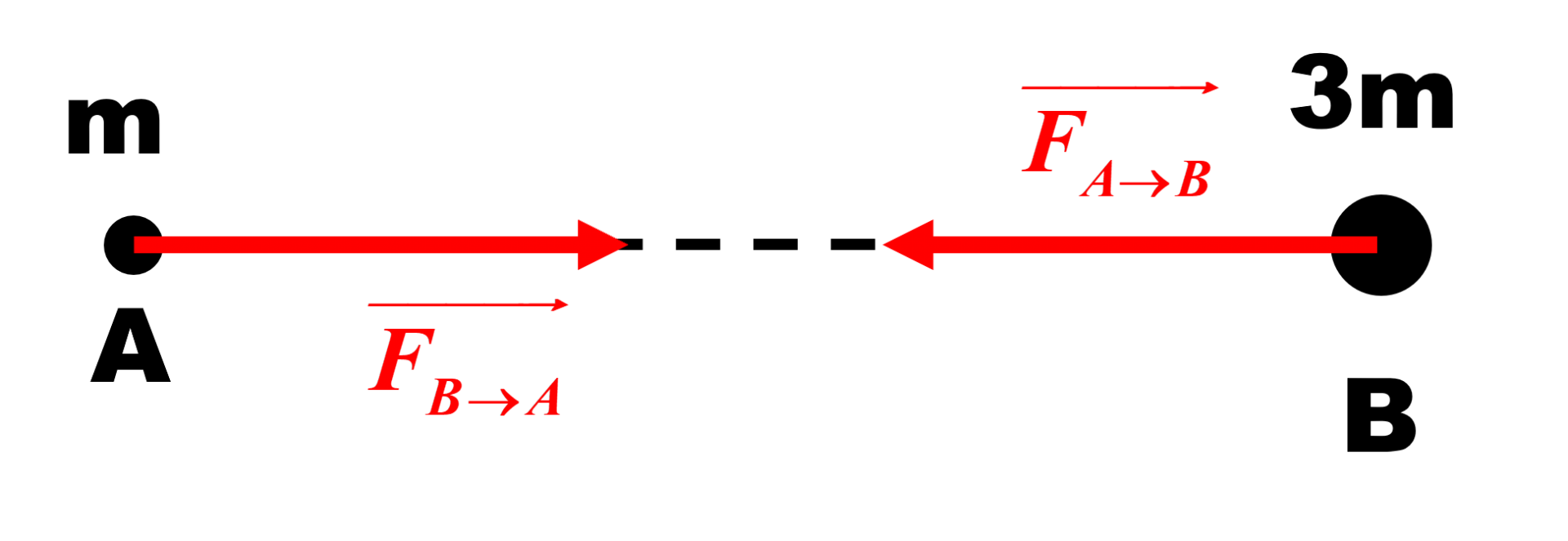4. Dans les deux cas, la forces est :

• inversement proportionnelle au carré de la distance entre les deux corps.

• dirigée selon le vecteur $ \overrightarrow {u}_{AB}.

Dans le cas de la force de gravitation, elle est prportionnelle au produit des masses.

Dans le cas de la force électrostatique, elle est proportionnelle au produit des charges.

Exercice n°15 : La Lune, satellite naturel de la Terre.

1. Car la Terre exerce une force de gravitation sur la Lune, et réciproquement. Elles tournent l’une autour de l’autre.

2a. $\overrightarrow {F} _{T \rightarrow L}= - \overrightarrow {F}_{L \rightarrow T}= -G \times \dfrac {m_L \times m_T}{d^2} \times \overrightarrow {u}_{T \rightarrow L}$

2b. $F=  6,67.10^{ \ -11 }\times \dfrac {7,35.10^{ \ 22} \times 5,98.10^{ \ 24}}{\left ( 3,84.10^{5} \times 10^{3} \right )^2} = 2,0.10^{20} \ N$

3a,b.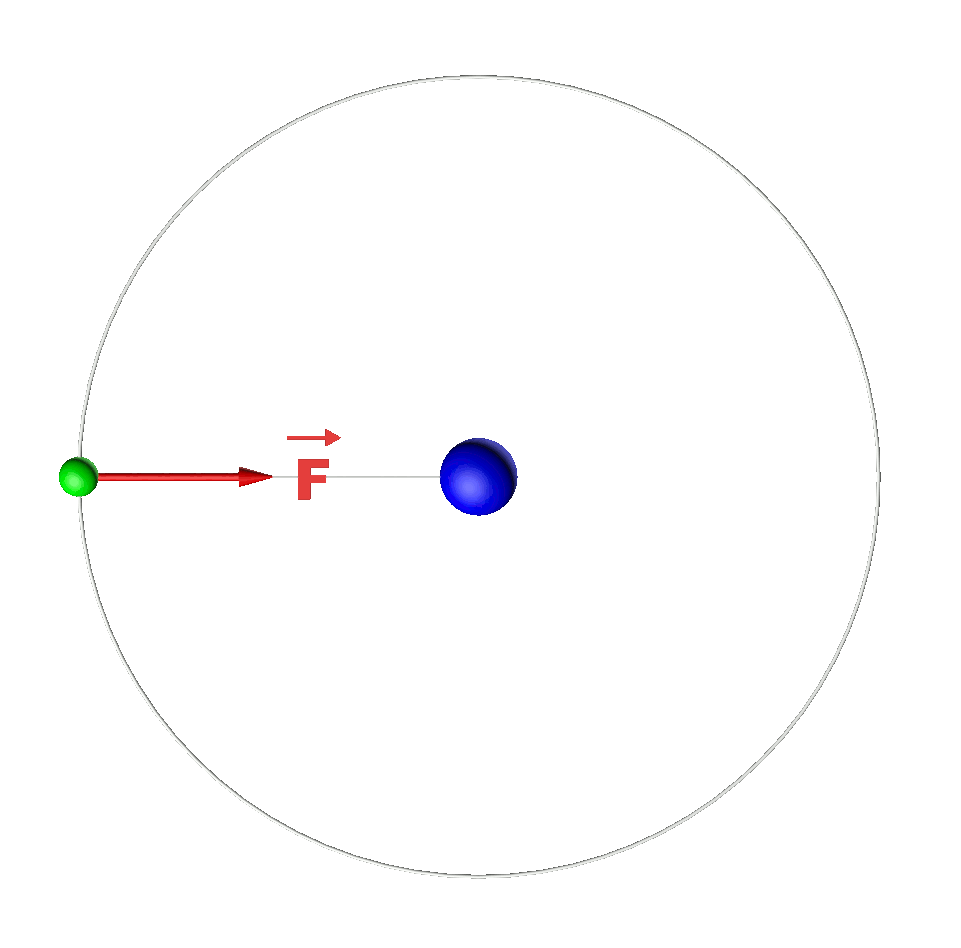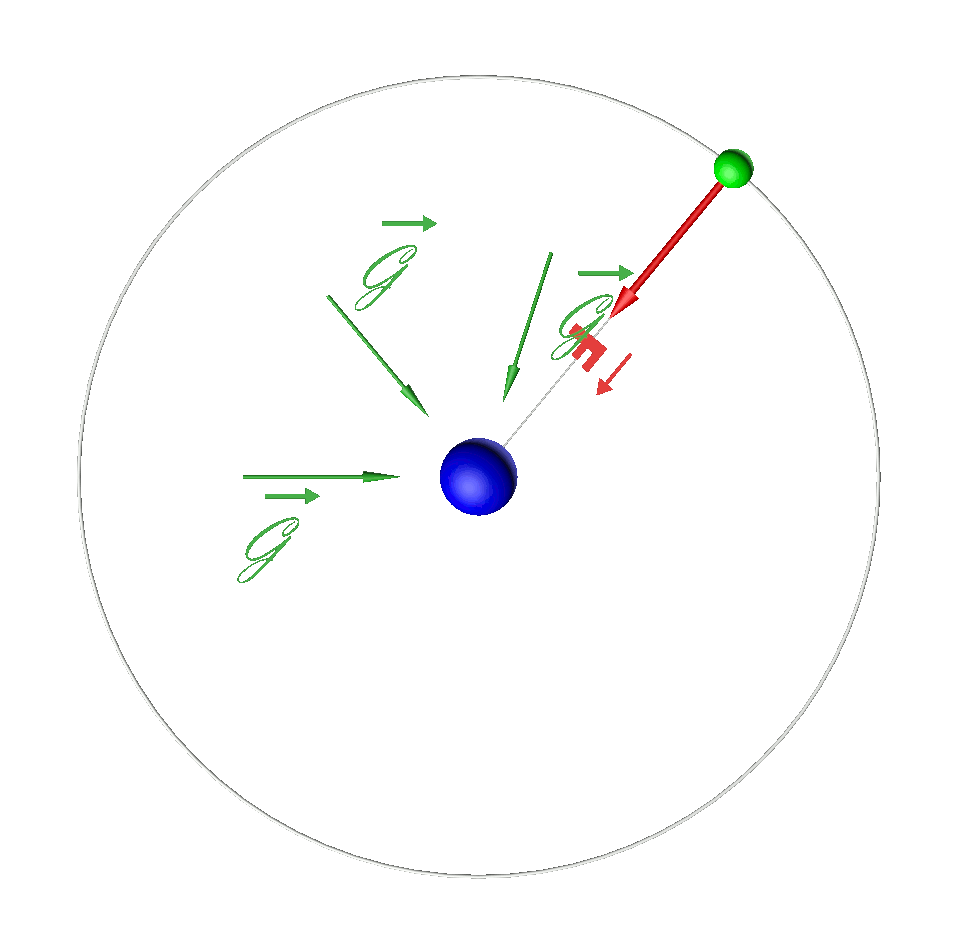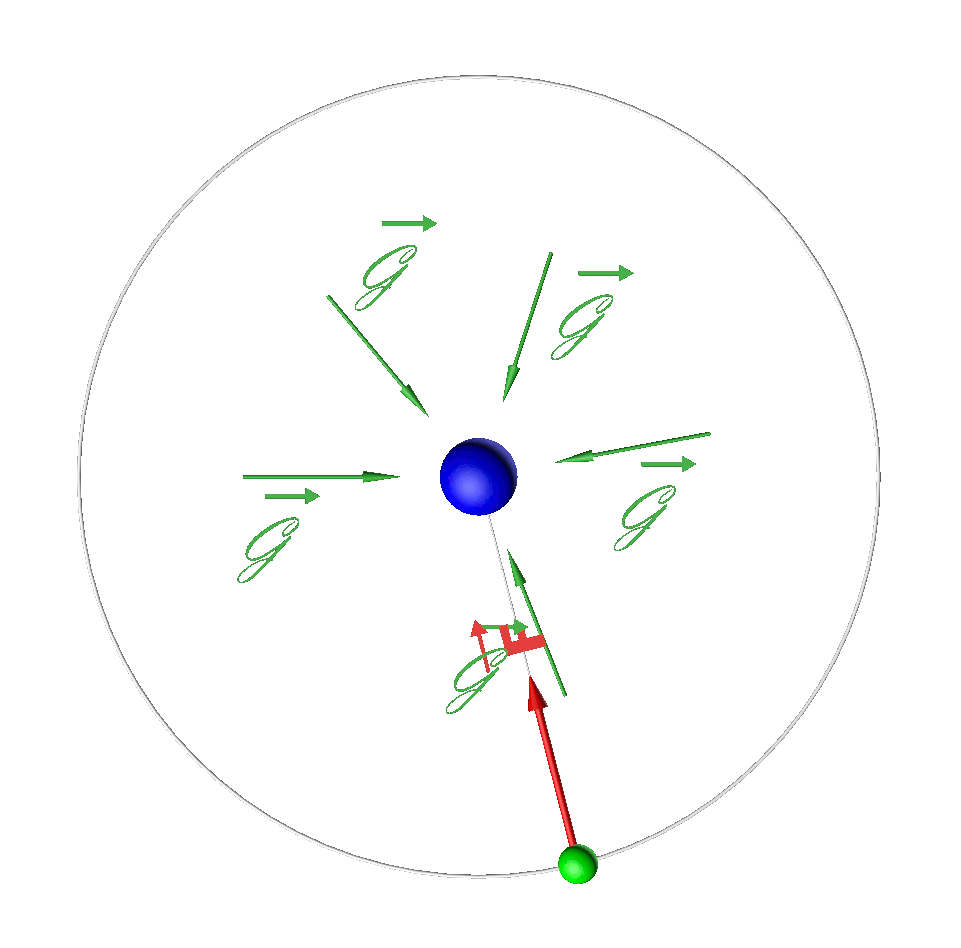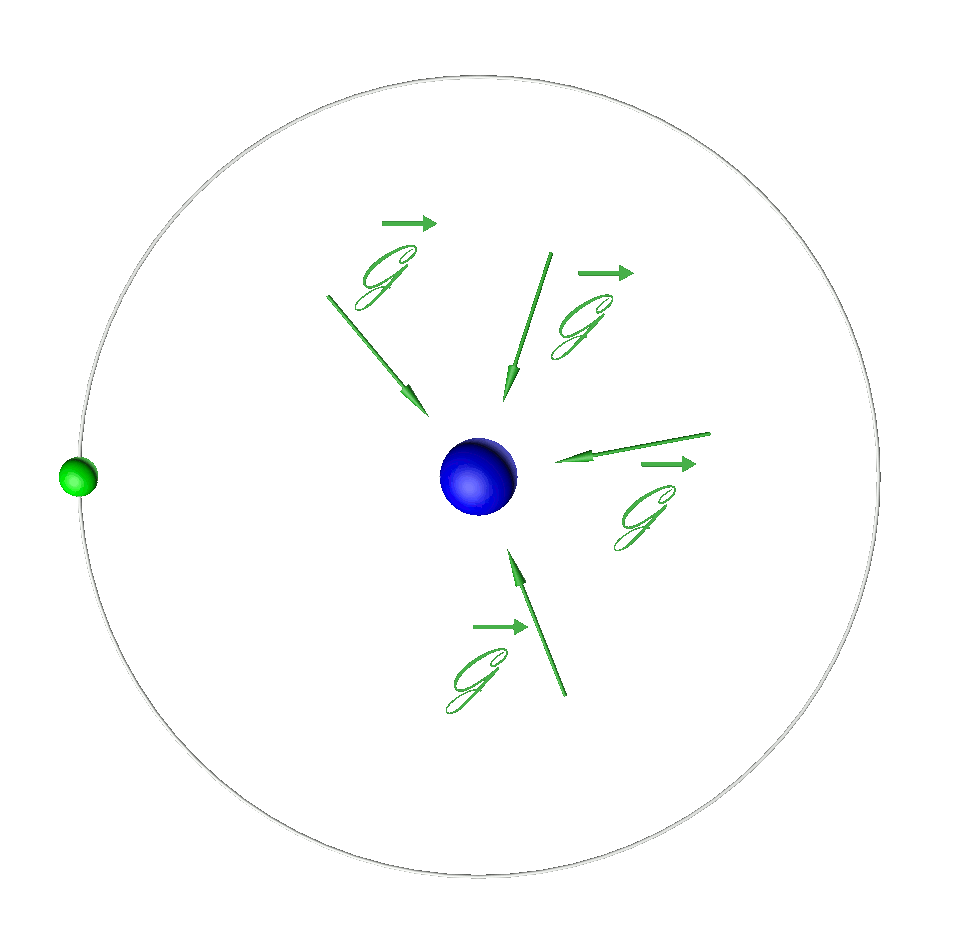 

Exercice n°18 : Deux masses et leurs lignes de champ.

1a. Car la Terre exerce une force de gravitation sur la Lune, et réciproquement. Elles tournent l’une autour de l’autre.

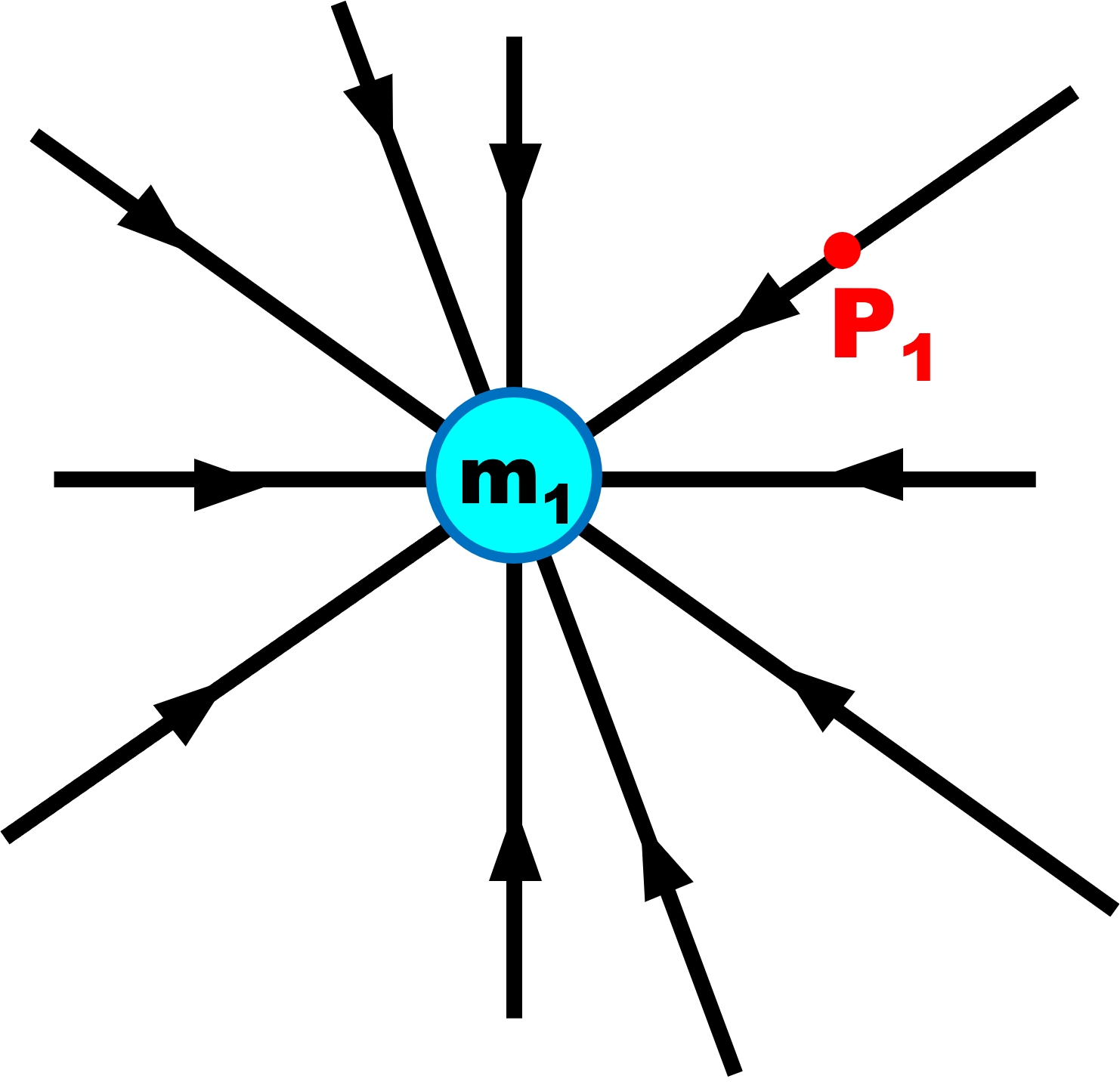
1b. Le champ de gravitation est dirigé du corps P₁ vers le centre de l'astre de masse m₁. 

2. Les lignes de champ engendrées par l'astre de masse m₁ sont différentes car le corps subit à la fois l'attraction des deux corps de masse m₁ et m₂.

3,4. 

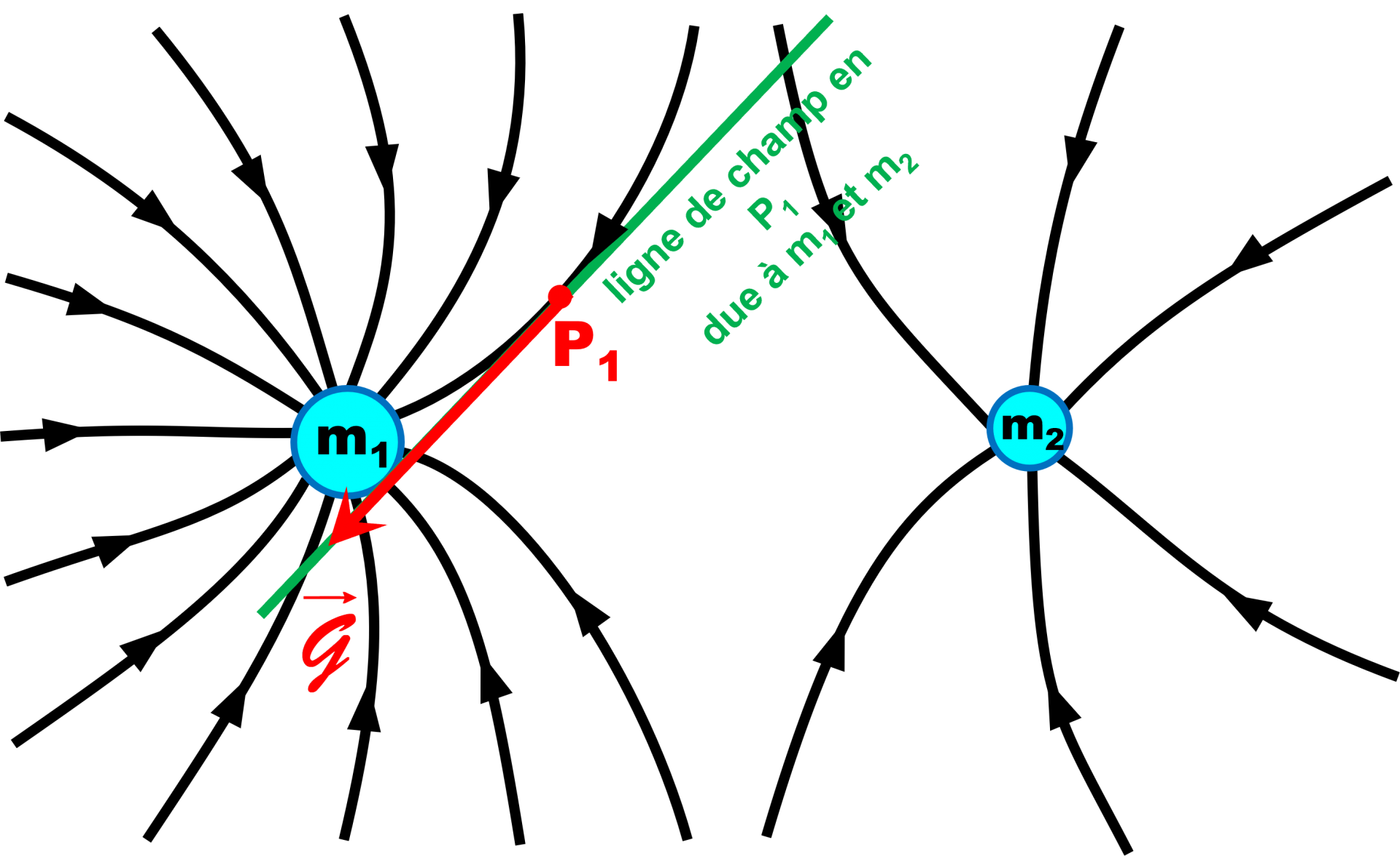5. Le champ en P₁ est tangent à la ligne de champ passant par P₁ .

Exercice n°20 : Vecteur champ électrostatique.

1. $\overrightarrow {E}= k \times \dfrac {q}{d^2}\overrightarrow {u}$

2. $E= 9,0 \times 10^9 \times \dfrac {9,6 \times 10^{-18}}{ \left (2,0 \times 10^{-2} \right ) ^2} = 2,16 \times 10 ^{ \ - 4} \ V.m^{ \ -1}$

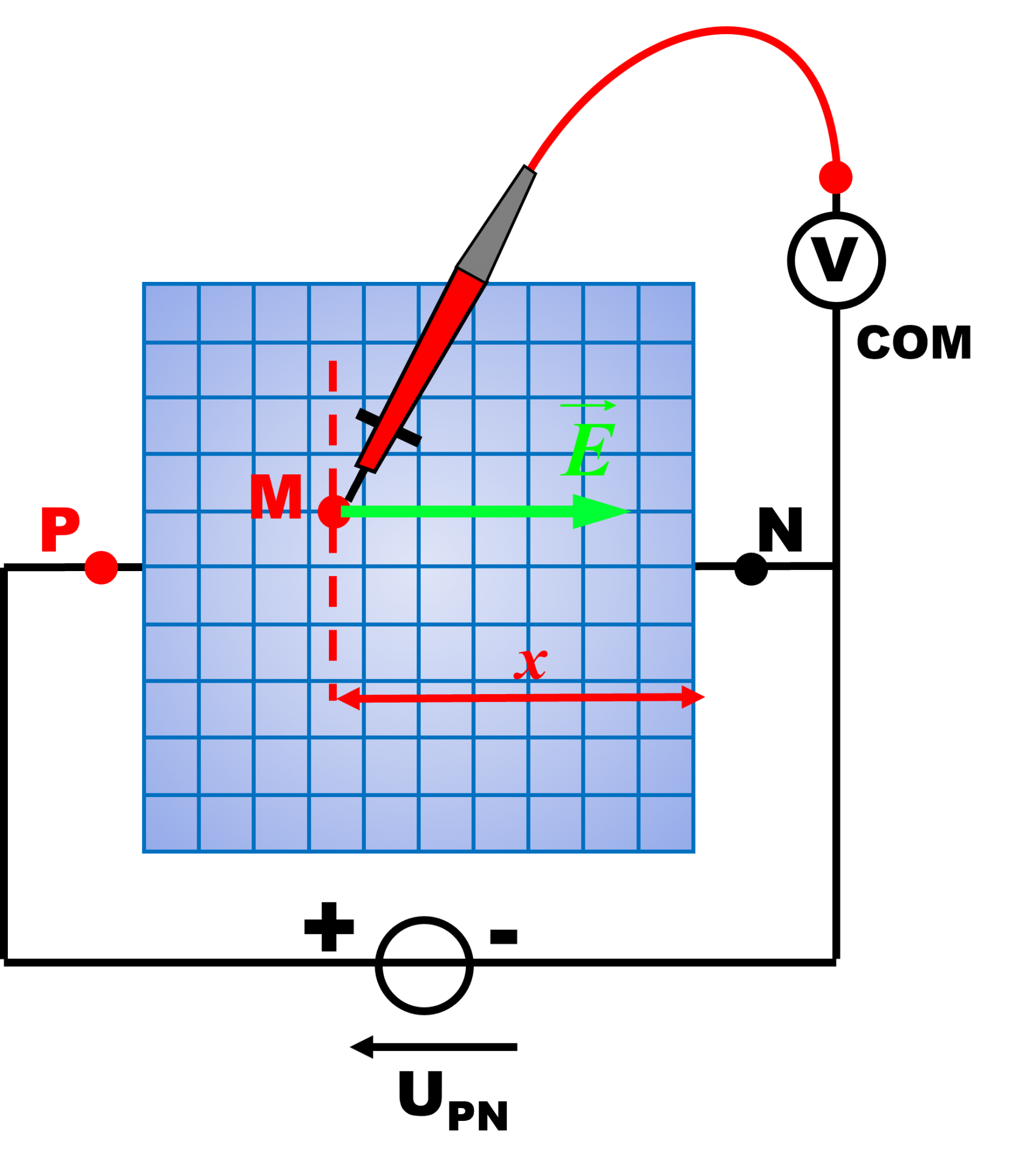
3. La borne "COM" du voltmètre est reliée au point M. Il s'agit donc de la borne négative. Le champ magnétique est donc dirigé du point M (chargé positivement) vers le point N.

Exercice n°23 : Vecteur champ.

1. La charge est négative, car le champ est dirigé vers la charge.

2. On mesure une distance $d = 4,6 \ cm$

3. On mesure $E = 2 \ V.m^{ \ -1}$ (2 cm papier)

4. $E= | k \times \dfrac{q}{d^2} |$ donc : $ |q | = | \dfrac{E \ times d^2}{k} | = \dfrac{2 \times \left ( 4,6.10^{ \ -2} \right )^{ \ 2}}{9,0.10^{ \ 9}} \ = 4,7.10^{ \ -13} \ C$

La valeur de la charge est donc $q = - 4,7.10^{ \ -13} \ C$

Exercice n°29 : Masse des astres.

1,2.Le champ engendré en $P$ par les masses situées en $M_1$ et $M_2$ est la somme des champs générés par ces deux masses : $\overrightarrow{\cal G} \ = \overrightarrow{\cal G_1} + \overrightarrow{\cal G_2}$

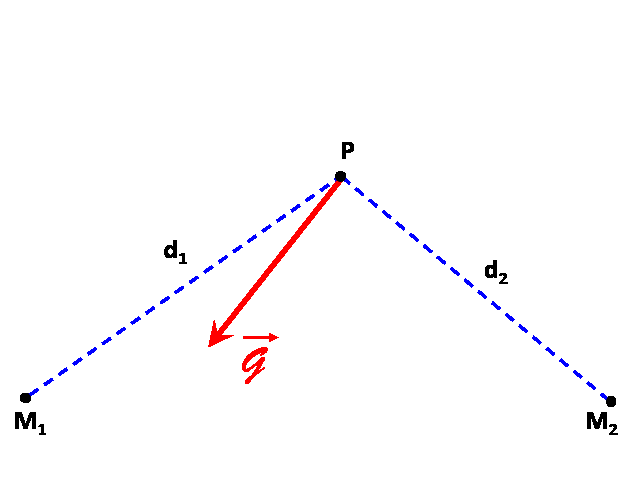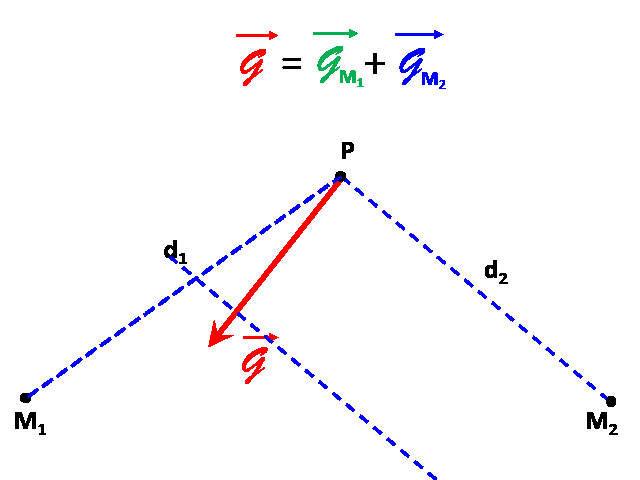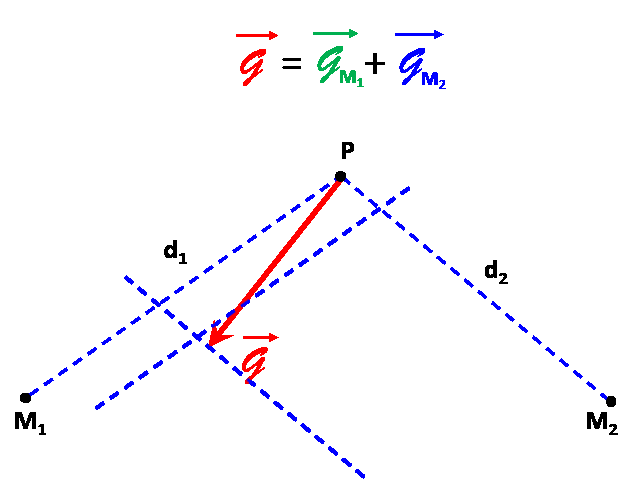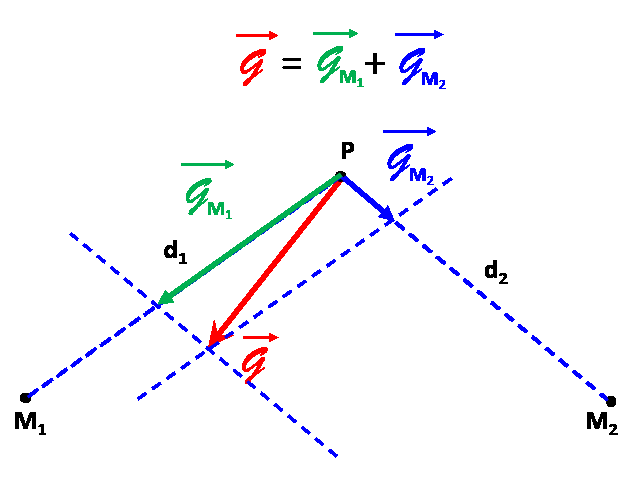
3.On mesure alors pour chaque vecteur tracé :

${\cal G_1} \ : \ 2,6 \ cm$ soit : ${\cal G_1} = 2,6 \times 1,0.10^{ \ -2} = 2,6.10^{ \ -2} N.kg^{ \ -1}$

${\cal G_2} \ : \ 0,8 \ cm$ soit : ${\cal G_1} = 0,8 \times 1,0.10^{ \ -2} = 8,0.10^{ \ -3} N.kg^{ \ -1}$

4.

On mesure pour $d_1 \ : \ 4,4 \ cm$ soit : $d_1 = 4,4 \times 10^{ \ 8} \ = 4,4.10^{ \ 8} \ m$

On mesure pour $d_1 \ : \ 4,1 \ cm$ soit : $d_1 = 4,1 \times 10^{ \ 8} \ = 4,1.10^{ \ 8} \ m$

L'expression du champ est : ${\cal G}=G \times \dfrac{m}{d^2}$

On en déduit : $m \ = \ \dfrac{{{\cal G}} \times d^2}{G}$

Donc : $m_1 \ = \ \dfrac{{{\cal G_1}} \times d_1^2}{G} \ = \dfrac{2,6.10^{ \ -2} \times \left (4,4.10^{ \ 8} \right )^2} {6,67.10^{ \ -11}} \ = \ 7,5.10^{ \ 25} \ kg $.

Et :$m_1 \ = \ \dfrac{{{\cal G_2}} \times d_2^2}{G} \ = \dfrac{8,0.10^{ \ -3} \times \left (4,1.10^{ \ 8} \right )^2} {6,67.10^{ \ -11}} \ = \ 2,0.10^{ \ 25} \ kg $.

Exercice n°34 : Déviation de particule dans un champ.

1,2,3a,3b.

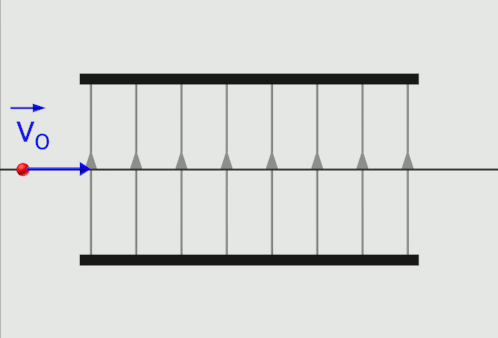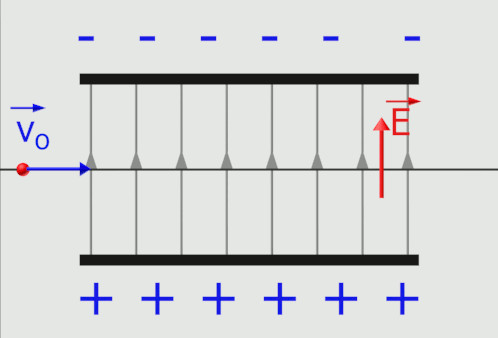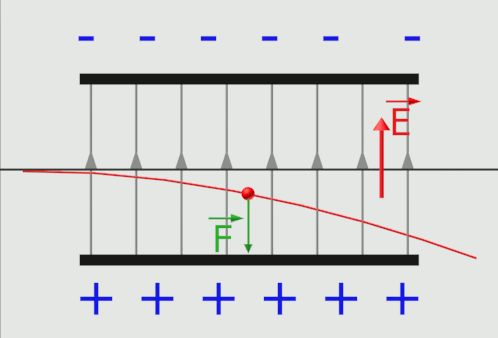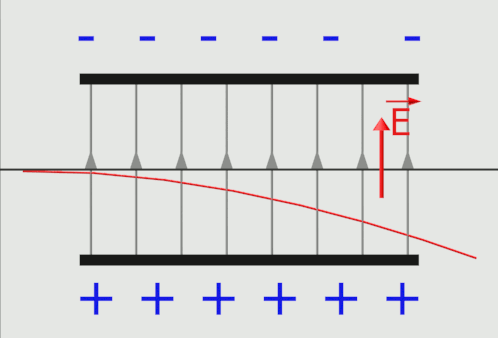Le vecteur champ électrostatique $\overrightarrow{E}$ est tangent aux lignes de champ, et dans le même sens. Les lignes de champ sont orientées des charges positives vers le charges négatives. L'électron pénétrant dans le champ subit la force $\overrightarrow F \ = -e \times \overrightarrow E$. Il sera dévié vers la plaque positive du condensateur.

3c.$F = 1,60.10^{ \ -19} \times 2,0.10^{ \ 3} = 3,2.10^{ \ -16} \ N$

3c.Pour un proton, de charge opposée à celle de l'électron, l'intensité de la force sera la même, mais la force sera dirigée vers la plaque chargée négativement. Il sera dévié vers cette plaque.