Cohésion de la matière
Exercice n°8 P 95 : Solide ionique ou moléculaire.
a. Le chlorure de sodium $NaCl_s$ est un solide ionique.
b. Le diiode $I_{2,s}$ est un solide moléculaire.
c. Le saccharose $C_{12}H_{22}O_{11}$ est un solide moléculaire.
d. La glace $H_2O_s$ est un solide moléculaire.
e. Le chlorure de lithium $LiCl_s$ est un solide ionique.
f. Le chlorure d'iode $LiCl_s$ est un solide moléculaire.
g. Le fluorure de sodium $LiCl_s$ est un solide ionique.
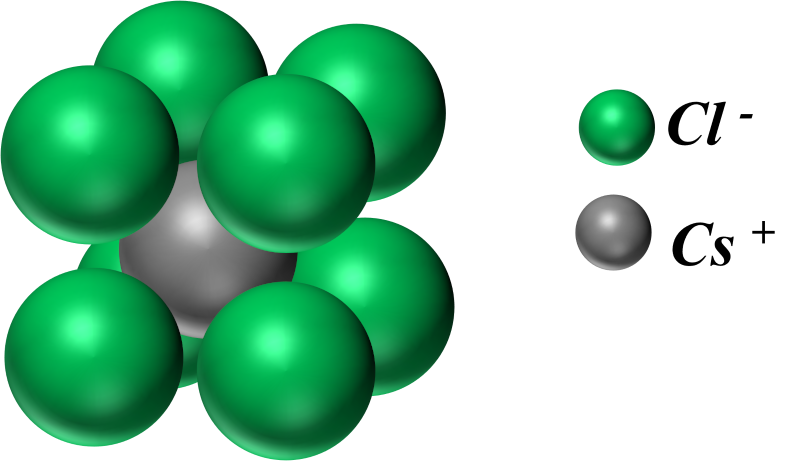
Exercice n°9 P 95 : Cohésion du chlorure de césium ?
 |
 |
1.
Constitué d'ions chlorure $Cl^{ \ -}$ et d'ions césium $Cs^{ \ +}, il s'agit d'un solide ionique.
2.
On observe des interactions électrostatiques répulsives entre les anions et entre les cations, et des interactions électrostatiques attractives entre les anions et les cations.
3a.
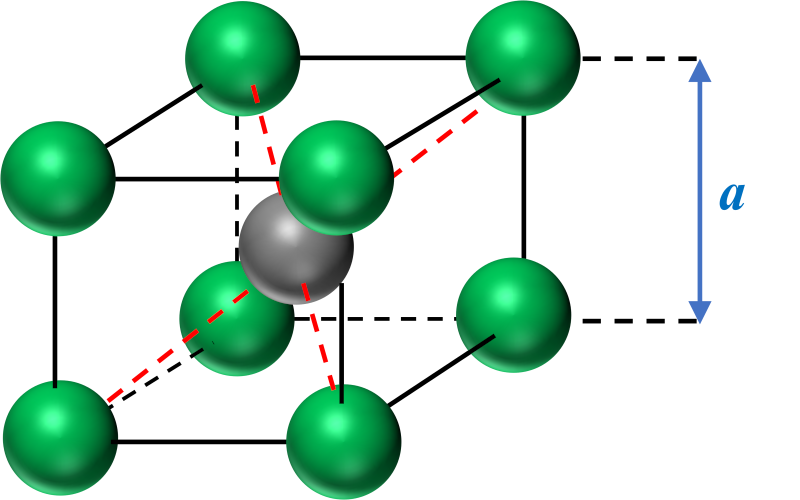
Les ions chlorures $Cl^{ \ - }$ sont distants de la longueur de l'arête : $d_{Cl/Cl} \ = \ a$.
3b.
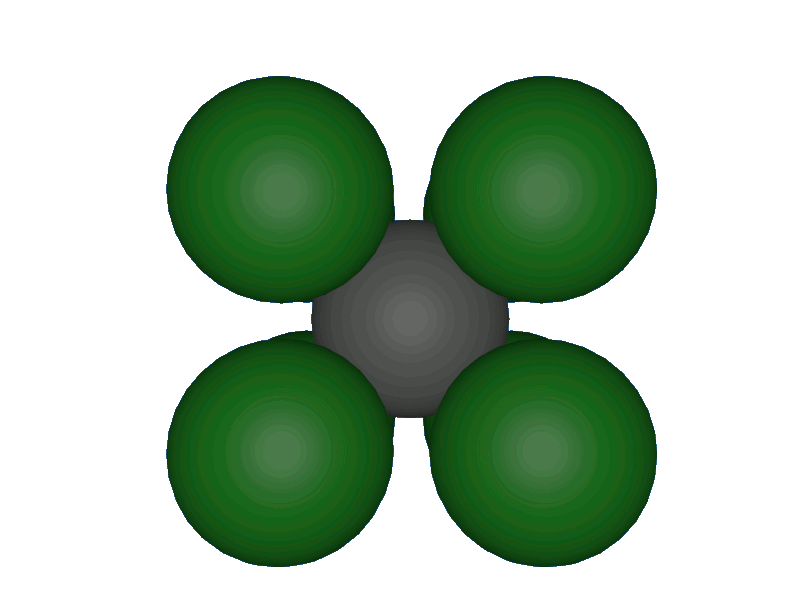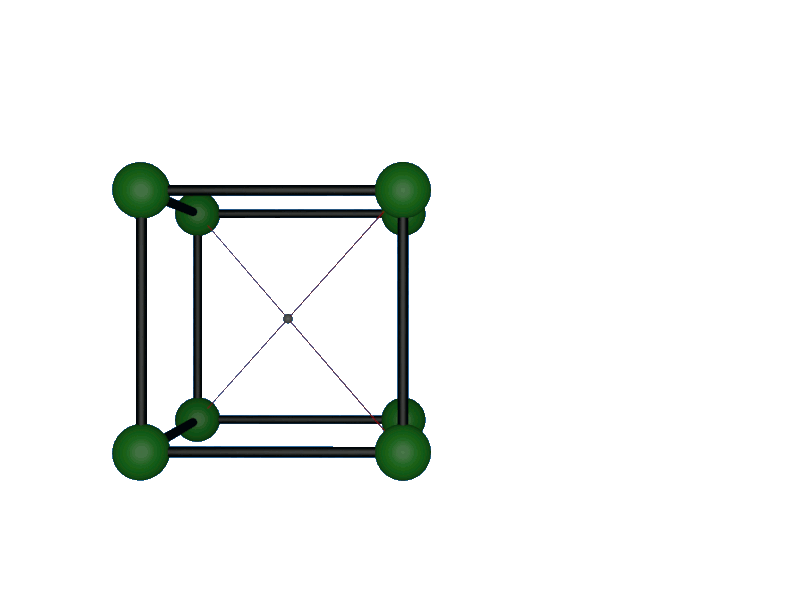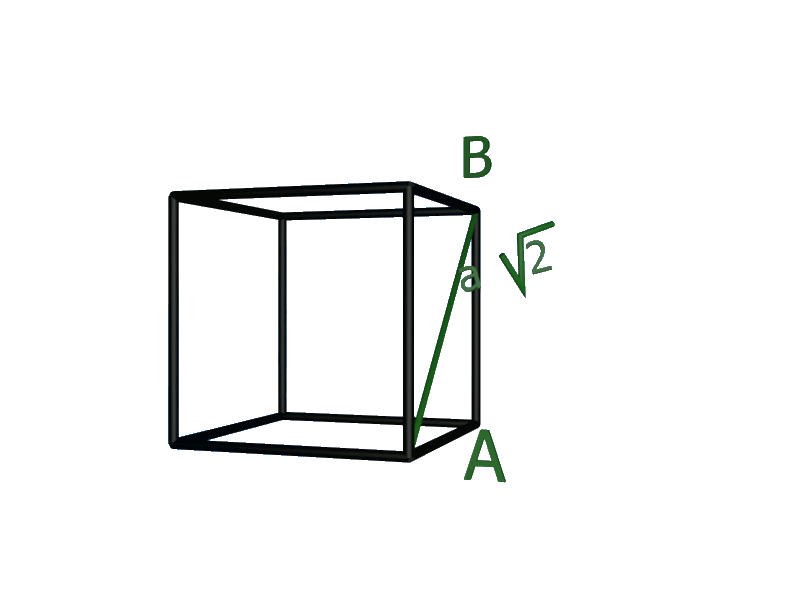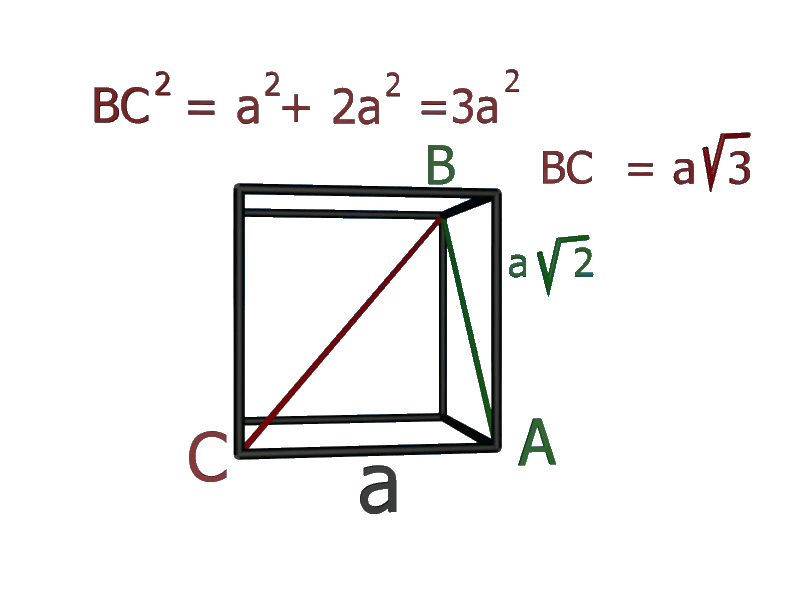
La distance séparant deeux ions $Cl^{ \ -}$ et $Cs^{ \ + }$ est donc égake à la moitié de la diagonale principale du cube : $d_{Cs/Cs} \ = \ \dfrac{a \times \sqrt{3}}{2}$.
3c.
Comparons la valeur de la force électrostatique de répulsion entre deux ions chlorures $Cl^{ \ - }$ et celle de la force d'attraction entre deux ions $Cl^{ \ -}$ et $Cs^{ \ +}$ en effectuant leur rapport.
$\dfrac{F_{Cl/Cl}}{F_{Cs/Cl}} = \ \dfrac{\dfrac{k \times e^{\ 2}}{a^{ \ 2}}}{ \dfrac{k \times e^{\ 2}}{3a^{ \ 2}/4}} \ = \ \dfrac{k \times e^{\ 2}}{a^{ \ 2}} \times \dfrac{3a^{ \ 2}}{4k \times e^{\ 2}} \ = \ 0,75$
4.
La force d'attraction anion/cation est donc plus importante que la force de répulsion anion/anion. Ce qui explique la cohésion du solide ionique.
Exercice n°11 P 95 : Avec ou sans hydrogène ?
1.
Au vu de la différence d'électronégativité entre les atomes constituant les molécules, elles sont polaires.
2.
Pour une température inférieure à la température de fucion, les composés sont solides.
3a.
Les molécules étant polaires, il existe des interactions attractives dues aux charges partielles.
Des ponts hydrogène peuvent se former entre les molécules d'eau, ce qui n'est pas le cas dans le sulfure d'hydrogène car le soufre est trop peu électronégatif.
Exercice no 13 P96 : Equations de dissolution dans l'eau.
a. $NaCl_{(s)} \ \xrightarrow{ \ \ \ \ eau \ \ \ \ } \ Na_{(aq)}^{ \ +} \ + \ Cl_{(aq)}^{ \ -}$
b. $CoCl_{2(s)} \ \xrightarrow{ \ \ \ \ eau \ \ \ \ } \ Co_{(aq)}^{ \ 2+} \ + \ 2 \ Cl_{(aq)}^{ \ -}$
c. $AlCl_{3(s)} \ \xrightarrow{ \ \ \ \ eau \ \ \ \ } \ Al_{(aq)}^{ \ 3+} \ + \ 3 \ Cl_{(aq)}^{ \ -}$
d. $FeSO_{4(s)} \ \xrightarrow{ \ \ \ \ eau \ \ \ \ } \ Fe_{(aq)}^{ \ 2+} \ + \ SO_{4(aq)}^{ \ 2-}$
e. $FeBr_{3(s)} \ \xrightarrow{ \ \ \ \ eau \ \ \ \ } \ Fe_{(aq)}^{ \ 3+} \ + \ 3 \ Br_{(aq)}^{ \ -}$
g. $NaOH_{(s)} \ \xrightarrow{ \ \ \ \ eau \ \ \ \ } \ Na_{(aq)}^{ \ +} \ + \ HO_{(aq)}^{ \ -}$
um">h. $Al_2 \left( S_2O_4 \right )_{3(s)} \ \xrightarrow{ \ \ \ \ eau \ \ \ \ } \ 2 \ Al_{(aq)}^{ \ 3+} \ + \ 3 \ S_2O_{4(aq)}^{ \ 2-}$Exercice no 14 P96 : Calcul de la concentration des ions dans une solution.
1a.
$KCl_{(s)} \ \xrightarrow{ \ \ \ \ eau \ \ \ \ } \ K^{ \ +}_{(aq)} \ + \ Cl^{ \ -}_{(aq)}$
1b,c.
}D'après la réaction précédente, la quantité en ions $K^{ \ +}$ et $Cl^{ \ -}$ seront égales à celle de chlorure de potassium introduit. Leur concentrations en ions chlorure et potassium seront égales : $\left [ K^{ \ +}_{(aq)} \right ] \ = \ \left [ Cl^{ \ -}_{(aq)} \right ] \ = \ \dfrac{2,5.10^{ \ -3}}{0,200} \ = \ 1,25.10^{ \ -2} \ mol.L^{ \ -1}$
2a.
$AlCl_{3,(s)} \ \xrightarrow{ \ \ \ \ eau \ \ \ \ } \ Al^{ \ 3+}_{(aq)} \ + \ 3 \ Cl^{ \ -}_{(aq)}$
2b,c.
}D'après la réaction précédente, la quantité en ions $Al^{ \ 3+}$ sera égale à celle introduite en chlorure d'aluminium. Celle en ions chlorure sera le triple de celle introduite en chlorure d'aluminium.
$\left [ Al^{ \ 3+}_{(aq)} \right ] \ = \ \dfrac{5,0.10^{ \ -3}}{0,500} \ = \ 1,0.10^{ \ -2} \ mol.L^{ \ -1}$
$\left [ Cl^{ \ -}_{(aq)} \right ] \ = \ 3 \times \dfrac{5,0.10^{ \ -3}}{0,500} \ = \ 3,0.10^{ \ -2} \ mol.L^{ \ -1}$
Exercice no 15 P96 : Espèces miscibles en toutes proportions.
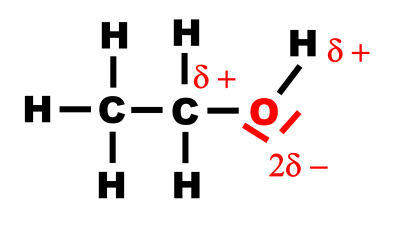
La différence d'électonégativiteé entre l'oxygène et le carbone implique une forte polarisation des liaisons Oygène - Carbone et Oygène - Hydrogène.
La molécule d'étanol étant donc polaire, de même, l'eau étant apolaire, les interactions entre les molécules seront importantes, ce qui explique le forte miscibilité de l'eau et de l'éthanol
Exercice no 18 P97 : Solubilité du vinaigre dans l'eau.
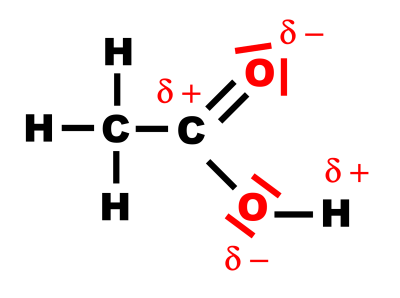
La différence d'électonégativiteé entre l'oxygène et le carbone implique une forte polarisation des liaisons Oygène - Carbone et Oygène - Hydrogène.
La molécule d'étanol étant donc polaire, de même, l'eau étant apolaire, les interactions entre les molécules seront importantes, ce qui explique le forte miscibilité de l'eau et de l'éthanol
Exercice no20 P97 : Mode d'action d'un savon.
1.

La chaine carbonée n'étant constituée que d'atomes de carbone et d'hydrogène n'est pas polaire, elle ne peut pas avoir d'interaction avec l'eau, d'où le terme "hydrophobe".
Le reste de la molécule, quant à elle est polaire, elle intéragit avec l'eau d'où le terme "hydrophyle".
2.
Le terme "amhiphile" car elle a une partie "hydrophyle" et une partie "hydrophobe.
3.
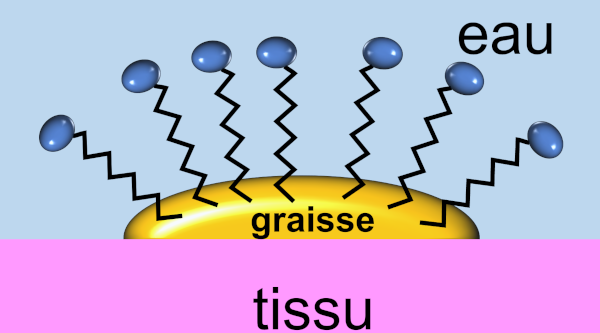
4.
La une partie "hydrophobe" intéragit avec la graisse. La partie "hydrophile" intéragit avec l'eau. Ainsi, la graisse est "entrainée" par l'eau.
Exercice no23 P98 : A propos du sulfate de sodium.
$Na_2S_2O{4(s)} \ \xrightarrow{ \ \ \ \ eau \ \ \ \ } \ 2 \ Na_{(aq)}^{ \ +} \ + \ S_2O_{4(aq)}^{ \ 2-}$
La quantité en ions sodium sera donc le double de celle en sulfate de sodium introduit, et celle est ions sulfate sera égale à celle en sulfate de sodium introduit.
La quantité de matière en soluté est : $n_{soluté} \ = \ \dfrac{m_{soluté}}{M_{soluté}} \ = \ \dfrac{2,5}{2 \times 23,0 + 1 \times 32,1 + 4 \times 16,0} \ = \ 1,76.10^{ \ -2} \ mol$
On a donc : $\left [ Na_{(aq)}^{ \ +} \right ] \ = \ 2 \times \dfrac{n_{soluté}}{V} \ = \ 2 \times \dfrac{1,76.10^{ \ -2}}{0,200} \ = \ 1,76.10^{ \ -1} \ mol.L^{ \ -1}$
et : $\left [ SO_{4(aq)}^{ \ 2-} \right ] \ = \ \dfrac{n_{soluté}}{V} \ = \ 2 \times \dfrac{1,76.10^{ \ -2}}{0,200} \ = \ 8,80.10^{ \ -2} \ mol.L^{ \ -1}$
Exercice no25 P99 : Préparation d'une solution de chlorure de fer III.
$FeCl_{3(s)} \ \xrightarrow{ \ \ \ \ eau \ \ \ \ } \ Fe_{(aq)}^{ \ 3+} \ + \ 3 \ Cl_{4(aq)}^{ \ -}$
La quantité de matière en ions fer III est la même que celle en chlorure de fer III introduit.
On souhaite que la concentration en ion fer III soit $\left [ Fe_{(aq)}^{ \ 3+} \right ] \ = \ 3,5.10^{ \ -2} \ mol.L^{ \ -1}$
Soit une quantité de matière : $n_{Fe} \ = \ c \times V \ = \ 0,200 \times 3,5.10^{ \ -2} \ = \ 7,0.10^{ \ -3} \ mol$
La quantité de matière introduite en soluté est donc : $n_{soluté} \ = \ n_{Fe}$
Soit une masse de soluté : $m_{soluté} \ = \ n_{Fe} \times M_{soluté} \ = \ 7,0.10^{ \ -3} \times \left (1 \times 55,8 + 3 \times 35,5 \ \right ) \ = \ 1,14 \ g$
Exercice no28 P100 : Solubilités.
1a.
La solubilité du chlorure de sodium est $s \ = \ 360 \ g.L^{ \ -1}$.
Dans 500 mL, on pourrait donc diluer $m \ = \ m \times V \ = 360 \times 0,5 \ = \ 180 \ g$.
Soit une quantité de matière $n \ = \ \dfrac{180}{23,1 + 35,5} \ = \ 3,07 \ mol \ > \ 2,56 \ mol$.
On pourra donc dissoudre les 2,56 mol dans 500 mL.
1b.
$NaCl_{(s)} \ \xrightarrow{ \ \ \ \ eau \ \ \ \ } \ Na^{ \ +}_{(aq)} \ + \ Cl^{ \ -}_{(aq)}$
1c.
D'après l'équation de dissolution ci-dessus, la quantité de matière en ion $Na^{ \ +}$ et $Cl^{ \ -}$ est la même que celle en chlorure de sodium dissout.
$\left [ Na^{ \ +} \right ] \ = \ \left [ Cl^{ \ -} \right ] \ = \ \dfrac{2,56}{0,5} \ = \ 5,12 \ mol.L^{ \ -1}$
2a.
La masse correspondante est : $m \ = \ 3,59.10^{ \ -2} \times \left ( 207,2 + 2 x 35,5 \right) \ = \ 10,0 \ g$
Si la totalité était dissoute, la concentration massique correspondante serait : $C_m \ = \ dfeac{10,0}{0,5} \ = 20 g/mol$
Cette valeur étant supérieure à la solubilité, la totalitré n'est pas dissoute.
La totalité ne serait pas dissoute, et pas homogène.
2b.
$PbCl_{2,(s)} \ \xrightarrow{ \ \ \ \ eau \ \ \ \ } \ Pb^{ \ 2+}_{(aq)} \ + \ 2 \ Cl^{ \ -}_{(aq)}$
Pour une mole de chlorure de plomb, on obtient 1 mole de $Pb^{ \ 2+}$ et 2 moles de $Cl^{ \ -}$.
La solubilité massique étant de $9,9 \ g.L^{ \ -1}$, soit : $\dfrac{9,9}{207,2 + 2 \times 35,5} \ = \ 3,56.10^{ \ -2} \ mol/L$.
Alors, $\left [ Pb^{ \ 2+} \right ] \ = \ 3,56.10^{ \ -2} \ mol/L$ et $\left [ Cl^{ \ -} \right ] [Cl-] \ = \ 2 \times 3,56.10^{ \ -2} \ = \ 7,1.10^{ \ -2} \ mol/L$.
2c.
La masse maximale dissoudre serait :$ m \ = \ 9,9 \times 0,5 \ = \ 5,95 \ g$.
Sur les 10,0 g introduits, $10,0 – 5,95 = 4,5 \ g$ ne le seront pas.
Exercice no29 P101 :Chlorure de sodium.
1a.
La distance entre les ions $Na^{ \ +}$ et $Cl^{ \ -}$ les plus proches est : $d_{Cl,Na} \ = \ r_{Na} \ + \ r_{Cl} \ = \ 97 + 181 \ = \ 278 \ pm$.
L'intensité de la force électrostatique attractive correspondante est : $F_{Cl,Na} \ = \ k \times \dfrac{e^2}{d_{Cl,Na}^2} \ = \ 3,0.10^{ \ -9} \ N$
La distance la plus petite séparant deux ions $Na^{ \ +}$ est : $d_{Na,Na} \ = \ \left ( r_{Na} + r_{Cl} \right ) \times \sqrt{2} \ = \ 393 \ pm$.
L'intensité de la force électrostatique répulsive correspondante est : $F_{Na,Na} \ = k \times \dfrac{e^2}{d_{Na,Na}^2} \ = \ 7,5.10^{ \ -10} \ N$
1b.
L'intensité de la force électrostatique attractive étant supérieure à l'intensité de la force électrostatique, le solide est cohérent.
2a.
Le rapport de la force d'interaction entre deux ions dans le cristal solide à la force d'interaction entre deux ions dans l'eau est : $\dfrac{F_{sol}}{F_{eau}} \ = \ \dfrac{k_{sol} \times \dfrac{e^2}{d^2}}{k_{eau} \times \dfrac{e^2}{d^2}} \ = \ \dfrac{k_{sol}}{k_{eau}} \ = \ \dfrac{9.10^{ \ 9}}{1,1.10^{ \ 8}} \ = \ 82$
2b.
La valeur des forces étant 82 fois plus faible dans l'eau que dans le solide, il y sera facilement dissout.
Exercice no36 P102 : Mélange.
|
Solution de chlorure de sodium. $NaCl_{(s)} \ \xrightarrow{ \ \ \ \ eau \ \ \ \ } \ Na_{(aq)}^{ \ +} \ + \ Cl_{(aq)}^{ \ -}$ La quantité de matière en $Cl^{ \ -1}$ est : $n_1 \ = \ C_1 \times V_1$ $n_1 \ = \ \dfrac{C_{m,1} \times V_1}{M_{NaCl}}$ $n_1 \ = \ \dfrac{0,6 \times 20.10^{ \ -3}}{35,5 + 23,1} \ = \ 2,05.10^{ \ -4} \ mol$ |
Solution de chlorure de calcium. $CaCl_{2,(s)} \ \xrightarrow{ \ \ \ \ eau \ \ \ \ } \ Ca_{(aq)}^{ \ 2+} \ + \ 2 \ Cl_{(aq)}^{ \ -}$ La quantité de matière en $Cl^{ \ -1}$ est : $n_2 \ = \ 2 \times C_2 \times V_2$ $n_2 \ = \ 2 \times \dfrac{C_{m,2} \times V_2}{M_{CaCl_2}}$ $n_2 \ = \ 2 \times \dfrac{1,4 \times 5.10^{ \ -3}}{2 \times 35,5 + 40,1} \ = \ 6,30.10^{ \ -5} \ mol$ |
La concentration totale en ions chlorure est :
$\left [ Cl^{ \ -} \right ] \ = \ \dfrac{n_1 + n_2}{V_1 + V_2} \ = \ 1,3.10^{ \ -2} \ mol.L^{ \ -1}$
Ajouter un commentaire
