Composition d'un système chimique : exercices
Exercice n°8 : Masse molaire atomique du carbone.
1. Dans une mole d'atomes de carbone, il y a $N_a=6,02.10^{ \ 23}$ (constante d'Avogadro) atomes de carbone.
2. La masse molaire atomique du carbone est donc : $M(C) =6,02.10^{ \ 23} \times 1,99.10^{ \ -23} = 12,0 \ g.mol^{ \ -1 }$.
3. On retrouve cette valeur dans la classification périodique des éléments.
Exercice n°10 : Utilisation du tableau périodique des éléments.
| Entité chimique | Formule brute | Masse molaire (g/mol) |
| Méthane | $CH_4$ | $1 \times 12 +1 \times 1 = 16$ |
| Ion fluorure | $F^{ \ -}$ | $19$ |
| Ethanol | $C_2H_6O$ | $12 \times 2 + 6 \times 1 + 1 \times 16 = 16$ |
| Ammoniac | $NH_3$ | $1 \times 14 + 3 \times 1 = 14$ |
Exercice n°11 : Masses molaire atomique.
La masse molaire d'une entité correspondant à la masse d'une mole de cette entité la relation entre la masse molaire M de cette entité et la masse m de cette entité est : $M = m \times N_a$, où $N_a$ est la constante d'Avogadro.
| Entité chimique | Masse (g) | Masse molaire (g.mol-1) |
| proton | $1,67.10^{ \ -27}$ | $M= 1,67.10^{ \ -27} \times N_a = 1,00 $ |
| atome de sodium | $m = \dfrac {23}{N_a} = 3,82.10^{ \ -23}$ | $23,0$ |
| molécule d'eau | $2,99.10^{ \ -23}$ | $M= 2,99.10^{ \ -23} \times N_a = 18,0 $ |
| bille | $m = \dfrac {1,24.10^{24}}{N_a} = 2,06$ | $1,24.10^{ \ 24}$ |
| ion magnésium | $4,04.10^{ \ -23}$ | $M=4,04.10^{ \ -23} \times N_a = 24,3 $ |
Exercice n°15 : Le sucre.
1. $M \left ( C_{12}H_{12}O_6 \right ) =12 \times 12,0 + 12 \times 1,0 + 11 \times 16,0 = 332 g.mol^{ \ -1} $.
2. $ m = 10 \times M = 10 \times 332 = 3320 g $.
Exercice n°16 : Vitamine C.
1. $M \left ( C_{6}H_{8}O_6 \right ) =6 \times 12,0 + 8 \times 1,0 + 6 \times 16,0 = 176 g.mol^{ \ -1} $.
2. $ n = \dfrac {m}{M} \ = \ \dfrac {500.10^{ \ -3}}{176} = 2,84.10^{ \ -3} mol $.
Exercice n°19 : Volume molaire et quantité de matière.
La relation entre le volume molaire $V_m$ d'un gaz, le volume $V$ et la quantité de matière $n$ est : $V_m = \dfrac {V}{n}$
| Echantillon | 1 | 2 | 3 |
| Volume molaire $ \left( en \ L.mol^{ \ -1} \right)$ | 24 | 22,4 | $V_m = \dfrac {5000}{58,8} =85,0$ |
| Volume de l'échantillon $ \left( en \ L \right)$ | 1,5 | $n = 2,23 \times 22,4 = 50,0$ | 5000 |
| Quantité de matière $ \left( en \ mol \right)$ | $n = \dfrac {1,5}{24}=6,25.10^{-2}$ | 2,23 | 58,8 |
Exercice n°23 : Traceur sanguin.
1,2.
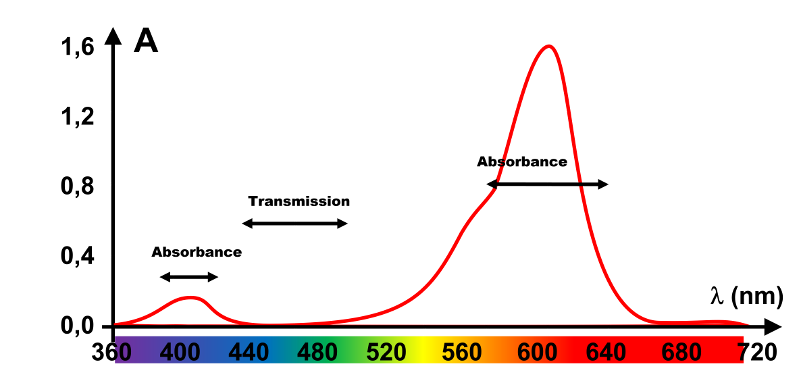
Les longueurs d'onde absorbées se situent dans les intervalles $ \left [ 380;430 \right ]$ (bleu) et $\left [ 600;680 \right ]$ (rouge),
celles transmises, dans l'intervalle $\left [ 450 ; 500 \right ]$ (vert).
3. La solution absorbant le bleu et le rouge, elle transmet le vert, on la verra verte.
Exercice n°24 : Préparation d'un dosage.
1. Protocole.
• S'équiper du matériel de sécurité : blouse, gants, lunettes
• Matériel nécessaire :
Pour le prélèvement de la solution mère : bécher contenant la solution mère, pipettes jaugées ou graduées ou éprouvettes graduées aux volumes appropriés, ou burette.
Pour la dilution : fioles aux volumes appropriés.
Pissette d'eau distillée.
• Prélever le volume nécessaire et l'introduire dans la fiole. Ajouter de l'eau distillée et homogénéiser le mélange. Compléter au trait de jauge, homogénéiser et compléter au trait de jauge.
2. La grandeur qui ne change pas est la quantité de matière prélevée.
3.
La quantité de matière étant conservée, on a forcément : $C_{mère} \times V_{mère} = C_{fille} \times V_{fille}$
soit : $C_{fille} = \dfrac {C_{mère} \times V_{mère}}{V_{fille}}$
| Solution fille | 1 | 2 | 3 | 4 |
| Volume prélevé (mL) | 10 | 20 | 30 | 40 |
| Volume final (mL) | 50 | 50 | 50 | 50 |
| Concentration finale $\left( \mu mol.L^{ \ -1} \right)$ | 6,8 | 13,6 | 20,4 | 27,2 |
Exercice n°25 : Loi de Beer-Lambert.
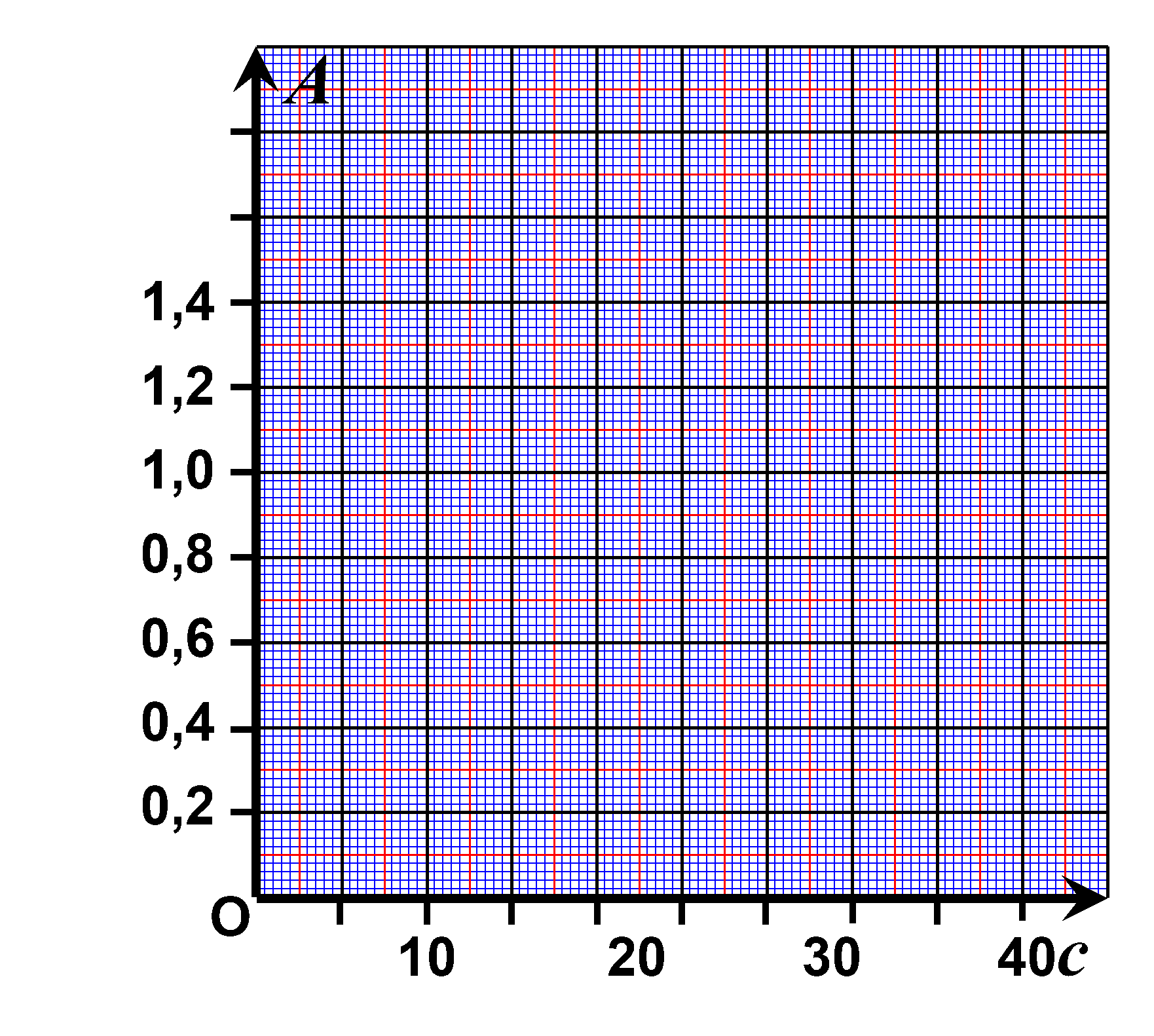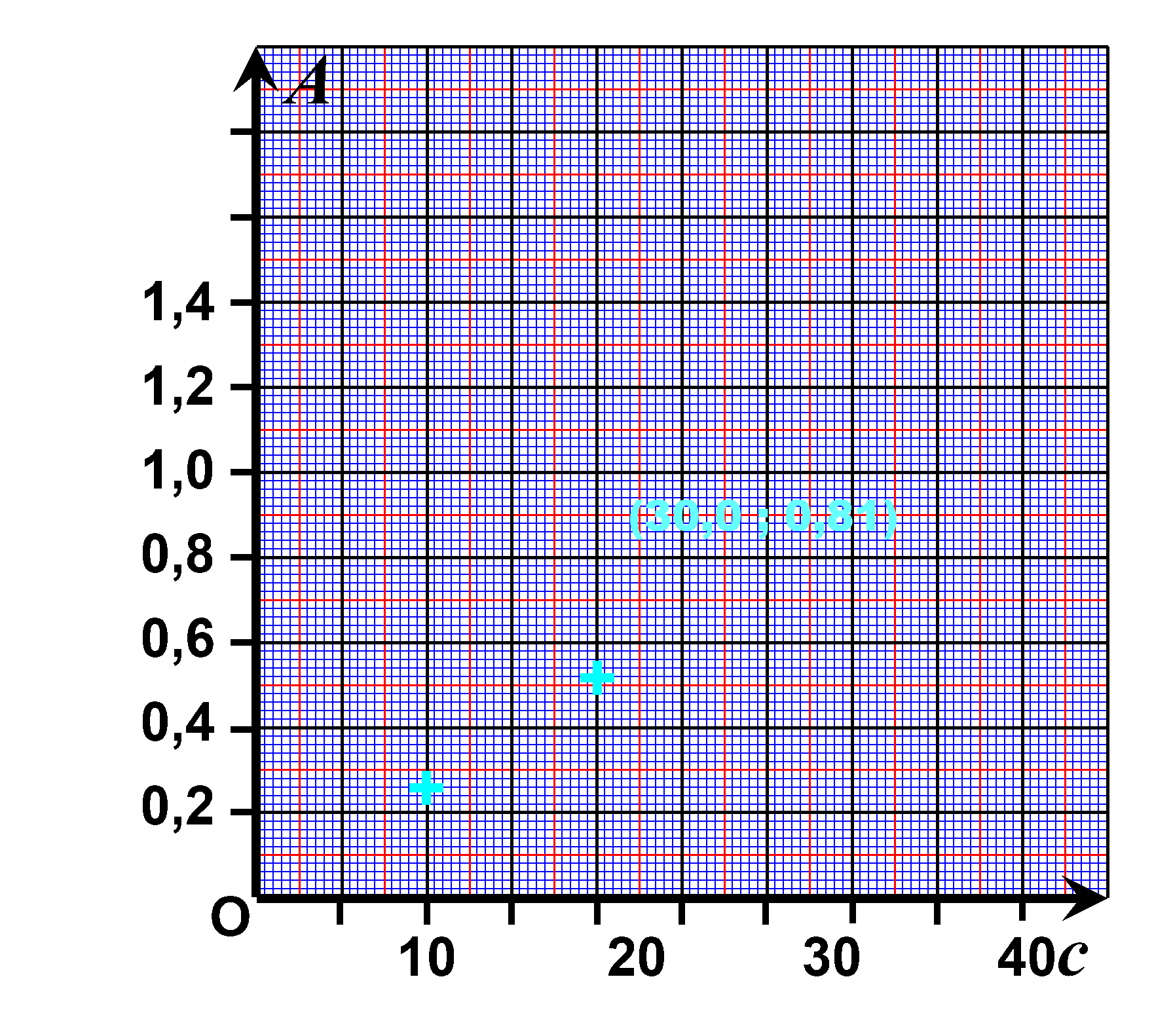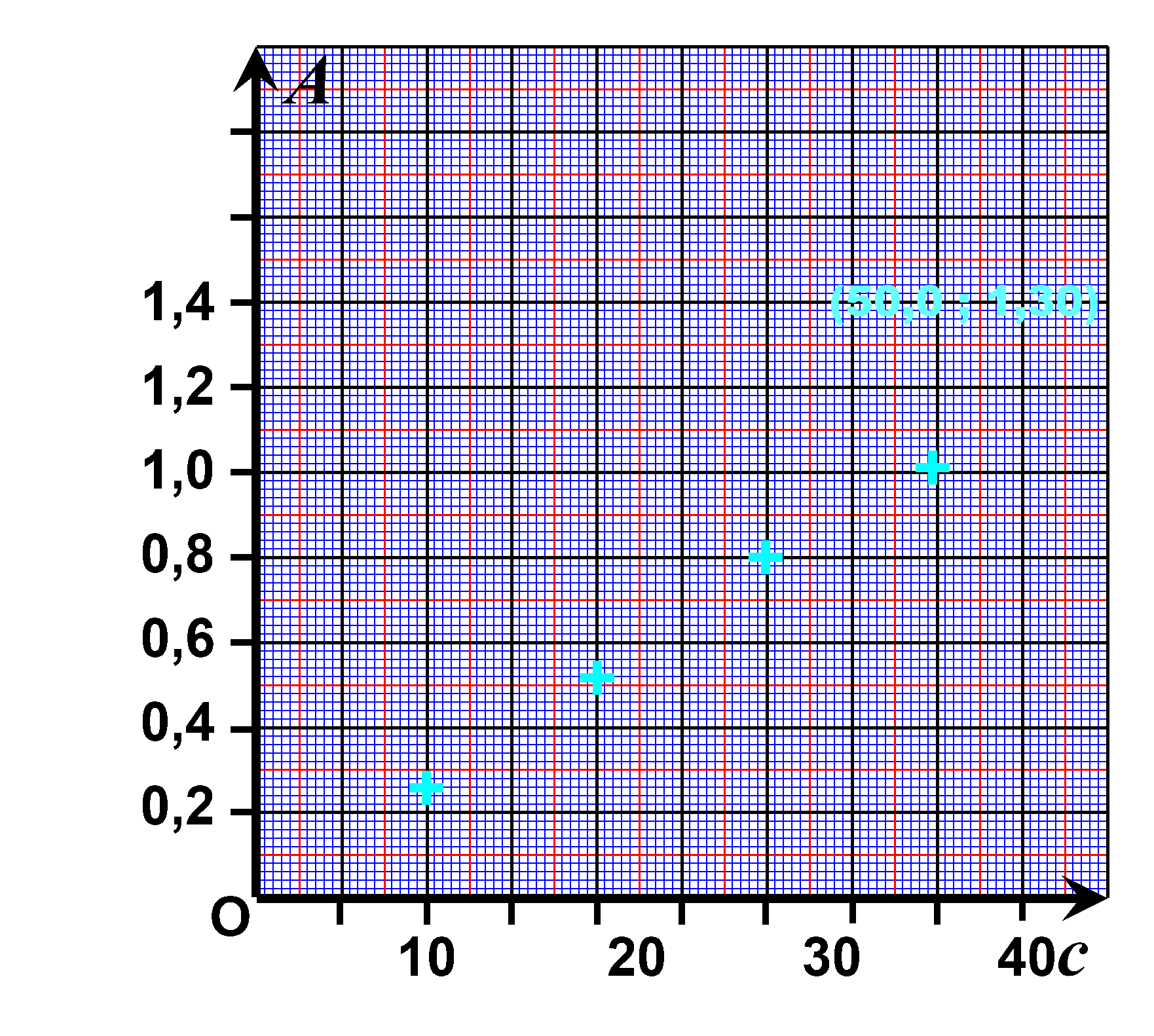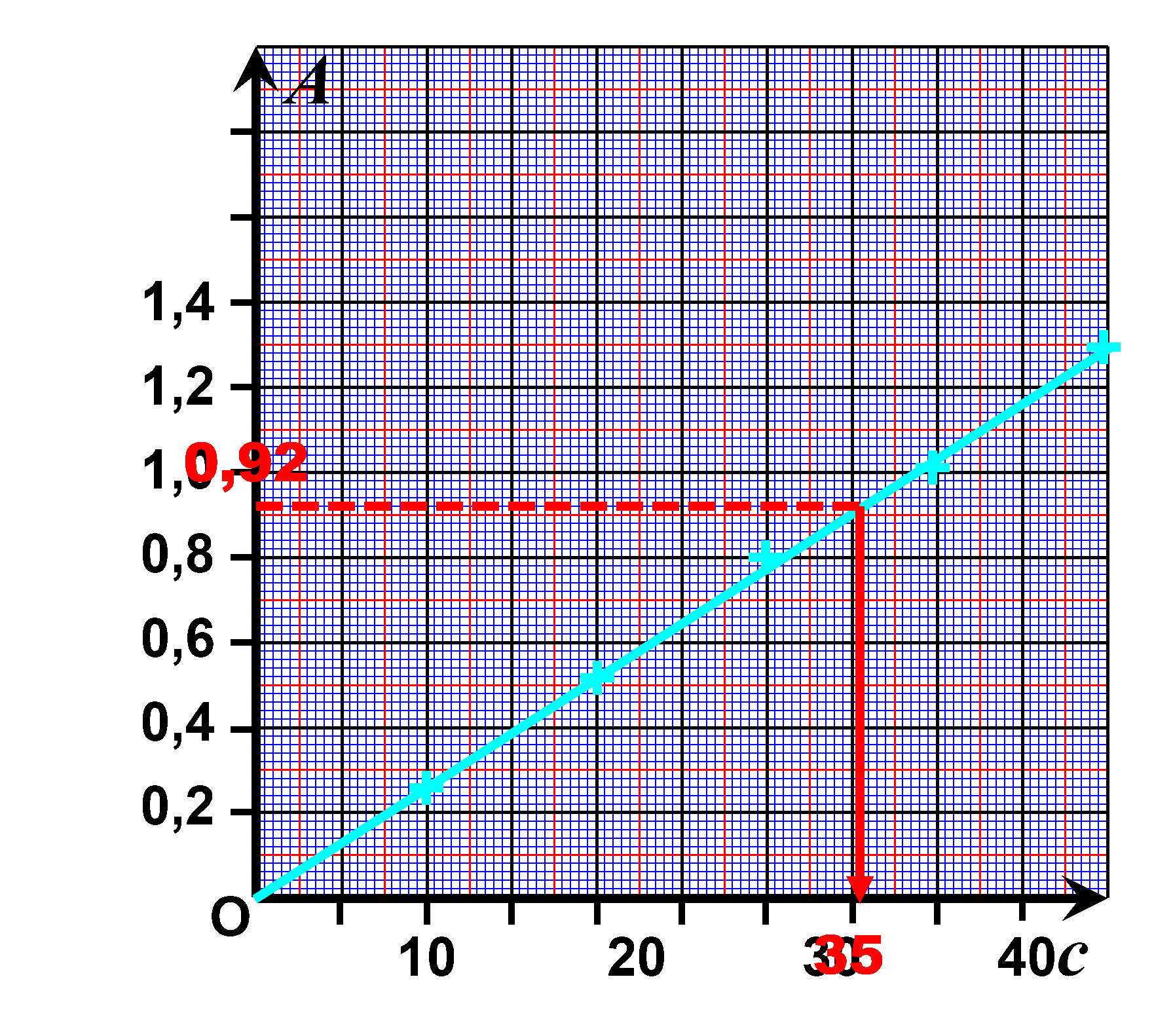
Les points sont alignés.
On vérifie la loi de Beer-Lambert : l'absorbance est proportionnelle à la concentration $A= k \times c$
Sur le graphique, pour une absorbance $A_s=0,92$ on lit une concentration $c_s = 35 \ \mu mol^{ \ -1}$
Exercice n°26 : Dosage par étalonnage.
1.
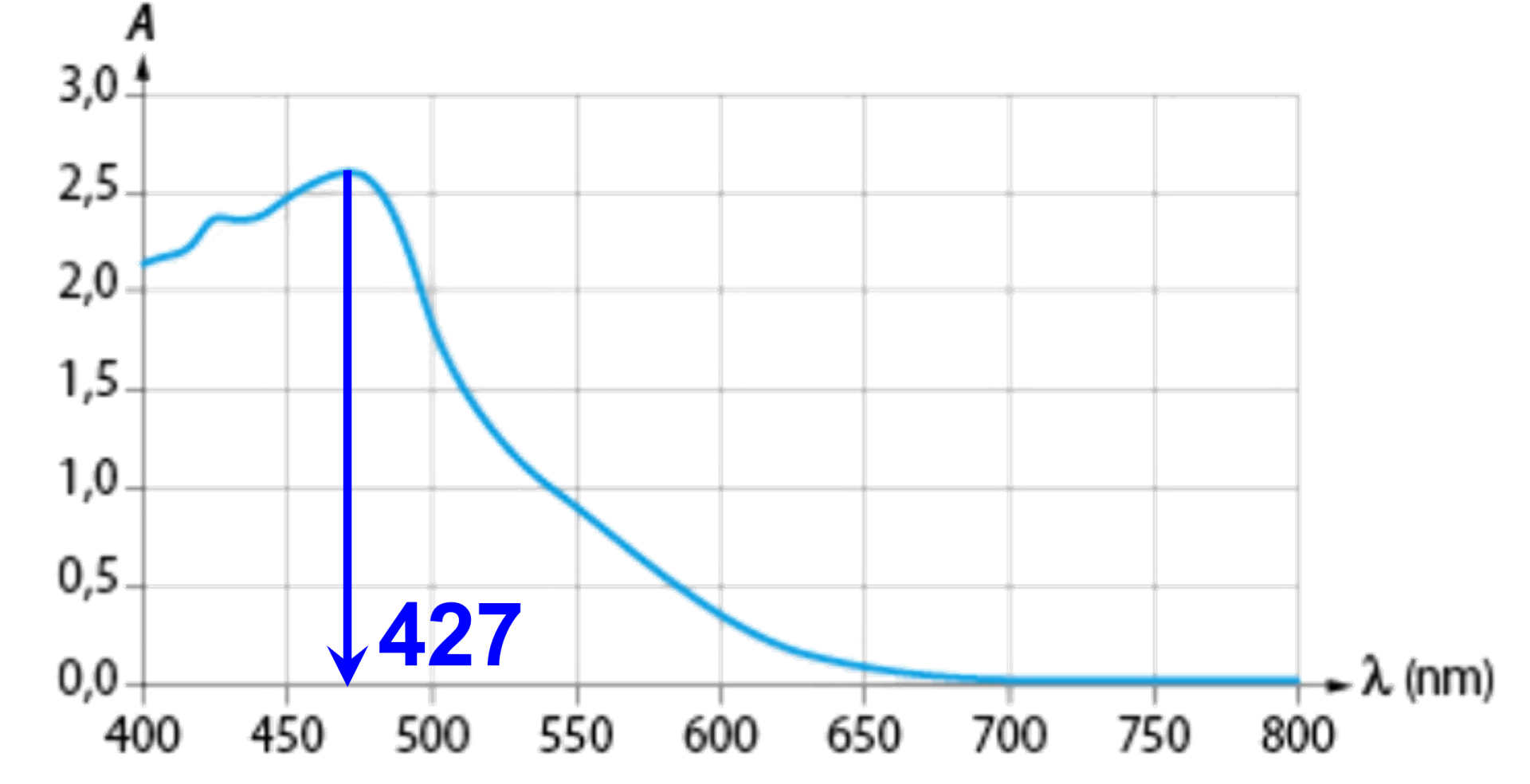
Sur le graphique, on lit une absorbance maximale à la longueur d'one $\lambda \ = \ 427 \ nm$.
On règlera le spectrophotmètre à cette longueur d'onde. L'absorbance diminuera au cours des dilutions successives. Etant maximale, la valeur à mesurer sera plus précise.
2.
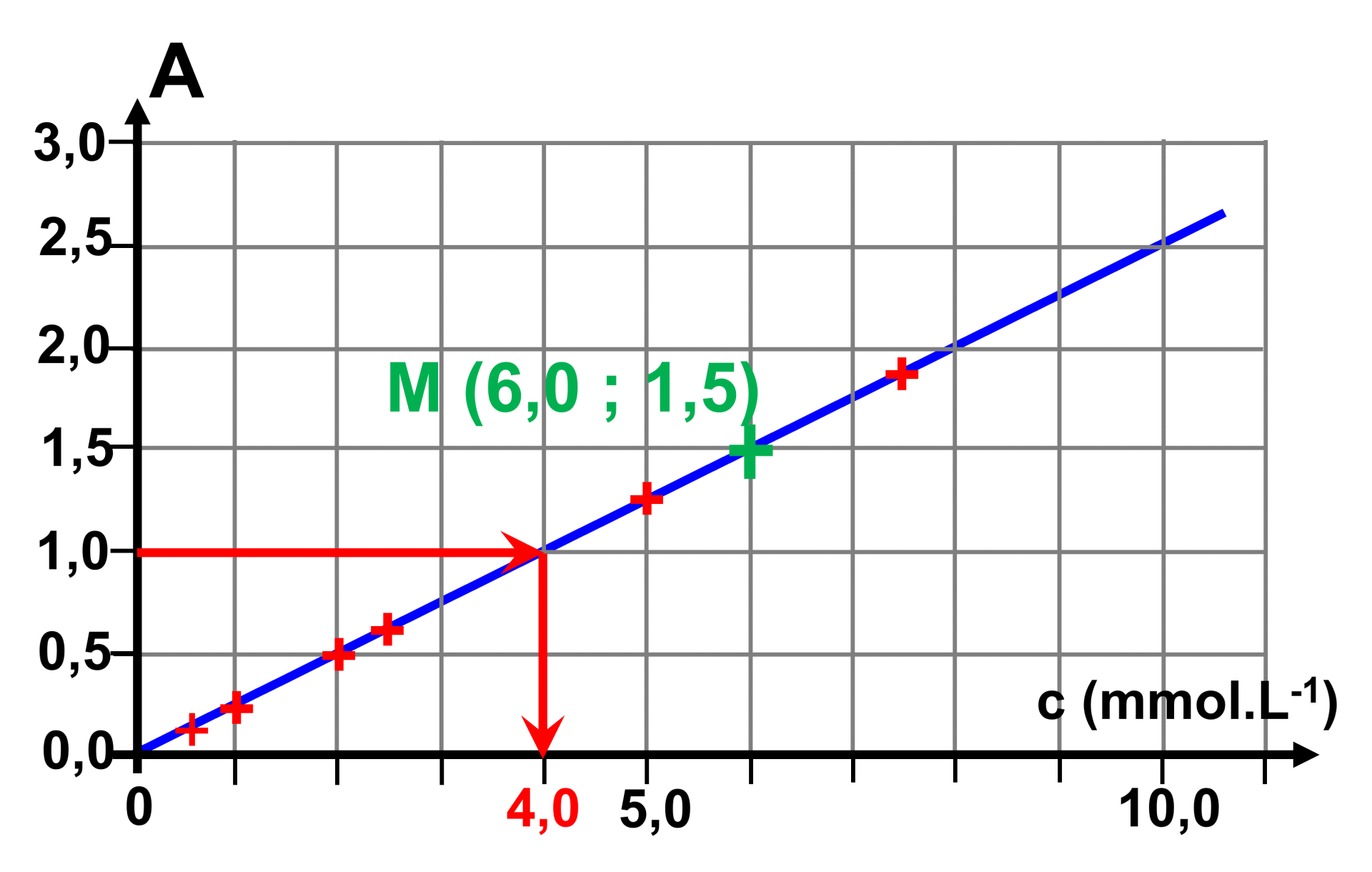
Le graphe montre une droite linéaire. L'absorbance est proportionnelle à la concentration : $A \ = \ k \times c$.
En choisissant par exemple le point $M(6,0 ; 1,5)$ on détermine un coefficient $k \ = \ \dfrac{1,5}{6,0} \ = \ 0,25$. on a alors : $A \ = \ 0,25 \times c$
3.
Pour la solution diluée 10 fois, on en déduit : $c_{diluée} \ = \ \dfrac{1,0}{0,25} \ = \ 4,0 \ mmol.L^{ \ -1}$
4.
La solution ayant été diluée 10 fois, la concentration en lugol de la solution initiale est : $c_{commerciale} \ = \ 10 \times 4,0 \ = \ 40 \ mmol.L^{ \ -1}$
Exercicen° 35 : Bouillie bordelaise.
1.la masse volumique est : $\rho = 1,5 \ kg.L^{ \ -1}$. Cela signifie qu'un litre de solution a une masse de $1,5 \ kg$. Cette solution à $20 \ %$ contient donc une masse $m \ = \ 1,5 \times \dfrac{20}{100} \ = \ 0,3 \ kg$
2.La masse molaire du cuivre est m $M(Cu) \ = \ 63,5 \ g.mol^{ \ -1}$. La qauntité de matière corresondant est donc : $n \ = \ \dfrac{m}{M} \ = \ \dfrac{300}{63,5} \ = \ 4,72 \ mol$
3.La dissociation du sulfate de cuivre s'écrit : $ CuSO_{4,s} \ \overset{ \ \ \ eau \ \ \ }{ \longrightarrow} \ Cu^{ \ 2+}_{(aq)} \ + \ SO_{4(aq)}^{ \ 2-}$
La quantité de matière en sulfate de cuivre est la même que celle en ion $Cu^{ \ 2+} \ : \ n{CuSO_4} \ = \ 4,72 \ mol$.
La concentration molaire est donc : $c_{CuSO_4} \ = \ 4,72 \ mol.L^{ \ -1}$.
Soit une conentration massique :
$c_m \ = \ c \times M_{CuSO_4} \ = \ 4,72 \times \left ( 1 \times 63,5 + 1 \times 32,1 \ + 4 \times 16,0 \right ) \ = \ 754 \ g.L^{ \ -1}$.
Exercicen°43 : Les sucres du miel.
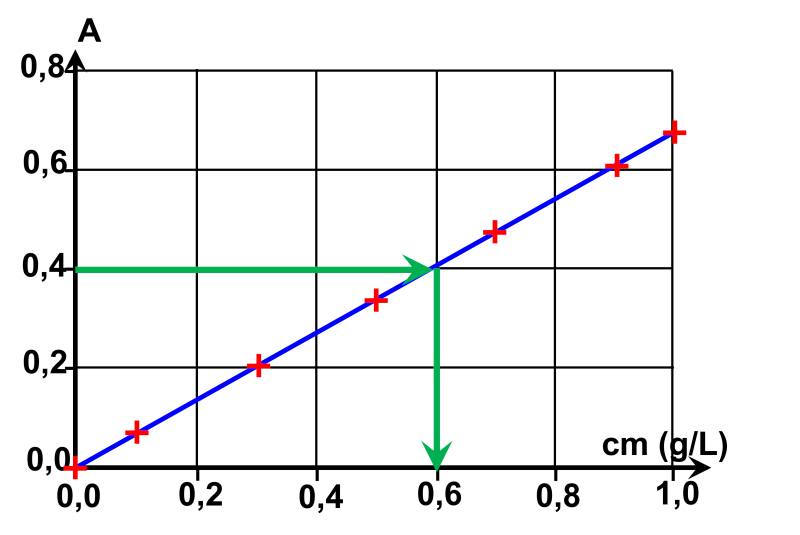
1. Pour une absorbance $A = 0,40$, on lit une concentration massique $c_m \ = \ 0,6 \ g/L$
2. La valeur déterminée est celle de la solution préparée obtenue après une dilution au dixième.
La solution initiale a donc une concentration $c_{m,initiale} = 10 \times c_m \ = 6 \ g/L$.
La masse de sucre correspondant dans la solution $V=50 \ mL$ est donc : $m = c_{m,initiale} \times V = 6 \times 50.10^{ \ -3} = 0,3 \ g$.
Synthèse :
Cette masse de sucre est contenue dans le prélèvement de $0,6 \ g$.
Cette masse de sucre représente : de $\dfrac{0,3}{0,6} \times 100 = 50 \% $ de la masse du prélèvement.
La teneur doit être au minimum de $45 \%$. Le miel n'est pas frelaté.
Exercicen°44 : Homéopathie.
Une solution $1CH$ étant obtenue par dilution de 1 goutte dans 99 gouttes. Cela correspond à une dilution au $100^{ \ ème}$
Une solution $2CH$ correspond à une dilution au $100^{ \ ème}$ de la solution elle-même diluée 100 fois. Dans ce cas, la solution mère a été diluée $100 \times 100 = \left ( 10^{ \ 2} \right ) ^2 \ = \ 10^ { \ 4}$ fois
Une solution $9CH$ a été diluée :$\left ( 10^2 \right ) ^9 \ = 10^{ \ 18}$ fois
La solution mère ayant une concentration $c_{mère} \ = \ 1 \ mol^{ \ -1}$, la solution $9CH$ a pour concentration : $c_{9CH} = \dfrac{1}{10^{ \ 18}} \ = \ 10^{ \ -18} \ mol.L^{ \ -1}$
Soit une quantité en principe actif dans les 10 mL : $n_{9CH} = c_{9CH} \times 10.10^{ \ -3} = 10^{ \ -20} \ mol$
La quantité d'entités correspondant est : $N = n_{9CH} \times {\cal{N}_a} \ = 10^{ \ -20} \times 6,02.10^{ \ 23} = 6,02.10^{3} = 6020$ molécules
Ajouter un commentaire
