Fluide au repos

Exercice 8 P209 :

1a, b. Les molécules sont à l'état gazeux car les molécules ne sont pas en contact, contrairement à l'état liquide ou solide.
2. Les molécules d'eau dans le liquide se déplacent beacoup moins, car elles sont en contact les une avec les autres, ce qui réduit leur déplacement.
3. Les molécules d’eau vont sortir de l’erlenmeyer, celles qui entreront en contact avec la paroi vont se condenser.

Exercice 10 P209 : Température et pression à la loupe.

1. L'été, la température augmente au cours de la journée, le ballon s'est dilaté. Les molécules constituant l'air sont plus agitées.

2. Les chocs entre les molécules augmentent, le nombre de chocs se traduit par l’augmentation de température.

3a. C’est la pression : les molécules viennent frapper sur les parois du ballon.

3b. La température a augmenté, de fait la pression a augmenté.

Exercice 12 P209 : Air dans une seringue.

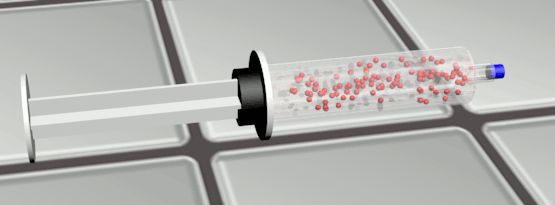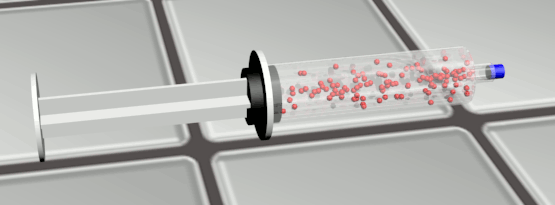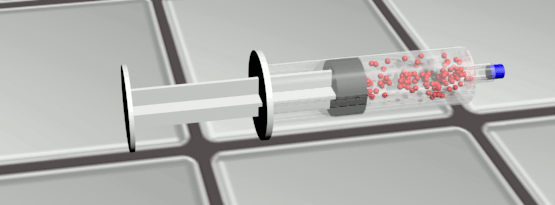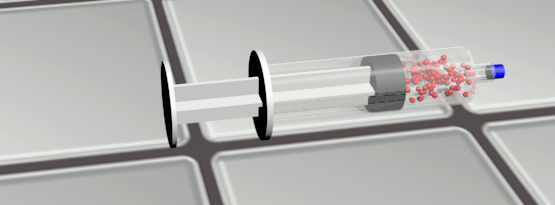
1a.  Le volume, la pression et la température supposée constante ici.

1b. Le volume diminue, la pression augmente.

2a. Les molécules se rapprochent, les chocs sur les parois vont augmenter. La pression augmente.

2b.  D'après la loi de Mariotte : $P \times V \ = \ Cste$. Le volume diminuant, la pression augmentera. En accord avec les réponses précédentes.

Exercice 13 P209 : Densité moléculaire.

1.  A l'état gazeux, pour une quantité de molécules donnée, les molécules disposent d'un volume plus important qu'à l'état liquide.

La masse volumique est donc plus importante à l'état liquide qu'à l'état.

2a.  

La densité moléculaire est beaucoup plus faible à l'état gazeux qu'à l'état liquide. $N_1$ et $N_2$ étant du même ordre de grandeur, il s'agit des densités moléculaires des corps à l'état liquide. La plus faible $N_3$ correspond à celle du diazote gazeux.

2b.  

La densité moléculaire $N$ correspond au nombre de molécules par $m^{ \ 3}$.

La quantité de matière par $m^{ \ 3}$ est donc : $n \ = \ \dfrac{N}{N_a}$.

La masse volumique est : $\rho \ = \ \dfrac{N}{N_a} \times M$.

$\bullet$ En associant $N_{ \ 1}$ au diazote $N_2$, on trouve : $\rho \ = \ \dfrac{1,7 \times 10^{ \ 28}}{6,02 \times 10^{ \ 23}} \times \left ( 2 \times 14 \times 10^{ \ -3} \right ) \ = \ 791 \ kg.m^{ \ -3} \ $ .

$\bullet$ En associant $N_{ \ 2}$ à l'eau $H_2O$, on trouve : $\rho \ = \ \dfrac{3,3 \times 10^{ \ 28}}{6,02 \times 10^{ \ 23}} \times \left ( 18 \times 10^{ \ -3} \right ) \ = \ 987 \ kg.m^{ \ -3} \ $ .

La densité moléculaire de l'azote liquide est donc $N_1$, et celle de l'eau liquide est $N_2$

Exercice 14 P210 : Force pressante exercée par l'air atmosphérique.

1. L'origine microscopique de cette action est l'agitation moléculaire des molécules constituant le gaz à l'intérieur du flacon

2.

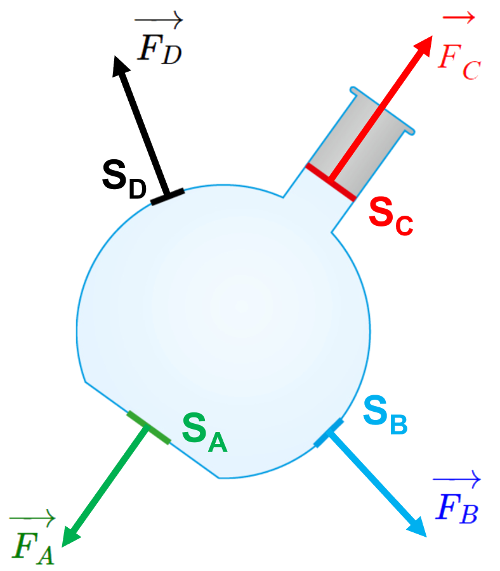
Exercice 15 P210 : Calcul de force pressante.

1. La relation liant la pression $P$ exprimée en Pascal (Pa), la surface $S$ exprimée en $m^2$ et la force $F$ exprimée en Newton (N) est : $P \ = \ \dfrac{F}{S}$

2a. Si la surface est doublée, la force $F \ = \ P \times S$ est doublée.

2b. Si la pression est divisée par 2, la force est divisée par 2.

3. $F \ = \ P \times S \ = \ 1083,3.10^{ \ 2 }  \times 1,5 \ = \ 1,62.10^{ \ 5 } \ N$.

Exercice 16 P210 : Des grandeurs interdépendantes.

Cas n°1 : $F_1 \ = \ P_1 \times S_1 \ = 1,013 \times 10^{ \ 5} \times 2,0 \times 10^{ \ -4} = \ 20,3 \ N$

Cas n°2 : $P_2 \ = \ \dfrac{F_2}{S_2} \ = \ \dfrac{4,5.10^{ \ 3 }}{2,5 \times 10^{ \ -2}} \ = 1,4.10^{ \ 5 } \ Pa \ = \ 1400 \ hPa$

Cas n°3 : $S_3 \ = \ \dfrac{F_3}{P_3} \ = \ \dfrac{9,2.10^{ \ 2 }}{3,6.10^{ \ 2 }} \ = \ 0,025 \ m^{ \ 2 } \ = \ 250 \ cm^{ \ 2}$

Exercice 17 P210 : Variation de volume en plongée.

1a. D'après la loi de Mariotte : $P \times V = k \ \Leftrightarrow \ V \ = \ \dfrac{k}{P} $ : le volume est inversement proportionnel à la pression.

1b. $P_C \times V_C = P_A \times V_A \ donc : V_A \ = \  \dfrac{P_C \times V_C}{P_A} \ = \ \dfrac{4,0 \times 1}{2} \ = \ 2,0 \ L$.

2a. $P_C \times V_C = P_B \times V_B$.

2b. $ V_B \ = \  \dfrac{P_C \times V_C}{P_B} \ = \ \dfrac{4,0 \times 1}{3} \ = \ 1,3 \ L$.

3. $ V_0 \ = \  \dfrac{P_C \times V_C}{P_0} \ = \ \dfrac{4,0 \times 1}{1} \ = \ 4,0 \ L$.

Exercice 19 P210 : Modéliser le comportement d'un gaz.

En traçant la courbe $V \ = \ f(P)$, on obtient le modèle suivant :

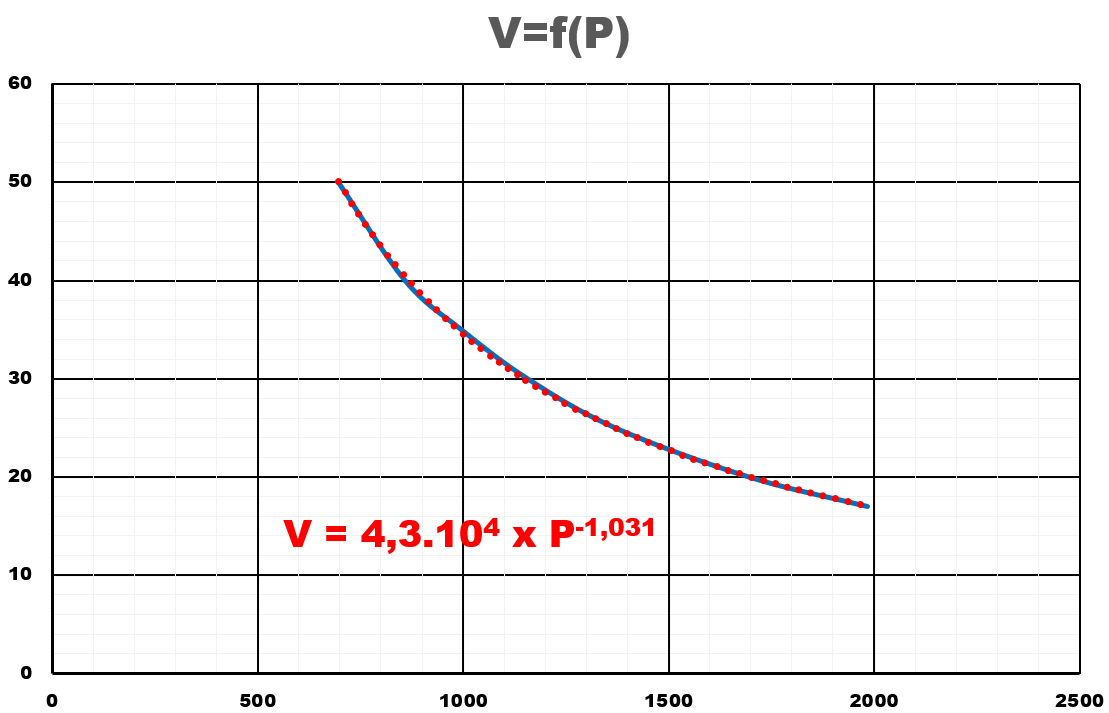
$V \ = \dfrac{4,3.10^{ \ 4}}{P}$ soit : $P \times V \ = \ 4,3.10^{ \ 4}$

La loi de mariotte est bien vérifiée.

Exercice 21 P211 : Statique des fluides dans l'eau de mer.

1a. D'après la loi de la statique des fluides : $\Delta P \ = \ \rho .g. \Delta h$

En prenant $\rho_{eau \ de \ mer} \ = \ 1025 \ kg.m{ \ -3}$, on a :$\Delta P \ = \ 1025 \times 9,81 \ times 3,0.10^{ \ 4} \ Pa$

1b. $P_B \ = \ P_A + \Delta P \ = \ 1,013.10^{ \ 5} + 3,0.10^{ \ 4} \ = 1,3.10^{ \ 5} \ Pa$

2a. Les B et C étant à la même profondeur, la différence de pression entre A et C sera la même. La pression en B et C est la même.

2b. Pour que la pression en C soit supérieure à celle en B, il faudra que la différence de profondeur entre A et C soit plus importante. Il faudra placer le point C à une profondeur plus importante.

Exercice 23 P211 : Variation de la pression en plongée.

1a,b. D'après la loi de la statique des fluides : $P_A - P_{atm} \ = \  \rho \times g \times \left ( z_0 - z_A \right )$

1c. $P_A \ = \  \rho \times g \times \left ( z_0 - z_A \right ) +  P_{atm} \ = 1025  \times 9,81 \times 10 \ +   \ 1013.10^{ \ 2} \ = \ 2,02.10^{ \ 5} \ Pa$

2a. $P_A - P_B  \ = \  \rho \times g \times \left ( z_B - z_A \right ) $

2b. $z_B \ = \  \dfrac{P_A - P_B}{rho \times g} + z_A \ = \ \dfrac{2,02.10^{ \ 5} - 3,0.10^{ \ 5}}{1025 \times 9,81} - 10 \ = \ -19,8 \ m $

Exercice 24 P211 : Principe du baromètre à liquide.

1a. La pression au sein d'un fluide étant la même à une hauteur donnée, on a : $P(z_1) \ = \ P_1$ et $P(z_2) \ = \ P_2$.

D'après la loi de la statique des fluides : $P_1 + \rho \times g \times z_1 \ = \  P_2 + \rho \times g \times  z_2$.

Soit : $ P_1 \ - \ P_2= \ \rho \times g \times  \left ( z_2 - z_1 \right ) \ = \ \rho \times g \times h$.

1b.  $ P_1  \ = \  \ \rho \times g \times h + P_2$.

Si $h$ augmente, $P_1$ augmente aussi.

2.  $ \Delta P \ = \ P_1 \ - \ P_2 \ = \ 1,013.10^{ \ 5} \ Pa$.

D'après l'expression précédente : $h \ = \ \dfrac{ P_1 \ - \ P_2}{\rho \times g}$

2a.  Dans le cas de l'eau, $\rho \ = \ 1000 \ kg.m^{ \ -3}$ donc : $P_1 \ - \ P_2 \ = \ 1,013.10^{ \ 5} \ Pa$.

On aura : $h \ = \ \dfrac {\Delta P}{\rho \times g}  \ = \ \dfrac {1,013.10^{ \ 5}}{1000 \times 9,81} \ = \ 10,3 \ m $.

2b.  Dans le cas du mercure , $\rho \ = \ 1,36.10 ^{ \ 4} \ kg.m^{ \ -3}$.

On aura : $h \ = \ \dfrac {\Delta P}{\rho \times g}  \ = \ \dfrac {1,013.10^{ \ 5}}{1,36.10^{ \ 4} \times 9,81} \ = \ 0,76 \ m $.

D'où l'intérêt d'utiliser un baromètre à mercure plutôt qu'un baromètre à eau.

Exercice 26 P212 : Effet de la pression en plongée.

1.  $P-P_{atm} \ = \ \rho \times g \times z.$. La profondeur augmentant la différence de pression augmente. D'après la loi de Mariotte, le produit $P \ V$ étant constant, le volume des poumons diminue.

2a.  $V \ = \ 4 \pi \dfrac{R^{ \ 3}}{3} \ = \ 4 \pi \dfrac{10^{ \ 3}}{3} \ = \ 4,2.10^{ \ 3} \ cm^{ \ 3} \ = \ 4,2 \ L$

2b.  La pression est : $P \ = \ \dfrac{P_{atm} \times V_{atm}}{V}$.

La profondeur est donc : $z \ = \ \dfrac{P- P_{atm}}{ \rho \times g} \ = \ \dfrac{P_{atm}}{\rho \times g} \times \left ( \dfrac{V_{atm}}{V} -1 \right ) \ = \ \dfrac{1,013.10^{ \ 5}}{1,03.10^{ \ 3} \times 9,81} \times \left ( \dfrac{6}{4,2} -1 \right ) \ = \ 4,3 \ m$

Exercice 29 P214 : Le baromètre de Torricelli.

1.  $z_A \ = \ 760 \ mm$.

2a.  Le mercure dans le tube descend sous l'effet de son poids. La totalité ne desend pas à cause de la pression exercée par l'air à la surface du mercure dans la cuve.

2b.  $P_A \ = \ P_{atm} $. 

3a.  $P_A + \rho_{Hg} \times g \times z_A \ = \ P_B + \rho_{Hg} \times g \times z_B$, soit : $P_B = \ P_A + \rho_{Hg} \times g \times \left (z_A \ - z_B \right )$.

3b.   $P_B = \ 1,03.10^{ \ 5 }  + 1,36.10^{ \ 4}  \times 9,81 \times \left (-760.10^{ \ -3} \right ) \ = \ -96,16 \ Pa$.

3c.   On obtient une valeur négative, mais très faible comparée à la pression atmosphérique : $\dfrac { \left | -96,16 \right |}{ 1,03.10^{ \ 5 }} \ = \   9,5.10^{ \ -4}$. On peut donc considérer que la pression au point B est identique à la pression atmosphérique.

En effet, la partie supérieure du tube est vide : aucune pression ne s'exerce sur le fluide au point B autre que celle due à l'agitation des particules constituant le fluide identique à celle due à l'agitation des particules au point A.

4a.  Du fait de l'équilibre du sytème, la somme des forces s'y appliquant (sont poids et la force de pression) est nulle (égales en norme).

4b.  $P \ = \ m \times g \ = \rho_{Hg} \times V_{colonne} \times g \ = \rho_{Hg} \times S \times h_{colonne} \times g = \ 13,6.10^{ \ 3} \times 1 \times 0,76 \times 9,81 \ = \ 1,014.10^{ \ 5} N$.

5a.  Si la pression diminue, la force de pression résultante diminue aussi.

Pour compenser cette force, la masse de mercure dans le tube diminuera.

On aura : $\Delta F_{pression} \ = \Delta \left( Poids \right )$.

Soit : $\Delta P \times S \ = \ \Delta m \times g$

$\Leftrightarrow \ \ \Delta P \times S \ = \ \rho \times \Delta h \times S \times g$.

$\Leftrightarrow \ \ \Delta h  \ = \ \dfrac{ \Delta P}{\rho \times g}$.

$\Leftrightarrow \ \ \Delta h  \ = \ \dfrac{ 10.10^{ \ 2}}{13,6.10^{ \ 3} \times 9,81} \ = \ 7,5.10^{ \ -3} \ m \ = \ 7,5 \ mm$.

5b.  En utilisant un fluide moins dense, la hauteur aurait été plus importante.

Pour de l'eau, par exemple, on aurait ontenu une variation de hauteur de $10 \ cm$, le tube serait vide.

Exercice 32 P215 : Mélange de deux liquides.

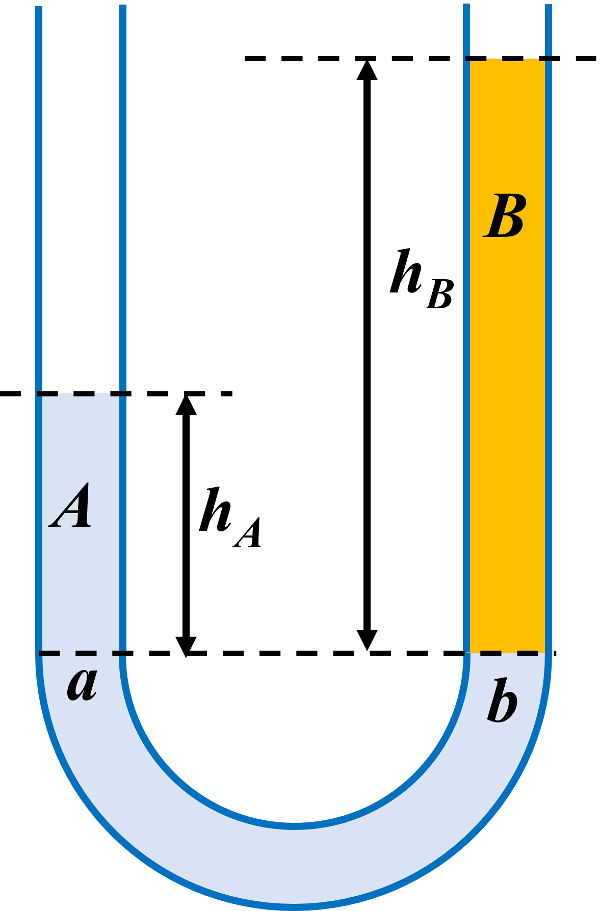
1.  Au niveau de chaque liquide, la pression est égale à la pression atmosphérique $P_{atm}$.

2a.  $P_a + \rho_{eau} \times g \times h_a \ = P_{atm}$.

2b.  $P_b + \rho_{huile} \times g \times h_b \ = P_{atm}$.

3a.  Les poins $a$ et $b$ étant au sein du même liquide (eau), au même niveau $P_a \ = \ P_b \ = P_{atm}$.

3b.  On a donc : $ \rho_{huile} \times g \times h_b \ = \ \rho_{eau} \times g \times h_a $.

4a.  $V_{huile} \ = \ \dfrac{\pi .d^2.h_B}{4} \ \ \Leftrightarrow \ \ h_B \ = \ \dfrac{4\times V_{huile}}{\pi .d^2}$.

4b.  $\rho_{huile} \times g \times h_b \ =  \ \rho_{eau} \times g \times h_a \ \ \Leftrightarrow \ \ \rho_{huile} \times g \times \dfrac{4\times V_{huile}}{\pi .d^2 }\ = \ \rho_{eau} \times g \times h_a $

$ \Leftrightarrow \ \ h_a \ = \ \dfrac{4. \rho_{huile} .V_{huile}}{\pi . d^2. \rho_{eau}}$

$$\Delta h \ = \ h_b - h_a $$
$$ \Leftrightarrow \Delta h \ = \ \dfrac{4\times V_{huile}}{\pi .d^2} - \dfrac{4. \rho_{huile} .V_{huile}}{\pi . d^2. \rho_{eau}} \ $$
$$\Leftrightarrow \Delta h \ = \ \dfrac{4\times V_{huile}}{\pi .d^2} \left ( 1- \dfrac{\rho _{huile}}{\rho _{eau}} \right ) \ = \ 2,5 \ cm$$

Exercice 34 P215 : Principe de la perfusion.

1.

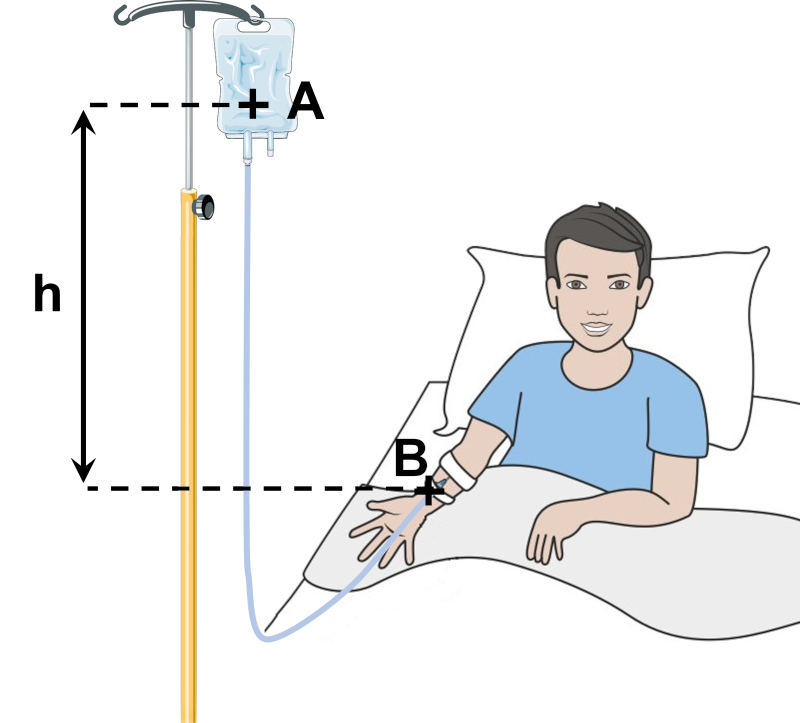Loi de la statique entre les points A et B : $p_A \ + \ \rho \times g \times z_A \ = p_B \ + \ \rho_{eau} \times g \times z_B$ $\Leftrightarrow \ p_B \ - \ p_A \ = \rho_{eau} \times g \times z_A \ - \ \rho \times g \times z_B$ $\Leftrightarrow p_B \ - \ p_A \ = \rho_{eau} \times g \times \left ( z_A - z_B \right )$ $\Leftrightarrow p_B \ - \ p_A \ = \rho_{eau} \times g \times h$

2a.La tension $T$ correspond à la différence de pression $p_A-p_B \ = p_{sang} - p_{atm}$.

$T \ = p_B \ - \ p_A \ = \rho_{eau} \times g \times h$

2b.Pour $p_A=p_{atm}$ et $p_B=p_{sang}$, on a alors : $T \ = p_B \ - \ p_A \ = \rho_{eau} \times g \times h$

Soit : $h \ = \dfrac{T}{\rho_{eau} \times g} \ = \ \dfrac{10,8.10^{ \ 3}}{1,03.10^{ \ 3} \times 9,81} \ = \ 1,06 \ m$

4a.La tension $T$ correspond à la différence de pression $p_{sang} \ = \ T + p_{atm} \ = 10,8.10^{  \ 3} + 1,013.10^{ \ 5} = 1,12.10^{ \ 5} \ Pa$.

4b.Si la poche n'est pas à une hauteur suffisante, $p_B < p_{sang}$. Un retour de sang peut se produire.

5.$T \ = \ \dfrac{12+8}{2} = 10 \ cm \ Hg = 100 mm \ Hg \ = \ 1,33.10^{ \ 4} \ Pa$.

Pour $T \ = \ 13,3.10^{ \ 3} \ Pa$, on a : $h \ = \dfrac{13,3.10^{ \ 3}}{1,0.310^{ \ 3} \times 9,81} = 1,31 \ m$.

Exercice 39 P217 : Voyage à New York.

Loi de la statique des fluides : $\Delta P= \rho \times g \times \Delta z$

Soit : $\Delta z= \dfrac{\Delta P}{ \rho \times g}$

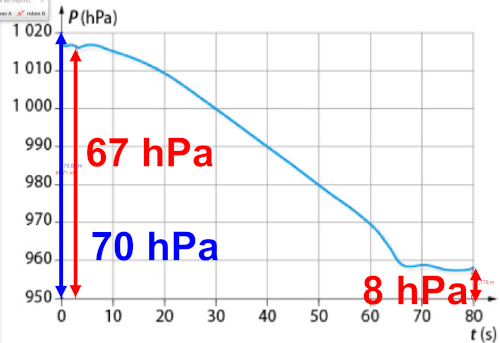A l'aid du graphique, on mesure une différence de pression : $\Delta P = 67-8= 59 \ hPa$

On considère que l'air est composé à 80% de diazote $N_2$ et à 20% de dioxygène $O_2$.

Sa masse molaire est : $M_{air}=0,8 \times 14,0 \times 2 + 0,8 \times 16,0 \times 2 = 28,8 \ g.mol^{ \ -1}$

La valeur de la température est : $T = 273 + 17 = 290 \ K$

En considérant que la masse volumique de l'air reste consante tout au long de la montée, on clacule : $\rho = \dfrac{1017.10^{ \ 2} \times 28,8.10^{ \ -3}}{8,31 \times 290} \ = 1,22 kg.m^{ \ -3}$

On en déduit une différence de hauteur : $\Delta z = \dfrac{\Delta P}{\rho \times g} \ = \dfrac{57.10^{ \ 2}}{9,81 \times 1,22} \ = 478 \ m$

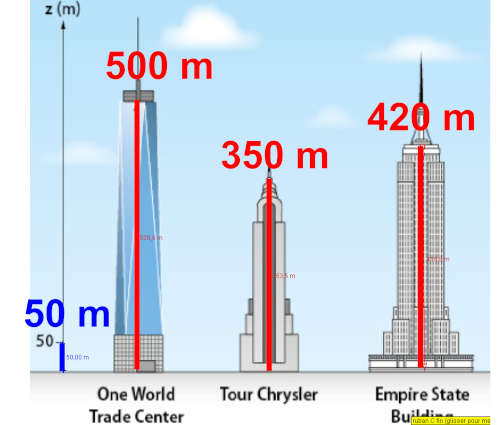En utilsant le schéma donné, on en déduit que Gérard a visitéle le World Trade Center.