Mouvement d'un système

Exercice 9 P231 : Définitions.

1. $\overrightarrow {v_5} \ = \ \dfrac{\overrightarrow {M_5M_6}}{\Delta t}$

2. $\Delta \overrightarrow {v_5} \ = \ \dfrac{\overrightarrow {v_6} - \overrightarrow {v_5}}{\Delta t}$.

Exercice 10 P231 : Phrases à compléter.

Exercice 11 P231 : Soustraire deux vecteurs.

1. $\Delta \overrightarrow {v_3} \ = \ \overrightarrow {v_4} \ - \ \overrightarrow {v_2}$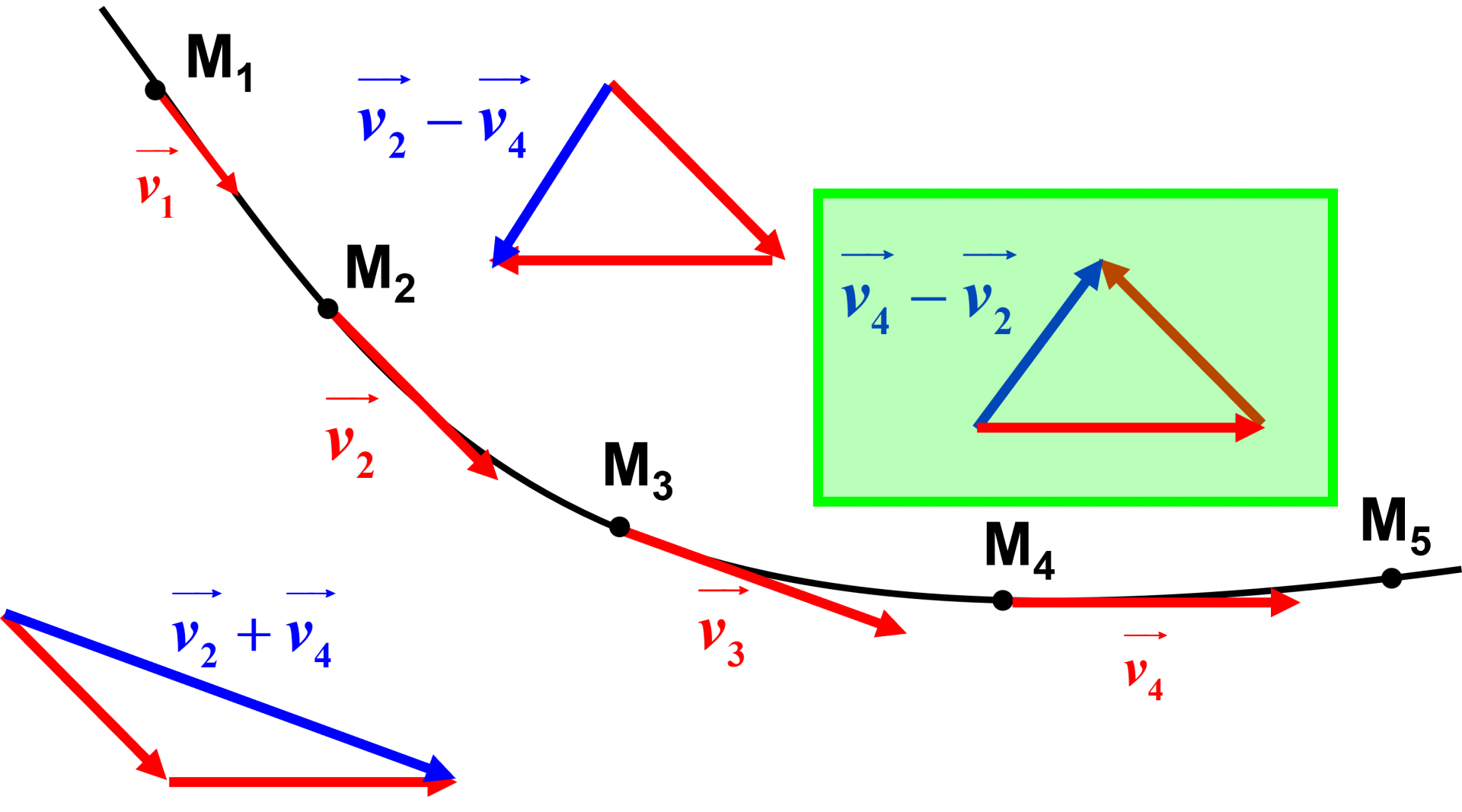

2.

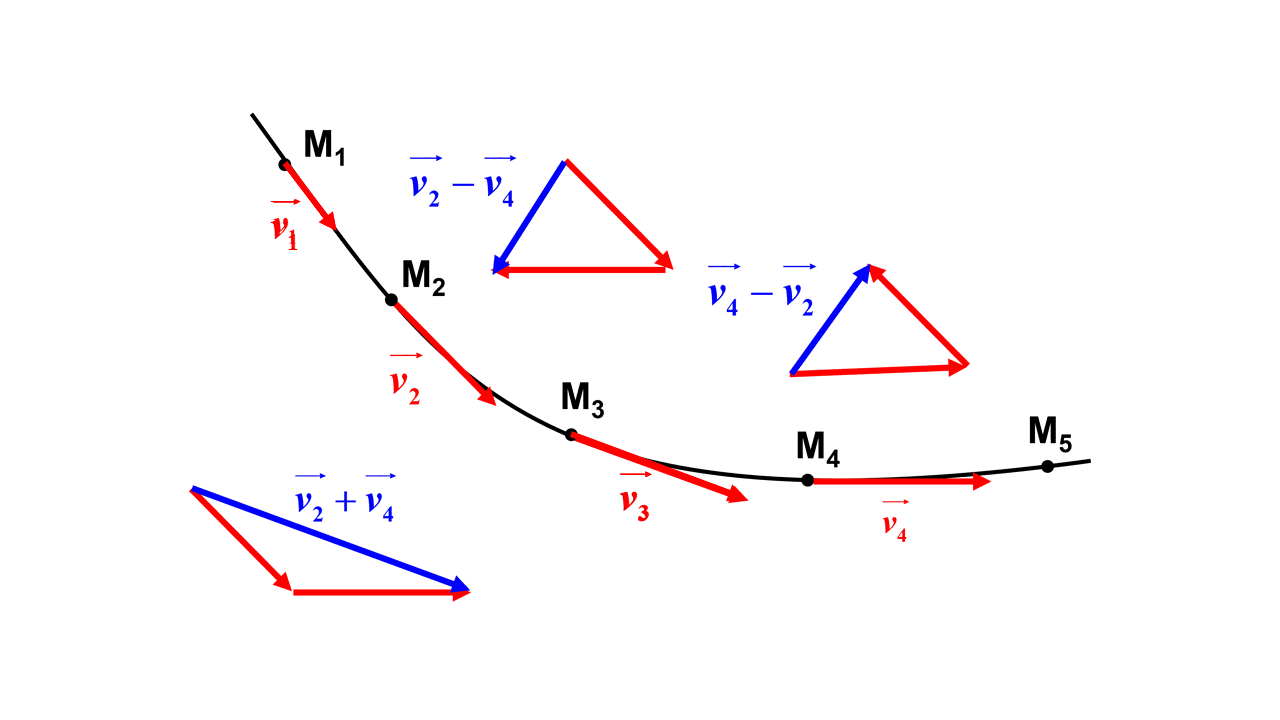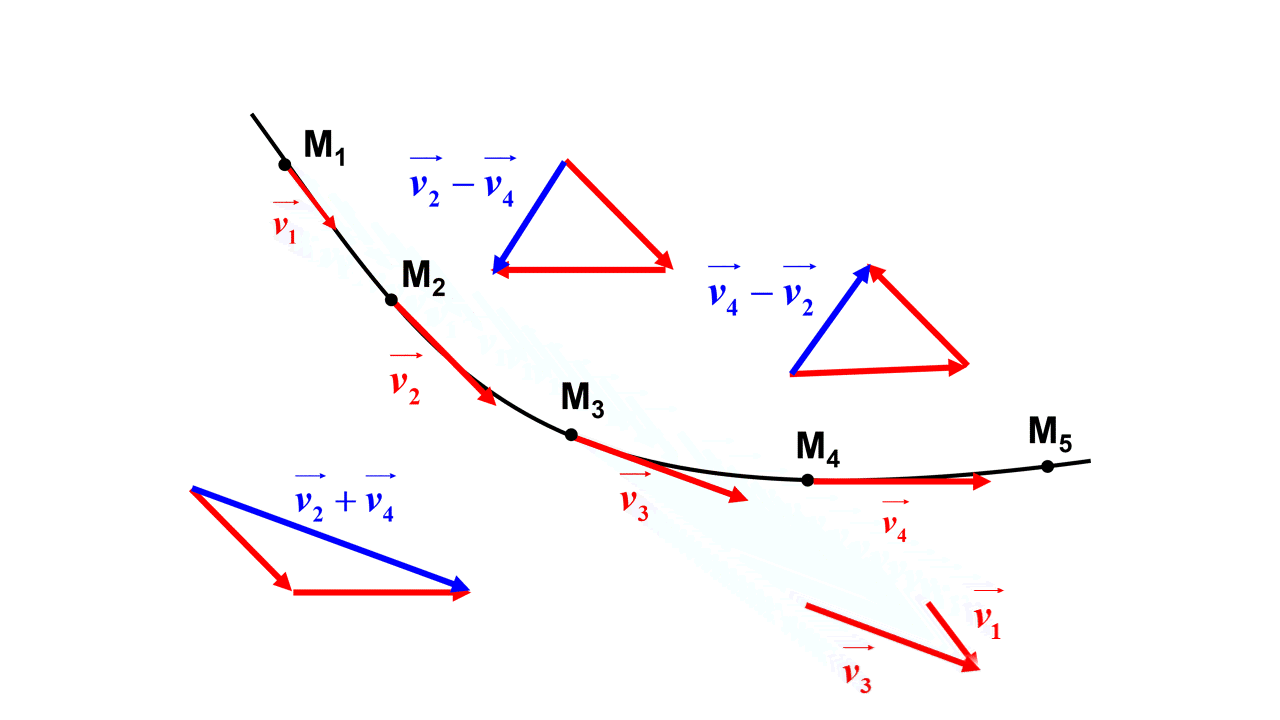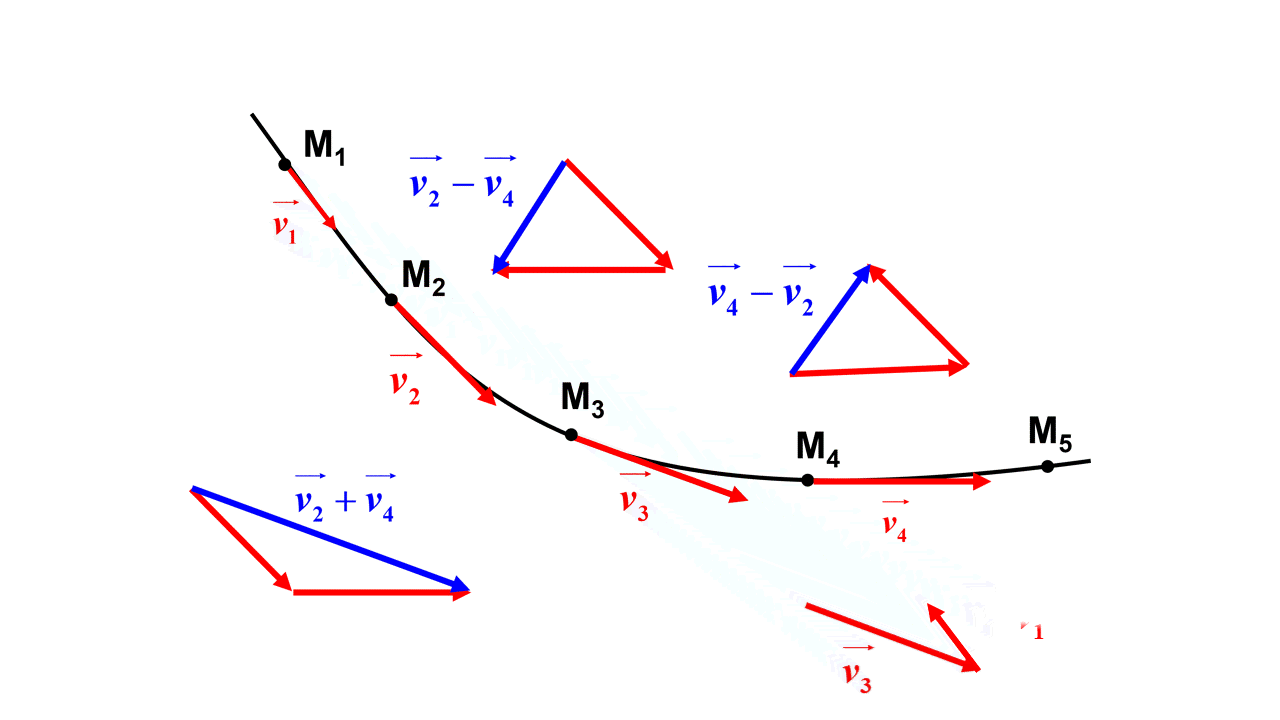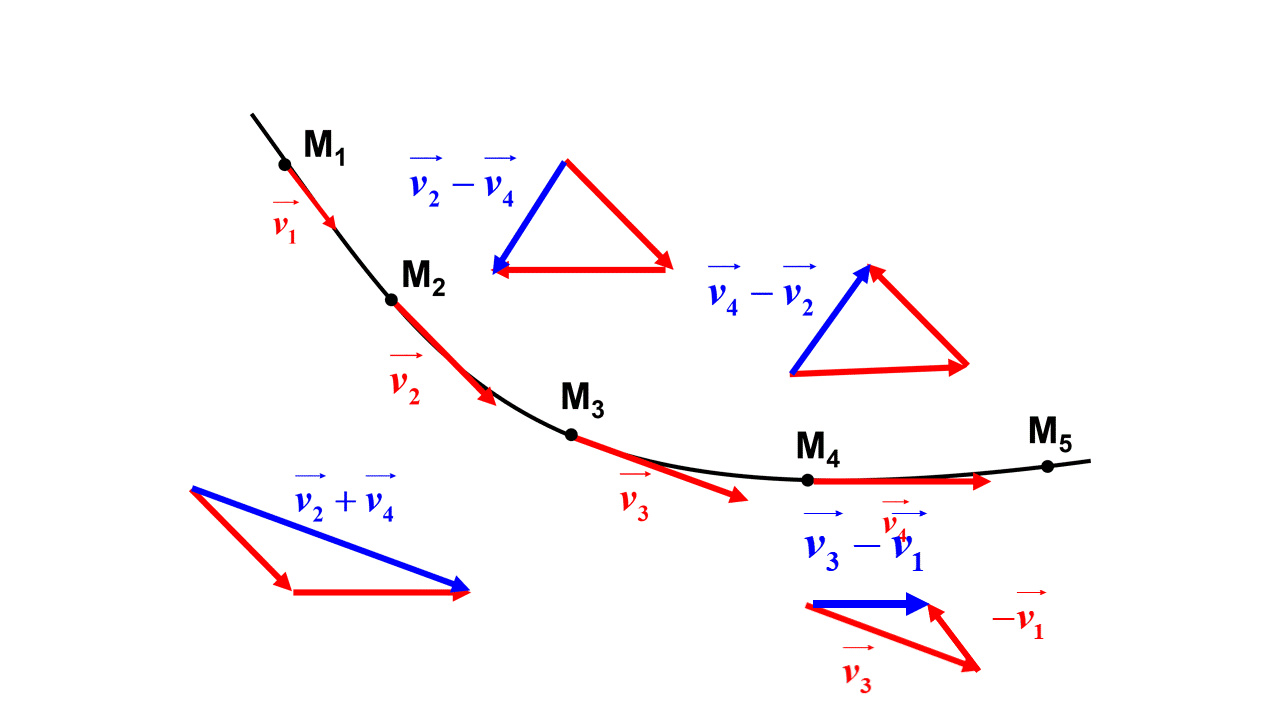
3. Pour pouvoir tracer le vecteur variation de vitesse au point $M_4$, $\Delta \overrightarrow {v_4} \ = \ \overrightarrow {v_5} \ - \ \overrightarrow {v_3}$, il faudrait avoir le vecteur vitesse $\Delta \overrightarrow {v_5}$. On ne peut donc pas tracer le vecteur variation de vitesse au point $M_4$.

Exercice 13 P231 : Accéléré ou retardé ?

1, 2.

Pour l'enregistrement 1 :

La distance parcourue pendant un même intervalle de temps $\Delta t \ = \ 40 \ ms$, la distance est la même. Le mouvement s'effectue le long d'une droite. Il s'agit d'un mouvement rectiligne uniforme.

Le vecteur vitesse a la direction et le sens de l'axe $\left ( Ox \right )$

Pour l'enregistrement 2 :

La distance parcourue pendant un même intervalle de temps $\Delta t \ = \ 40 \ ms$, la distance augmente. Le mouvement s'effectue le long d'une droite. Il s'agit d'un mouvement rectiligne accéléré.

Le vecteur vitesse a la direction et le sens de l'axe $\left ( Ox \right )$.

Pour l'enregistrement 3 :

La distance parcourue pendant un même intervalle de temps $\Delta t \ = \ 40 \ ms$, la distance diminue. Le mouvement s'effectue le long d'une droite. Il s'agit d'un mouvement rectiligne ralenti.

Le vecteur vitesse a la direction et le sens de l'axe $\left ( Ox \right )$

3. En utilisant le logiciel "Tracker", et en calibrant la distance, nous allons pouvoir déterminer les distances parcourues entre le point 5 et le point 6 pour chaque enregistrement.

Enregistrement 1 : $v_5 \ = \ \dfrac{M_5M_6}{\Delta t} \ = \ \dfrac{0,297}{40.10^{ \ -3}} \ = \ 7,43 \ m.s^{ \ -1}$

Enregistrement 2 :$v_5 \ = \ \dfrac{M_5M_6}{\Delta t} \ = \ \dfrac{0,274}{40.10^{ \ -3}} \ = \ 6,85 \ m.s^{ \ -1}$

Enregistrement 3 :$v_5 \ = \ \dfrac{M_5M_6}{\Delta t} \ = \ \dfrac{0,267}{40.10^{ \ -3}} \ = \ 6,68 \ m.s^{ \ -1}$

Exercice 14 P231 : Grande roue.

1.La distance parcourue pendent le même intervalle de temps semble la même entre chaque point, ce qui implique que la vitesse est constante. Le vacteur vitesse ne varie pas en norme.

La trajectoire est un cercle.

Nous sommes dans le cas d'un mouvement circulaire uniforme.

Le vecteur-vitesse est tangent à la trajectoire. Sa direction et son sens varie tout au long du déplacement sur la tangente au cercle en chaque point.

2,3,4.

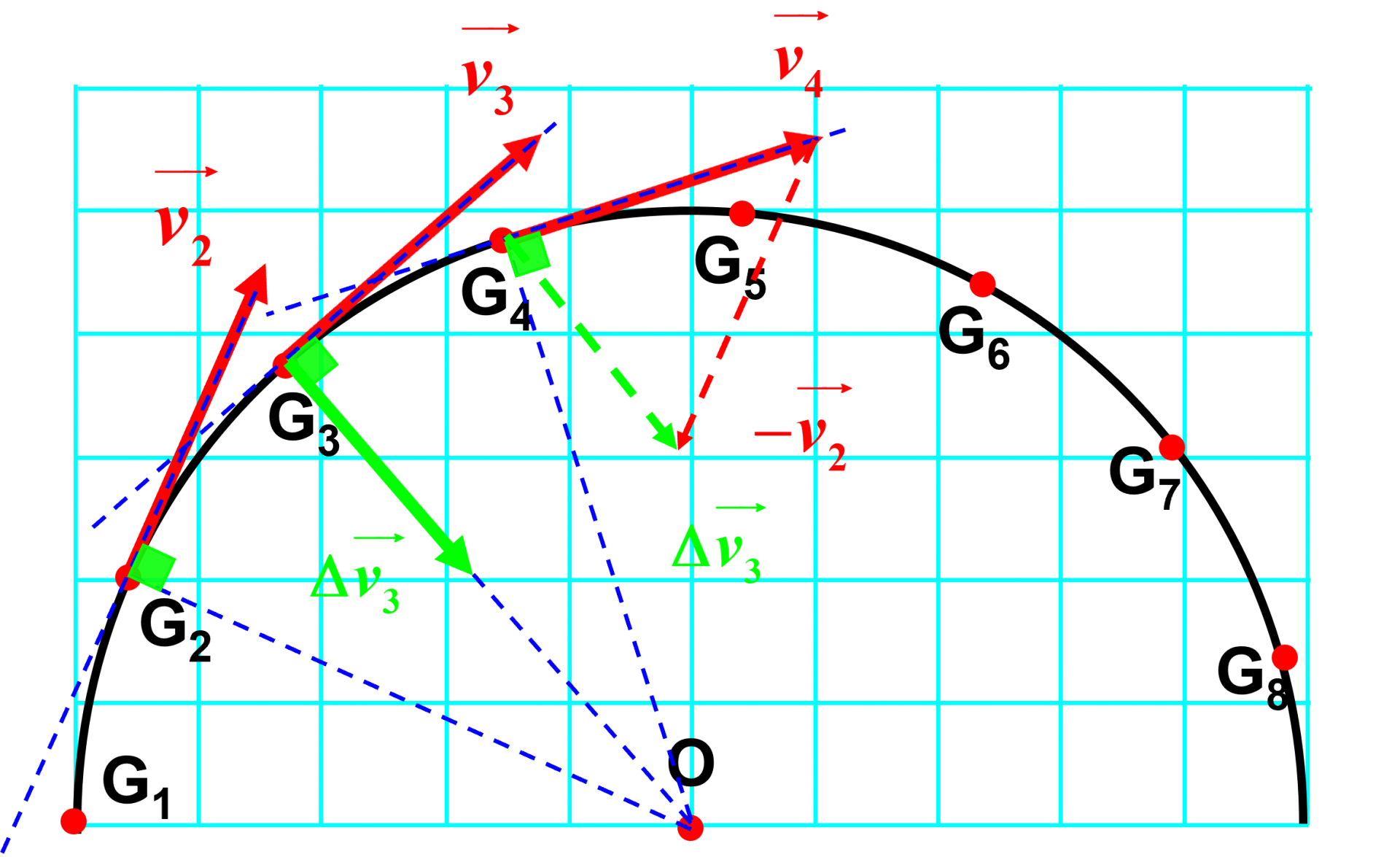
Le vecteur variation de vitesse $\Delta \overrightarrow {v_3} \ = \ \overrightarrow{v_4} \ - \ \overrightarrow{v_2}$ est centripète au point $M_2$.

Exercice 18 P232 : Somme de forces.

1. Si la somme des forces était nulle, le mouvement du système serait rectiligne (et uniforme). La trajectoire n'étant pas restiligne, la somme des forces n'est pas nulle.

2.

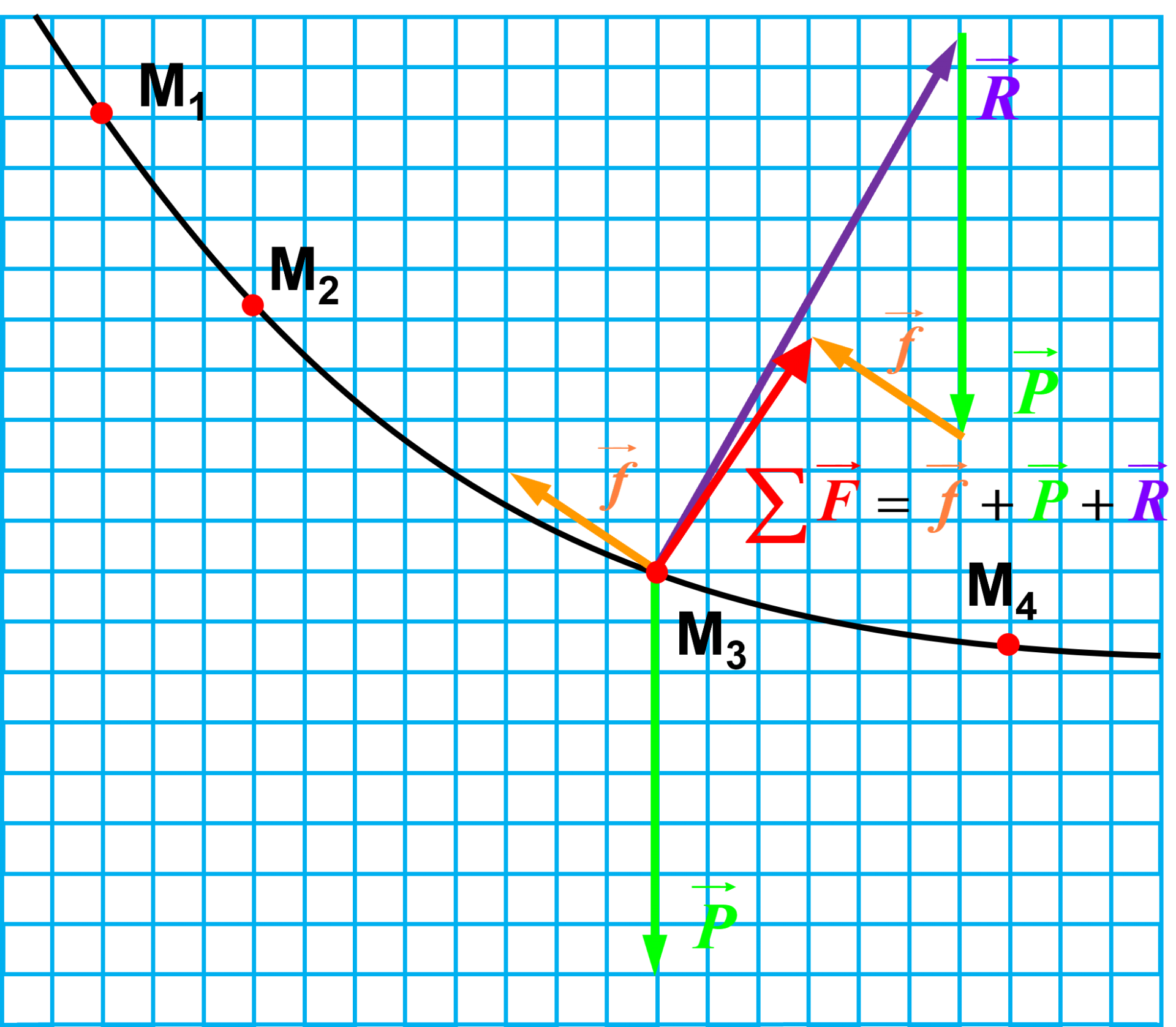
3. $\Sigma \overrightarrow F \ = \ m \times \dfrac{\overrightarrow{\Delta v}}{dt}$

Les vecteur $\Sigma \overrightarrow F$ et $ \Delta \overrightarrow v$ sont de même sens.

Exercice 20 P233 : Somme de forces.

1. La bille se met en mouvement car elle est soumise à son poids $\overrightarrow P$ Comme $\Sigma \overrightarrow F \ = \ m \times \dfrac{\overrightarrow{\Delta v}}{dt}$, la vitesse variera. 2. La masse $m$ ne variant pas, la variation de vitesse $\dfrac {\overrightarrow{\Delta v}}{dt} \ = \ \dfrac{1}{m} \overrightarrow P$ est consante.

Exercice 27 P234 : Intensité de la pesanteur.

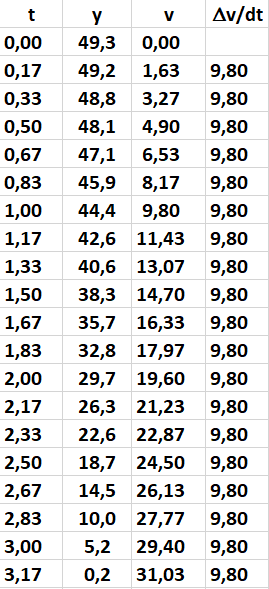
1,2. Après avoir pointer la vidéo dans tracker, avec 6 images par senconde $\left ( \Delta t \ = \ 0,167 \ s \right )$, on obtient les mesures et résultats suivants :

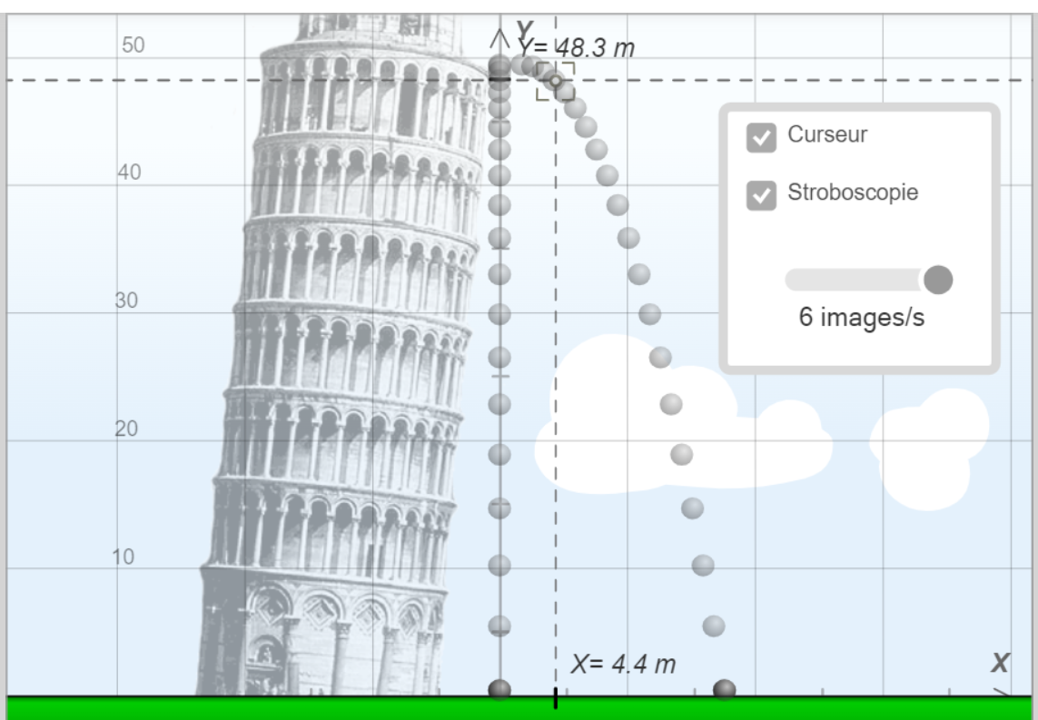Position verticale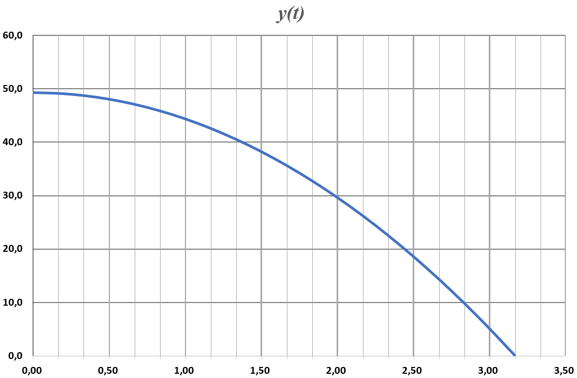
Vitesse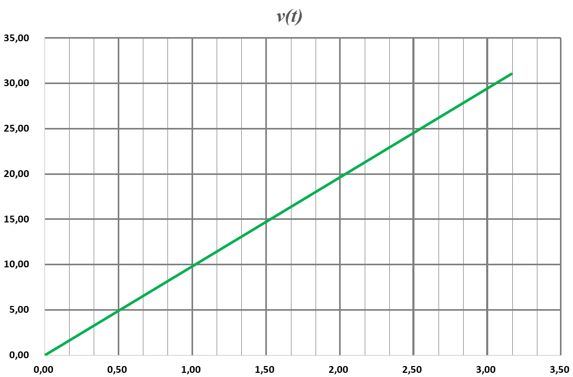
$\dfrac {\Delta v}{dt}$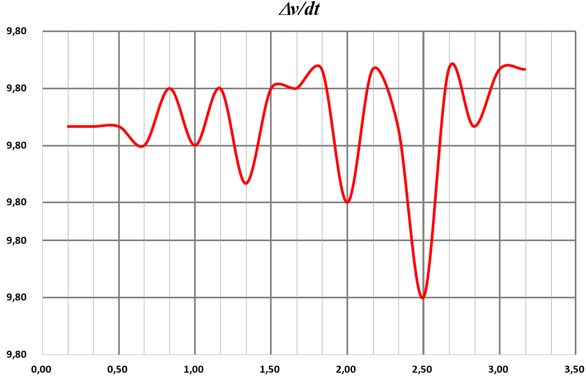

La variation de vitesse $\dfrac{\Delta v}{dt}$ est constante est a pour valeur : $\dfrac{\Delta v}{dt} \ = \ 9,8 \ m.s^{ \ -2}$

Dans le cas présent : $ \dfrac{\Delta v}{dt} = \ \dfrac{1}{m } \times \overrightarrow P \ = \ 9,8 \ m.s^{ \ -2} \ = g$

Exercice 29 P235 : Billard.

1. Au moment de l'impact, les forces s'exerçant sur la bille sont :

Son poids $\overrightarrow P$, vertical, vers le bas, s'appilquant au centre de gravité de la bille, de valeur $P \ = \ mg$.

La réaction de la table $\overrightarrow R$, verticale vers le haut, s'appliquant au point de contact de la bille et de la table, de valeur $R \ = \ P$.

La force $\overrightarrow F$ exercée par la queue, horizontale, au point d'impact.

NB : $\overrightarrow P \ + \ \overrightarrow R \ = \ \overrightarrow 0$.

En effet, avant l'impact, la bille est immobile sur la table.

2. A l'instant de l'impact de la queue sur la bille : $\Sigma \overrightarrow {f_{ext}} = \ \overrightarrow P \ + \ \overrightarrow R \ + \ \overrightarrow F \ = \ \overrightarrow F $

Alors : $\Sigma \overrightarrow F \ = \ m \times \dfrac{\overrightarrow{\Delta v}}{dt}$, il y a une variation de la vitesse, elle se met en mouvement.

Puis, les seules forces s'appliquant étant de poids $\overrightarrow P$ et la réaction $\overrightarrow R$. Leur somme étant nulle, on a : $\Sigma \overrightarrow F \ = \ \overrightarrow 0 \ m \times \dfrac{\overrightarrow{\Delta v}}{dt}$, la variation de vitesse est constante. Le mouvement est rectiligne uniforme.

3. La bille subit une force de frottement de la part du tapis. Cette force est opposée au déplacement de la bille. Elle finira par s'arrêter.

Exercice 34 P237 : Glisser sans frottement.

1. Le solide est à l'équilibre. La somme des forces s'y appliquant est nulle.

2.

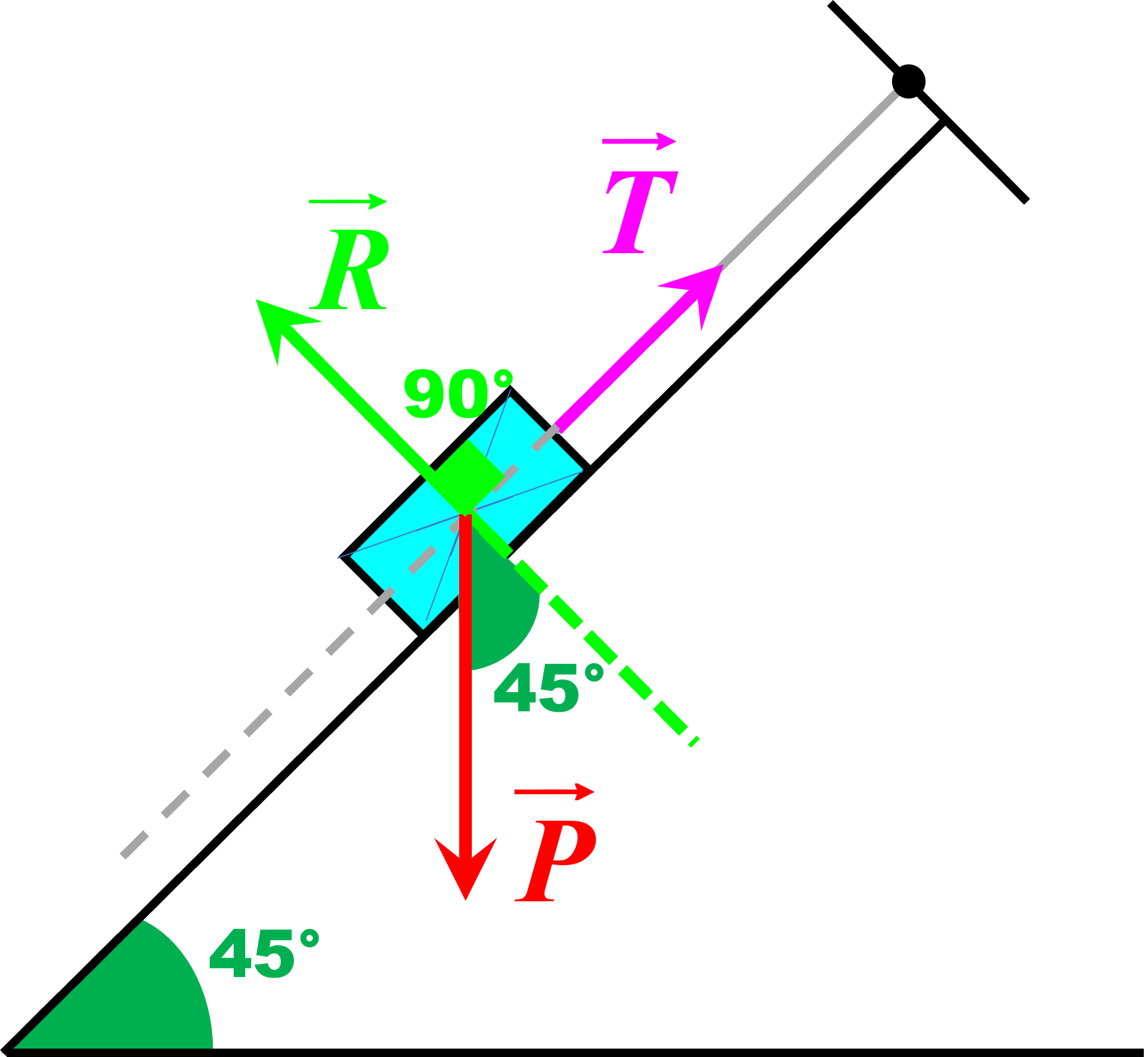
3. $P \ = \ m \times g \ = \ 0,250 \times 9,8 \ = \ 2,5 \ N$.

4.

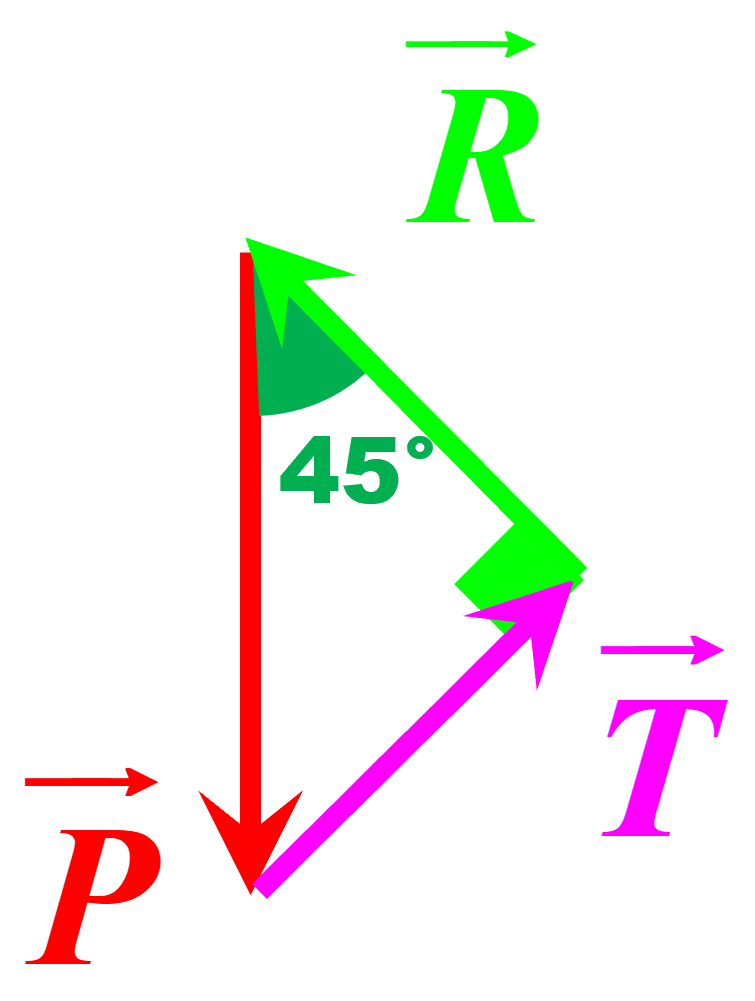
$cos(45°) \ = \ \dfrac{R}{P} \ \Leftrightarrow \ \ R \ = cos(45°) \times P \ = \ 1,7 \ N $

$sin(45°) \ = \ \dfrac{T}{P} \ \Leftrightarrow \ \ T \ = sin(45°) \times P \ = \ 1,7 \ N $

5. Dès que le fil se rompt, les seules forces s'exerçant sur le solide sont : son poids $\overrightarrow P$ et la réaction du plan $\overrightarrow R$.

Précédemment, on avait : $\overrightarrow P + \overrightarrow R + \overrightarrow T \ = \ \overrightarrow 0$

On a donc : $\overrightarrow P \ + \ \overrightarrow R \ = \ - \ \overrightarrow T$

6. Comme $\overrightarrow P + \overrightarrow T \ = \ - \overrightarrow T \ = \ \ m \times \dfrac {\Delta \overrightarrow v}{\Delta t}$, on a :

$\left | \left | \overrightarrow T \right | \right | \ = \ m \times \dfrac{ \left | \left | \overrightarrow {\Delta v} \right | \right |}{\Delta t}$

Soit : $ \Delta v \ = \ v - 0 \ = \ v \ = \ \dfrac{T}{m} \ = \ \dfrac{1,7}{0,250} \ = \ 6,9 \ m.s^{ \ -1}$

Exercice 35 P237 : Mouvement de la Lune.

1, 2.

3.

$\overrightarrow F \ = \ m_L. \dfrac{\Delta \overrightarrow v}{\Delta t}$. Donc : $\Delta \overrightarrow v \ = \ \dfrac{1}{m_L} \overrightarrow F \times \Delta t $

$\Delta v \ = \dfrac{1}{m_L} \times \dfrac{G.m_L.m_T}{d_{TL}^2} \times \Delta t$

$\Leftrightarrow \ \ \Delta v \ = \dfrac{1}{m_L} \times \dfrac{G.m_L.m_T}{d_{TL}^2} \times \Delta t$

$\Leftrightarrow \ \ \Delta v \ = \dfrac{G.m_T}{d_{TL}^2} \times \Delta t$

$\Leftrightarrow \ \ \Delta v \ = \dfrac{6,67.10^{ \ -11} \times 5,97.10^{ \ 24}}{\left (3,84.10^{ \ 8} \right )^2} \times \dfrac {27 \times 86400 + 8 \times 3600}{4}$

$\Delta v \ = \ 1,6.10^{ \ 3 } \ m.s^{ \ -1}$

4. 

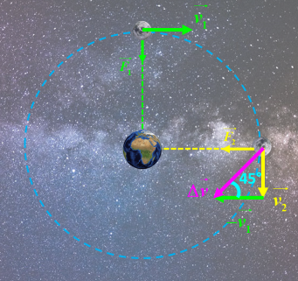
$sin (45) \ = \ \dfrac{v}{\Delta v}$ soit : $v \ = \ \Delta v \times sin 45 \ = \ \dfrac{\Delta v}{\sqrt 2}$

5. $v \ = \ \dfrac{ 1,6.10^{ \ 3}}{\sqrt 2} \ = \ 1,1.10^{ \ 3 } \ m.s^{ \ -1}$. En accord avec les valeurs trouvées sur différents sites.