Ondes mécaniques Exercices
Exercice n°8 P 305 : Notion de retard.

1a.
L’onde se propage le long de la corde dans une seule direction, et un point de la corde ne se déplace que verticalement.
1b.
Horizontalement de M vers M’ (de gauche à droite).
2.
Il faudrait connaître la célérité c de l’onde et la valeur de $\tau$.
Alors, $c \ = \ \dfrac{MM'}{\tau}$ Où $MM'$ est la distance entre les deux points sur la corde.
On a donc :, $MM' \ = \ c \times \tau$.
3a.
$\tau$ représente le temps que l’onde a mis pour parcourir la distance $MM’$. Le point M a subi la déformation à l’instant $t$ et le point M’ à $t \ + \tau$.
3b.
Le point M a subi la déformation à l'instant $t$, le point M' la subit à l'instant $t' \ = \ t + \tau$
3c.
Le point M'subit la déformation « $\tau$ " plus tard ». Il s’agit du RETARD.
3d.
En connaissant la distance $d$ et la célérité $c$ de l'onde on a : $\tau \ = \ \dfrac{d}{c}$.
Exercice n°10 P 305 : Célérité d'une onde le long d'une corde.
1a.
Un point de la corde ne se déplace que verticalement.
1b.
Il s'agit d'une onde mécanique progressive transversale.
2.
3.
La célérité de l'onde est : $c \ = \ \dfrac{64}{165.10^{ \ -3}} \ = \ 388 \ cm^{ \ -1} \ = \ 3,88 m.s^{ \ -1}$ soit : $14 \ km/h$.
Exercice n°11 P 305 : A la pêche.

1.
La feuille n'est pas transportée par l'onde. Elle reste à la même distance du bouchon. Seule sa position verticale varie avec l'onde.
2.
La célérité de l'onde est : $c \ = \ \dfrac{20}{2,5} \ = \ 8,0 \ cm.s^{ \ -1}$.
Exercice n°13 P 305 : Ondes mécaniques.
 |
 |
1.
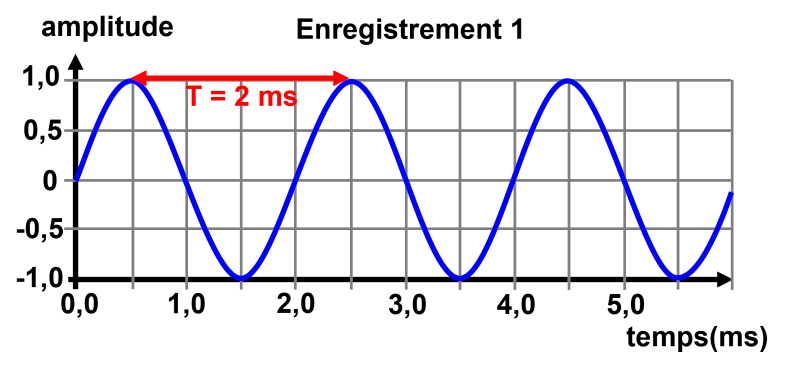
Dans les deux cas, les ondes étant sonores, il s'agit d'ondes mécaniques. Sur l'enregistrement 1, l'onde est sinusoïdale.
2a.
Les périodes ne sont pas les mêmes.
Pour le premier enregistrement, on mesure une période $T_1 \ = \ 2 \ ms$.
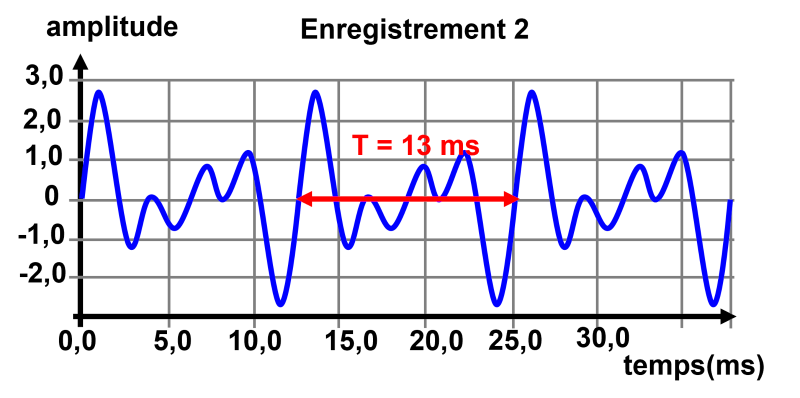
Pour le premier enregistrement, on mesure une période $T_2 \ = \ 13 \ ms$.
2b.
On en déduit : $f_1 \ = \ \dfrac{1}{2.10^{ \ -3}} \ = \ 500 \ Hz$ et $f_2 \ = \ \dfrac{1}{13.10^{ \ -3}} \ = \ 77 \ Hz$ .
NB :
Connaissant la célérité du son dans l'air $c_{son} \ = \ 340 \ m/s$, on peut aussi déterminer la longueur $\color{red}{\lambda \ = \ c_{son} \times T}$ d'onde de chaque signal.
$\lambda_1 \ = \ 340 \times 2.10^{ \ -3} \ = \ 0,68 \ m$ et $\lambda_2 \ = \ 340 \times 13.10^{ \ -3} \ = \ 4,42 \ m$ .
Exercice n°14 P 306 : Emetteur à ultrasons.
1.
Une onde sonore est une onde mécanique longitudinale. Dans le cas proposée, elle est périodique et sinusoïdale.
2a.
Pour être le plus précis, on mesure la durée correspondant à un maximum de périodes sur l'intervalle de temps le plus long possible.
2a.
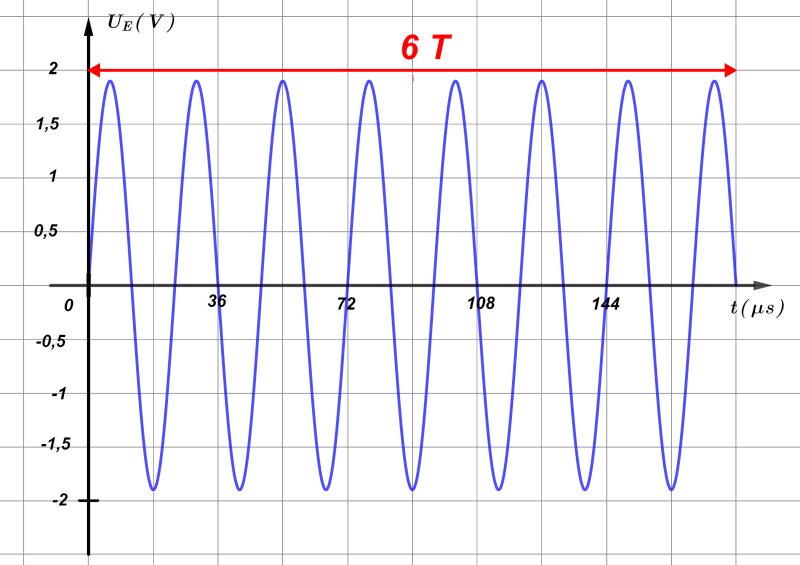
On mesure une durée de $144 \ \mu s$ pour 6 périodes.
On en déduit : $T \ = \ \frac{144}{6} \ = \ 24 \mu s$
2b.
Au vu de l'épaisseur du trait sur le graphique, on peut dire que : $23 \mu s \leq T \leq 25 \mu s$.
On écrit : $T \ = \ 24 \pm 1 \mu s$.
3.
La fréquence calculée est : $f \ = \ \dfrac{1}{24.10^{ \ -6}} \ = \ 42 \ kHz$, ce qui corrspond bien à la fréquence d'un ultrason.
Exercice n°15 P 306 : Son émis par un diapason.
1.
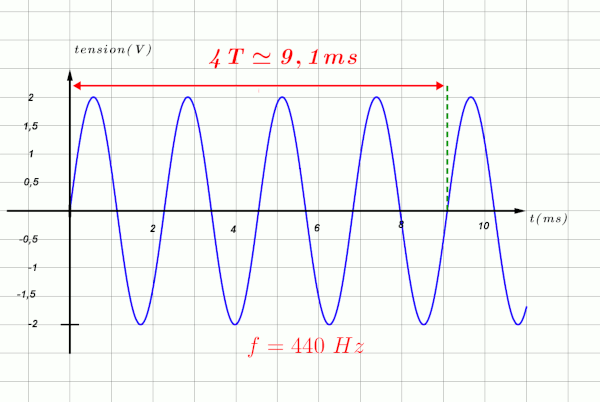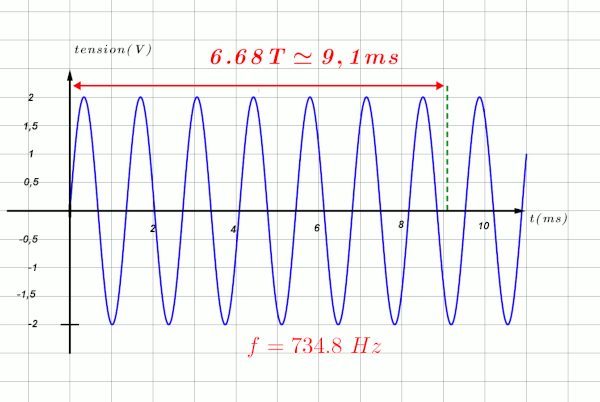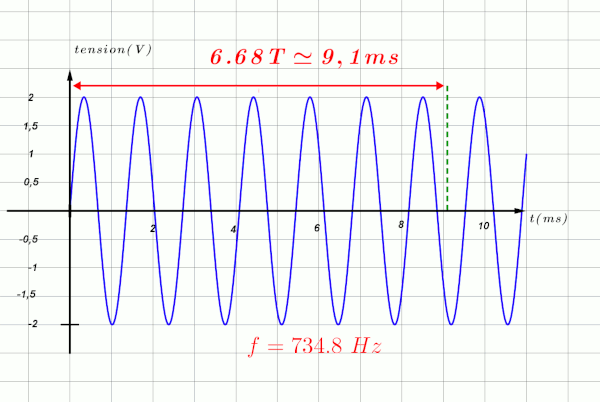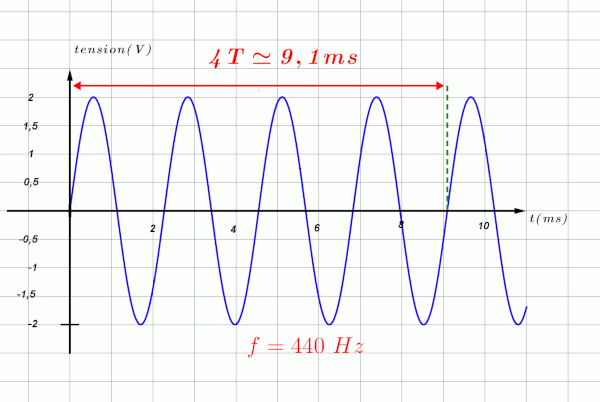
440 Hz correspond à la fréquence du son émis par le diapason.
2a.
On mesure le temps correspondant à un nombre maximum de périodes.
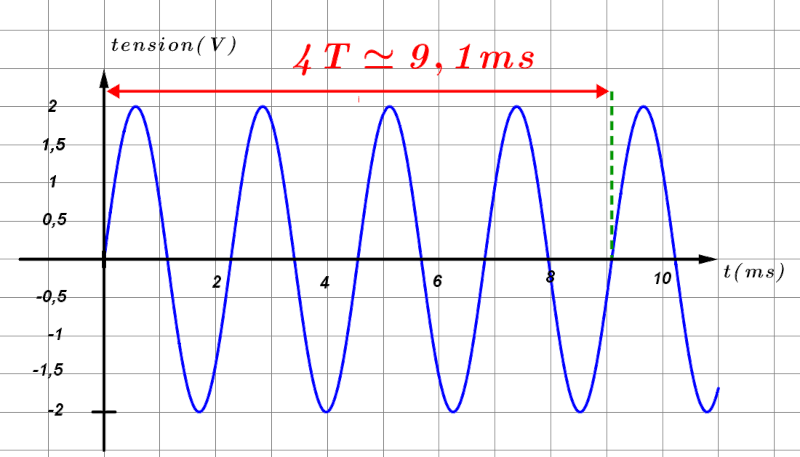
Pour 4 périodes, on mesure une durée de $\Delta t \ = \ 9,1 \ ms$ On en déduit une période : $T \ = \ \dfrac{9,1}{4} \ = 2,28 \ ms$.
2b.
On en déduit une fréquence $f \ = \ \dfrac{1}{2,28.10^{ \ -3}} \ = \ 440 \ Hz$. Ce qui correspond à la fréquence proposée.
3.
3a.
$Leftrightarrow T \ = \ \dfrac{1}{f}$, si la fréquence double, la période sera divisée par 2.
Sur un même intervalle de temps donné, le nombre de périodes augmente, il est multiplié par 2.
3b.
$T_2 \ = \ \dfrac{9,1}{8} \ = 1,24 \ ms$
Exercice n°17 P 307 : Longueur d'onde.
1.
La longueur d'onde $\lambda$ correspond à la période SPATIALE de l'onde.
2.
$\lambda \ = \ \dfrac{c}{f}$.
Exercice n°18 P 307 : Longueur d'onde et fréquence.
1a.
On en déduit : $\lambda_1 \ = \ \dfrac{7}{7} \ = \ 1 \ cm$.
1b.
La célérité est : $v_1 \ = \lambda_1 \times f_1 \ = \ 1 \times 8,0 \ = \ 8 \ cm/s$.
2.
En procédant de la même façon que précédemment, on mesure une longueur d'onde $\lambda_2 \ = \ 0,77 \ cm$.
La célérité est : $v_2 \ = \lambda_2 \times f_2 \ = \ 0,77 \times 17 \ = \ 13 \ cm/s$.
Exercice n°21 P 308 : Jeter l'ancre.
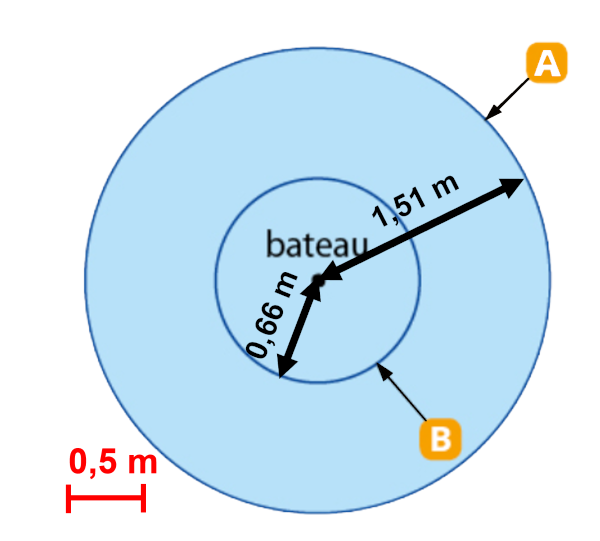
1.
Le front A correspond à la position du front d'onde à l'instant $t_1$.
Le front B correspond à la position du front d'onde à l'instant $t_2$.
2.
Le front d'onde a parcouru la distance $d \ = \ 1,51-0,66 \ = \ 0,85 \ m$ pendant la durée $\Delta t \ = \ t_2 - t_1 \ = \ 3,0 \ s$.
La célérité de l'onde est : $v \ = \ \dfrac{d}{\Delta t} \ = \ \dfrac{0,85}{3,0} \ = \ 2,8 \ m.s^{ \ -1}$.
Exercice n°23 P 309 : Cuve à onde et lame vibrante.
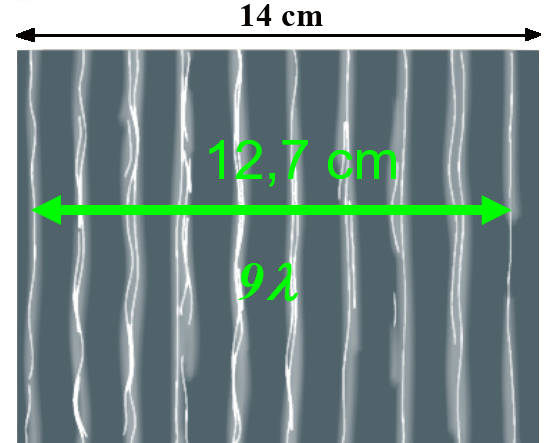
En utilisant l'échelle du document, on mesure une distance de $12,7 \ cm$ pour 9 longueurs d'onde : $9 \lambda \ = \ 12,7 \ cm$
On en déduit une célérité : $c \ = \ \lambda \times f \ = \ \dfrac{12,7}{9} \times 23 \ = \ 32,5 \ cm.s^{ \ -1}$
Exercice n°27 P 311 : Emission et réception d'un son.
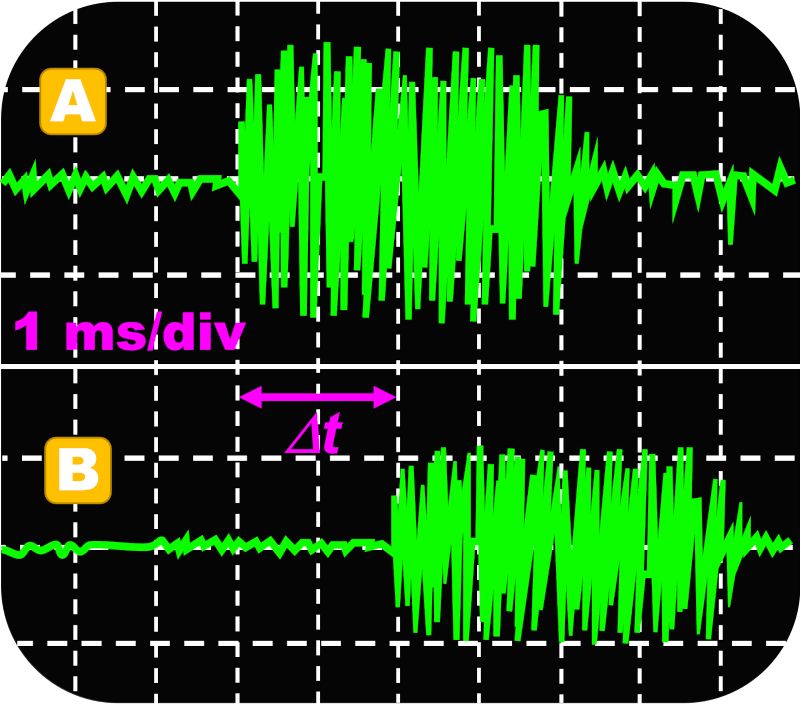
1.
Le son est dû à des compressions se progageant dans l'air.
2a.
Le signal correspondant à l'émetteur est celui qui a la plus grande amplitude. En effet, l'amplitude diminue au cours de la propagation.
De plus, sur le graphique, on constate que le signal A débute avant le signal B.
2b.
On mesure sur l'oscillogramme, un retard $\Delta t \ = \ 2 \times 1,0 \ = \ 2 \ ms$
3a.
La célérité du son dans l'air étant $c \ = \ 340 \ m.s^{ \ -1}$, la distance parcourue par l'onde est : $d \ = \ c \times \Delta t \ = \ 340 \times 2.10^{ \ -3} \ = \ 0,68 \ m$
3b.
Application, déterminer la distance entre un mobile et un obstacle.
Exercice n°30 P 308 : Cuve à ondes.
1a.
La longueur d'onde est la période spatiale.
1b.
Mesurer la distance entre deux points A et B dans le même état de vibration (maximum ou minimum) et rapporter cette distance aux nombre de points dans le même état situés entre ces deux points.
1c.

On mesure : $6 \lambda \ = \ 6,83 \ cm \ \Leftrightarrow \lambda \ = \ 1,14 \ cm$
2.

Après une demi-période, les maxima se sont déplacés d'une demi-longueur d'onde.

Ajouter un commentaire
