Titrage colorimétrique
Exercice n°8 : Masse molaire atomique du carbone.
1. Dans une mole d'atomes de carbone (comme dans une mole de n'importe quoi), il y a $N_a \ = \ 6,02.10^{ \ 23}$ atomes de carbone.
2. La masse molaire atomique du carbone est donc : $M(C) = m_C \times N_a \ = \ 12,0 \ g.mol^{ \ -1}$.
3. On retrouve cette valeur dans la classification périodique des éléments.
Exercice n°10 : Utilisation du tableau périodique.
Après recherche dans la classification périodique des éléments, on trouve :
M(C) = 12,0 g/mol ; M(H) = 1,0 g/mol ; M(O) = 16,0 g/mol ; M(N) = 14,0 g/mol et M(F) = 19,0 g/mol.
| Entité chimique | Formule brute | Masse molaire (en $g.mol^{ \ -1}$ |
| Méthane | $CH_4$ | $M(CH_4) \ = \ 1 \times 12,0 \ + \ 4 \times 1,0 \ = \ 16,0 \ g.mol^{ \ -1}$ |
| Ion fluorure | $F^{ \ -}$ | $M(F^{ \ -}) \ = \ 1 \times 19,0 \ = \ 19,0 \ g.mol^{ \ -1}$ |
| Ethanol | $C_2H_6O$ | $M(C_2H_6O) \ = \ 2 \times 12,0 \ + \ 6 \times 1,0 \ + \ 1 \times 16,0 \ = \ 46,0 \ g.mol^{ \ -1}$ |
| Ammoniac | $NH_3$ | $M(NH_3) \ = \ 1 \times 14,0 \ + \ 3 \times 1,0 \ = \ 17,0 \ g.mol^{ \ -1}$ |
Exercice n°22 : Eau de Dakin.
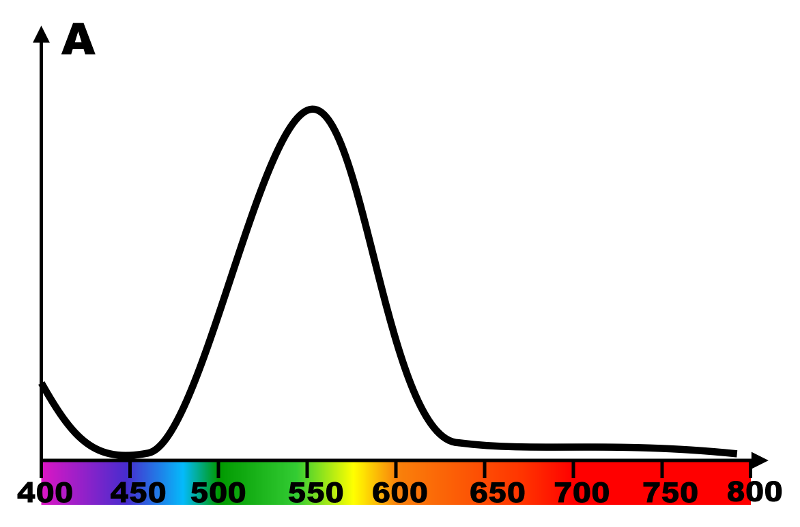
1. L'eau de Dakin apparaissant violet, elle transmet le rouge et le bleu, absorbant le vert.
2.

Bleu : 450 nm ; Vert : 520 nm ; Rouge : 700 nm
3.
Exercice n°23 : Traceur sanguin.
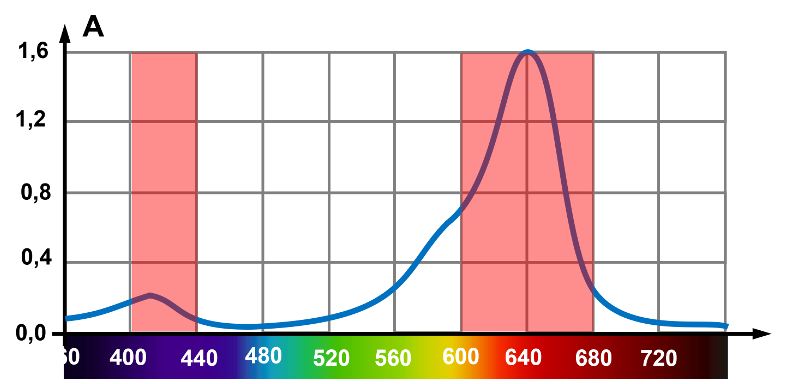
1,2. Les zones d'absorption s'étendent de 400 à 440 nm (bleu), et majoritairement de 600 à 680 nm (rouge). La transmission s'effectue de 440 à 600 nm (vert et jaune).
3. La solution absorbant majoritairement le rouge, par synthèse additive, la solution paraitra cyan.
Exercice n°24 : Préparation d'un dosage.
1. Pour réaliser une dilution, il faut prélever exactement un volume $v$ donné de la solution mère de concentration $C$, à l'aide d'une pipette ou d'une éprouvette. Verser ce prélèvement dans une fiole jaugée de volume $V$ que l'on complète à la jauge. La concentration de la solution obenue sera : $c_f \ = \ \dfrac {v \times C}{V}$.
2. Lors de cette opération, la quantité de matière $n \ = \ C \times V$ prélevée reste la même.
3.
| Solution fille | 1 | 2 | 3 | 4 |
| Volume prélevé $V_{mère}$ (en mL) | 10 | 20 | 30 | 40 |
| Volume final $V_fille$ (en mL) | 50 | 50 | 50 | 50 |
| Concentration finale $c_{fille}$ (en $\mu mol.L^{ \ -1}$ ) | $c_f \ = \ \dfrac {10 \times 34}{50} \ = \ 6,8$ | 13,6 | 20,4 | 27,2 |
2
Exercice n°26 : Dosage par étalonnage.
 |
 |
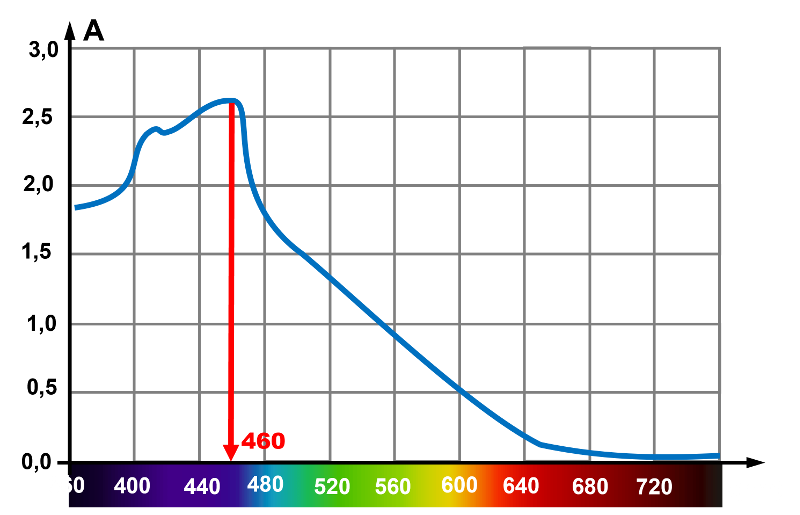
1. Le spectrophotomètre devra être réglé à la longueur d'onde $\lambda \ = \ 460 \ nm$, maximum d'absorbance du produit. Mesurer une grandeur, autant la mesurer à son maximum, puisqu'en diluant, l'absorbance diminuera.
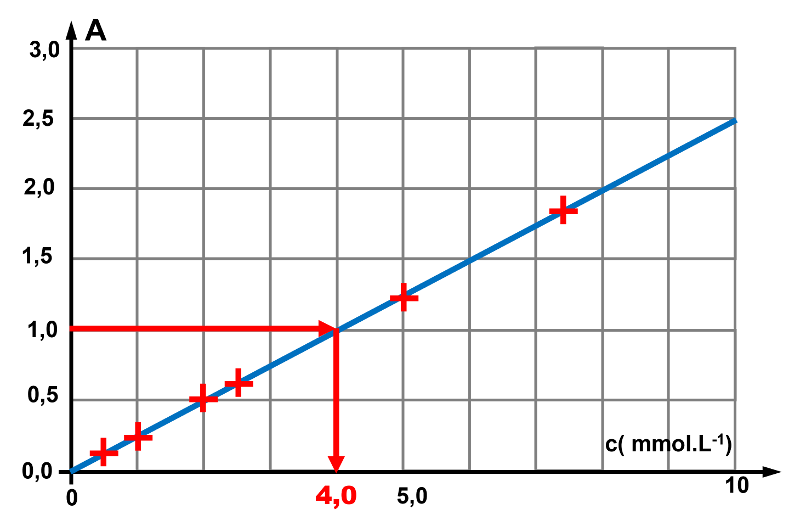
2. Le graphe obtenu est une droite passant par l'origine, l'absorbance est proportionnelle à la concentration (loi de Beer-Lambert).
$A \ = k \times c$
3. LPour une absorbance égale à 1,0, on lit sur le graphe une concentration $c \ = \ 4,0 \ mmol.L^{ \ -1}$.
4. La solution utilisée pour l'étalonnage ayant été diluée 10 fois, la concnetration initiale est : $c_{initiale} \ = \ 10 \times 4,0 \ = \ 40 \ mmolL^{ \ -1}$.
Exercice n°28 : Couleurs d'un indicateur coloré.
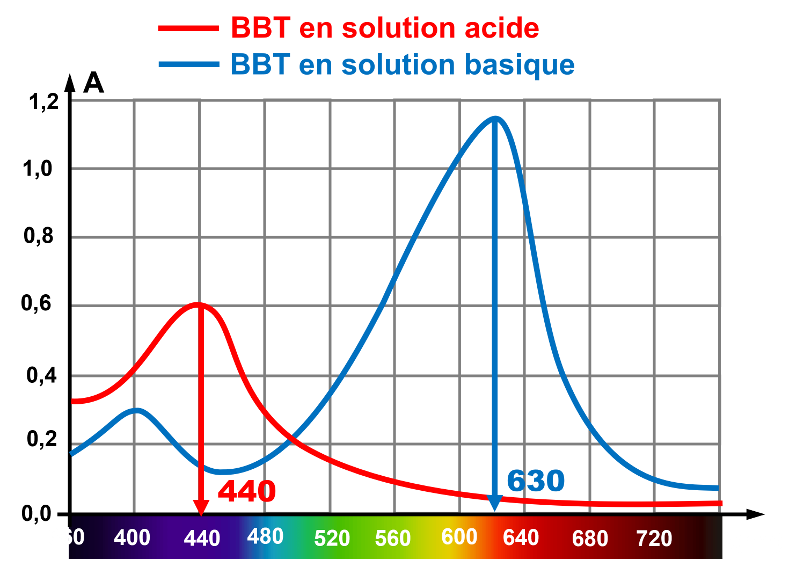
1. En solution acide, le BBT absorbe le vert, le jaune, l'orange et le rouge, transmettant le bleu.
En solution basique, le BBT absorbe le bleu, transmettant le vert, le jaune, l'orange et le rouge.
2. En solution acide, par synthèse additive, le BBT sera jaune.
En solution basique, par synthèse additive, le BBT il sera bleu.
Exercice n°30 : Dosage d'une solution antiseptique de teinture d'iode.
 |
 |
1. On se placera au maximum d'absorbance : $\lambda \ = \ 460 nm$.
2.
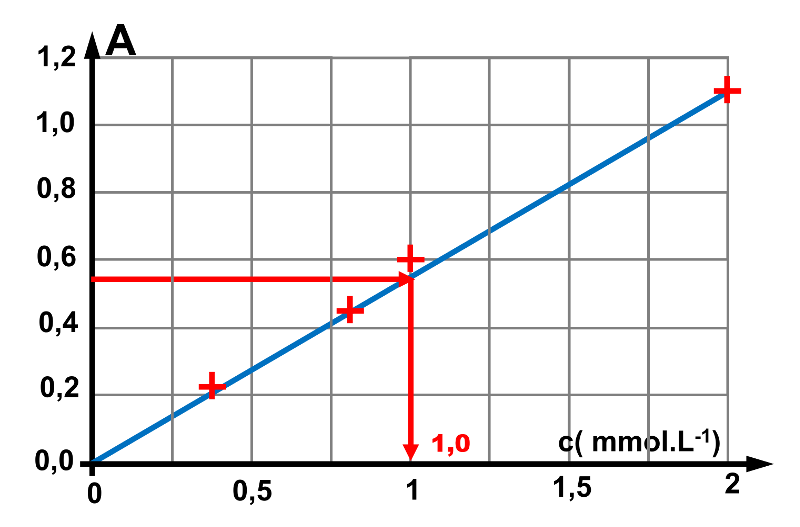
La concentration lue est : $c \ = \ 1,0 \ mmol.L^{ \ -1}$ .
La solution ayant été diluée 200 fois, la solution utilisée avait pour concentration : $c_{initiale} \ = \ 200 \times 1,0 \ = 200 \ mmol.L^{ \ -1}$.
La quantité de matière pélevée est : $n_{prélevée} \ = \ c_{initiale} \times V \ = 200 \times 0,1 \ = \ 20 \ mmol$.
Exercice n°38 : Un acide à minet.
|
1. |
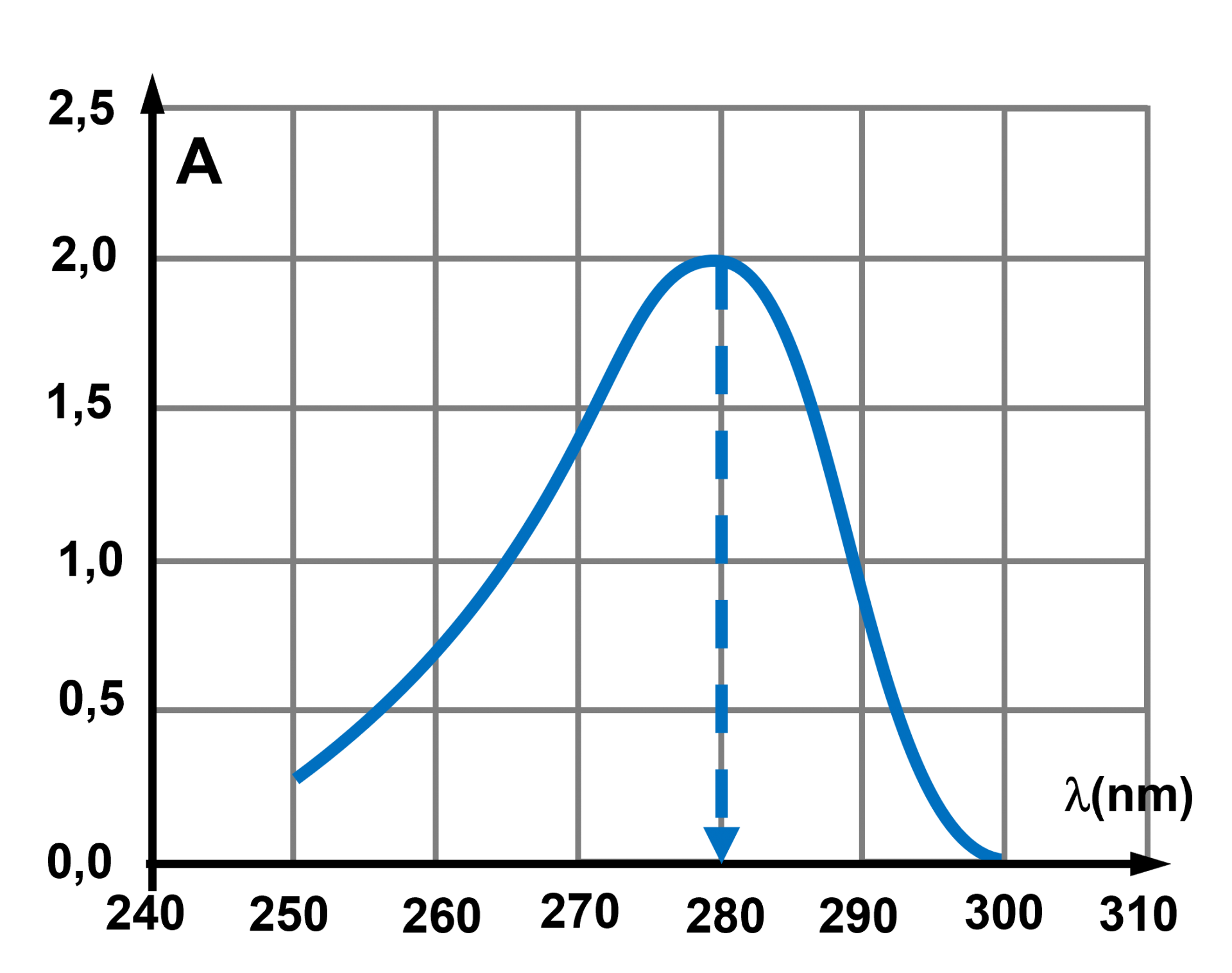 |
Le maximum d'absorption à la longueur d'onde $\lambda \ = \ 280 \ nm$ se situant dans le domaine ultra-violet, la tyrosine est incolore. |
2. Le rapport des concentrations $\dfrac {c_3}{c_4} = \dfrac {1,0.10^{ \ -3}}{5,0.10^{ \ -4}} \ = \ 2$, il faut diluer la solution $S_3$ deux fois. Pour préparer 100 mL de la solution $S_4$, il faut donc prélever $50 \ mL$ de la solution $S_3$ à l'aide d'une pipette jaugée à $50 \ mL$, les introduire dans une fiole jaugée à $100 \ mL$, puis compléter la fiole au trait de jauge.
3. Il faudra :
a : élalonner l'appareil (faire le blanc à l'aide d'une solution d'eau distillée et le noir sans lumière)
b : effectuer les mesure à la longueur d'onde du maximum d'absorbance $\lambda \ = \ 280 \ nm$.
|
4. |
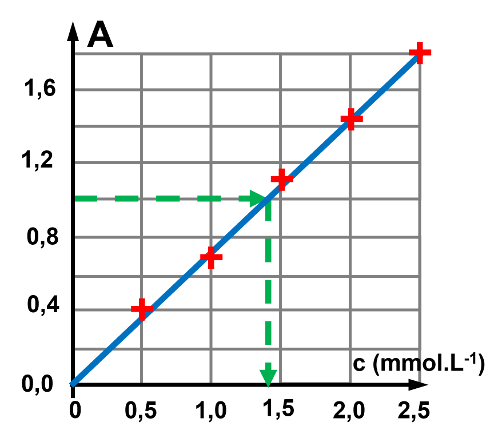 |
La courbe obtenue est une droite passant par l'origine, l'absorbance est proportionnelle à la concentration. L'équation de la droite est : $A \ = \ \dfrac{1,8}{2,5} \times \ c$. Pour une absorbance $A \ = \ 1 $, on a alors $c \ = \ \dfrac {1}{1,8/2,5} \ = 1,39 \ mmol.L^{ \ -1}$ |
La quantité de matière en tyrosine est : $n \ = \ c \times V \ = \ 1,39 \times 2,00 \ = \ 2,78 \ mmol$
La masse de tyrosine dans le comprimé est donc : $m \ = \ n \times M \ = \ 2,78.10^{ \ -3} \times \left (9 \times 12,0 + 11 \times 1,0 + 1 \times 14,0 + 3 \times 16,0 \right ) \ = \ 502,8.10^{ \ -3} \ g$.
Soit $502,8 \ mg$.
5. L'erreur est de $ \dfrac {|502,8-500|}{500} \ = \ 0,6 \ \%$.
Compte tenu des erreurs de manipulation, le résultat est conforme aux indications de l'étiquette.
Exercice n°40 P36 : Un bain pour les poissons.
|
1a. |
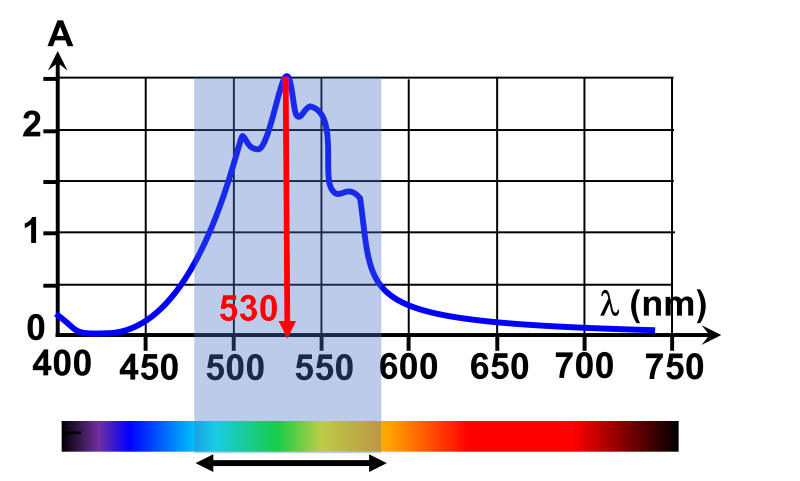 |
La solution absorbe en majorité dans le domaine du vert. Elle renvoie dont le rouge et le bleu. Elle apparaît magenta |
1b.On devra régler le spectrophotomètre à la longueur d'onde correspondant au maximum d'absorbance : $ \lambda \ = 530 \ nm$
|
2. |
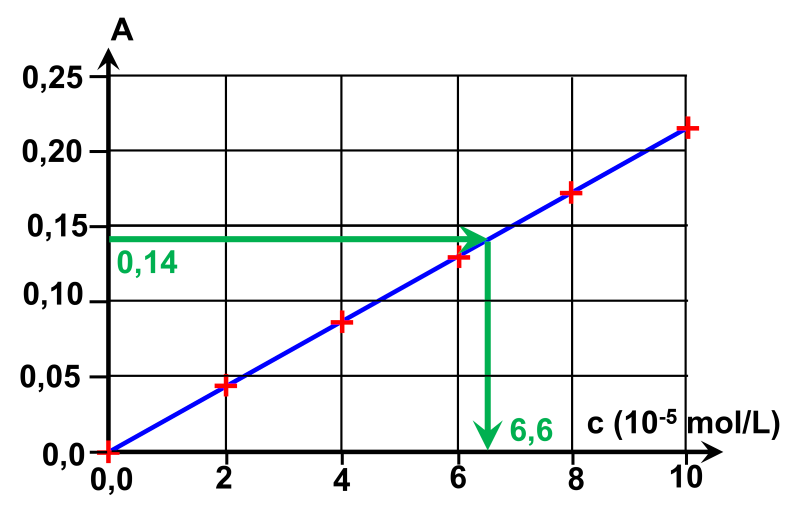 |
Graphiquement, on lit une conentration : $c \ = \ 6,6.10^{ \ -5} \ mol/L$ |
3.La concentration massique préconisée en $KMnO_4$ est : $c_m = \dfrac{1,00}{100} = 1,00.10^{ \ -2} g/L$
La masse molaire du permanganate de potassum est : $M \left ( KMnO_4 \right ) = 1 \times 39,1 + 1 \times 54,9 + 4 \times 16,0 = 158,0 \ g/mol$
La concentration massique correspondant à la concentration molaire définie précédemment est : $c_m \ = M \times c = 158,0 \times 6,6.10^{ \ -5} = 1,04.10^{ \ -2} g/L$
Le bain est conforme.
Ajouter un commentaire
