Sens spontané d'évolution en chimie

EXERCICE n° 13 P 147 : Transformations totales ou non totales ?

a. L'utilisation de la flèche double se fait dans le cas d'une réaction qui n'est pas totale.

b. La disparition totale d'un réactif montre que la réaction est totale. Mais cependant, tous les réactifs n'ont pas totalement disparu si l'un d'eux a été introduit en excès.

c. Lors d'une réaction totale, au moins un des deux réactifs a disparu totalement. Si les réactifs n'ont été introduits dans les conditions stoechiométriques, il restera dans le milieu réactionnel avec les produits. Si les réactifs et les produits coexistent, c'est que la réaction n'est pas totale.

d. Dans le cas d'une réaction totale, le taux d'avancement final est égal à 100%.

e. Lors d'une réaction totale, les réactifs ne réagissent pas entre eux. Ou en tous cas, cette réaction ne crée pas les réactifs initialement introduits.

EXERCICE n° 14 P 147 : Etude graphique

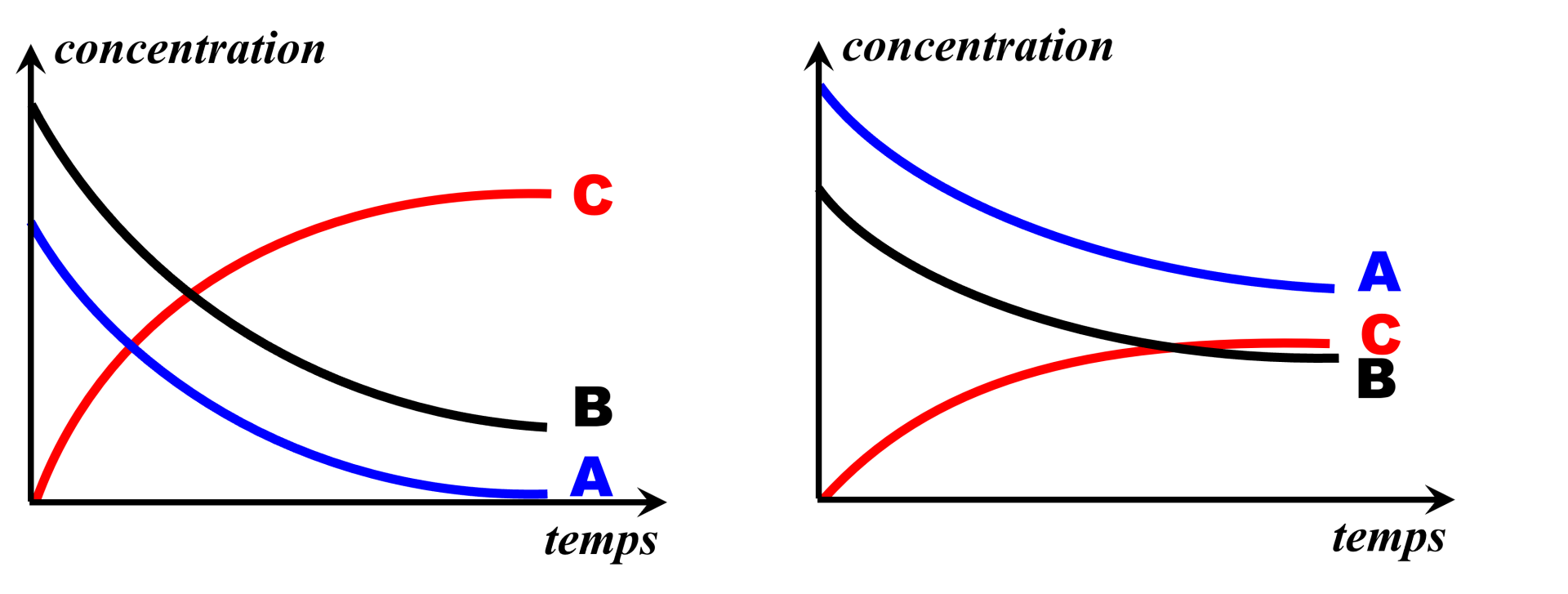
$A \ + \ B \ \longrightarrow \ C$

Transformation 1	Transformation 2

Une réaction totale implique la disparition complète d'au moins un des réactifs. C'est uniquement le cas dans la "transformation 1" : il ne reste plus de réactif $A$.

EXERCICE n° 15 P 147 : Différents états finaux possibles.

$A \ + \ B \ $\overleftarrow{\longrightarrow}$\ C \ + \ D$

Etats finaux possibles :

Une réaction totale implique la disparition complète d'au moins un des réactifs. C'est uniquement le cas dans "l'état final 1" : il ne reste plus de réactif $B$.

EXERCICE n° 17 P 147 : L'acide propanoïque.

1.

$$ \begin{array} { | c | c | c | c | c | c | } Réaction \ : & \ C_2H_5CO_2H_{(l)} & \ + \ H_2O_{(l)} \ & \overrightarrow{\longleftarrow} & C_2H_5CO^{ \ -}_{2(aq)} & \ + \ H_3O^{ \ + }_{(aq)} \\ t_{initial} \ & \ n_0 \ = \ 0,15 \ mol & solvant & & 0 & 0 \\ t \ & n_0 \ = \ 0,15 - x & solvant & & x & x \\ t_{final} \ & n_0 \ = \ 0,15 - x_f & solvant & & x_f & x_f \\ \end{array} $$

2.

L'avancement final est la valeur de la quantité de matière obtenue en ions $H_3O^{ \ +}$ : $x_f \ = \ 1,26.10^{ \ -3} \ mol$

L'avancement maximal est celui qui aurait été obtenu si la réaction était totale. L'acide propanoïque aurait totalement disparu, et on aurait : $x_{max} \ = \ 0,15 \ mol$

3. Le taux d'avancement final est donc : $\tau \ = \ \dfrac{1,26.10^{ \ -3}}{0,15} \ = \ 8,4.10^{ \ -3}$.

4.

A l'état final, il reste : $n_f \left ( C_2H_5CO_2H_{(l)} \right ) \ = \ 0,15 \ - \ 1,26.10^{ \ -3} \ = \ 0,15 \ mol$.

On a produit : $n \left ( C_2H_5CO^{ \ -}_{2(aq)} \right ) \ = \ n \left (H_3O^{ \ + }_{(aq)} \right ) \ = \ 1,26.10^{ \ -3} \ mol$.

5. Si la réaction avait été totale, il ne resterait plus d'acide propanoïque, on aurait un taux d'avancement $\tau \ = \ 1$.

EXERCICE n° 19 P 148 : Quotients de réaction.

EXERCICE n° 21 P 148 : Système à l'équilibre.

$HSO_{3(aq)}^{ \ -} \ + \ HS^{ \ - }_{(aq)} \ \overrightarrow{\longleftarrow} \ SO_{3(aq)}^{ \ 2-} \ + \ H_2S_{(aq)}$

$Q_r \ = \ \dfrac{ \left [ SO_{3(q)}^{ \ 2-} \right ] \times \left [SO_{3(q)}^{ \ 2-} \right ] }{ \left [HSO_{3(aq)}^{ \ -} \right ] \times \left [ HS^{ \ - }_{(aq)} \right ]}$

$K(T) \ = \ 0,630$

1.

$Q_{r,1} \ = \ \dfrac{0,300 \times 0,300}{0,300 \times 0,300} \ = \ 1$

$Q_{r,2} \ = \ \dfrac{0,177\times 0,301}{0,379 \times 0,223} \ = \ 0,630$

$Q_{r,3} \ = \ \dfrac{0,120\times 0,120}{0,326 \times 0,245} \ = \ 0,180$

2.

Dans le premier cas, $Q_{r,1} \ > \ K(T)$. Le système évolue dans le sens indirect.

Dans le deuxième cas, $Q_{r,2} \ = \ 0,630 \ = \ K(T)$, le système n'évolue pas, il est à l'équilibre.

Dans le troisième cas, $Q_{r,3} \ = \ 0,180 \ < \ K(T)$, le système évolue dans le sens direct.

EXERCICE n° 22 P 148 : Prévoir le sens d'évolution.

$ \ 2 \ Fe_{(aq)}^{ \ 3+} \ + \ 2 \  I^{ \ - }_{(aq)} \ \overrightarrow{\longleftarrow} \ 2 \ Fe_{(aq)}^{ \ 2+} \ + \ I_{2(aq)}$

$K(T) \ = \ 5,0.10^{ \ 4}$

1. $K \ = \ \dfrac{ \left [ Fe_{(aq)}^{ \ 2+} \right ]^2 \times \left [ I_{2(aq)} \right ] }{ \left [Fe_{(aq)}^{ \ 3+} \right ]^2 \times \left [ I^{ \ - }_{(aq)} \right ]^2}$

2.

Dans le premier cas : $Q_{r1} \ = \ \dfrac{ \left (1,2.10^{ \ -1} \right )^2 \times \left ( 3,0.10^{ \ -3} \right ) }{ \left ( 4,1.10^{ \ -3} \right )^2 \times \left ( 2,5.10^{ \ -3 }_{(aq)} \right )^2} \ = \ 4,1.10^{ \ 5} \ > \ K(T)$, le système évolue dans le sens indirect.

Dans le deuxième cas : $Q_{r2} \ = \ \dfrac{ \left (6,2.10^{ \ -2} \right )^2 \times \left ( 2,1.10^{ \ -2} \right ) }{ \left ( 9,2.10^{ \ -3} \right )^2 \times \left ( 4,3.10^{ \ -3 }_{(aq)} \right )^2} \ = \ 4,9.10^{ \ 4} \ < \ K(T)$, le système évolue dans le sens direct.

Dans le troisième cas : $Q_{r3} \ = \ \dfrac{ 0,18^2 \times 0,11 }{ \left ( 4,0.10^{ \ -2} \right )^2 \times \left ( 2,5.10^{ \ -2 }_{(aq)} \right )^2} \ = \ 3,6.10^{ \ 3} \ < \ K(T)$, le système évolue dans le sens direct.

EXERCICE n° 29 P 150 : l'arôme de lavande.

1.

$ \begin{array}{|c|c|c c c c c|} \hline Etat & Avc^t & C_2H_4O{2,(l)} \ \ + & C_{10}H_{18}O{(l)} \ & \overleftarrow{\longrightarrow} & C_{12}H_{20}O{2,(l)} \ + & H_2O_{(l)} \\ \hline \hline Etat & Avc^t & Acide \ \ & linalol \ & & A & eau \\ \hline \hline initial & t=0 & n_A = n_L & n_L =n_A & & 0 & 0 \\ \hline \hline instant t & t & n_A - x & n_L -x & & x & x \\ \hline \hline final & t_{final} & n_A - x_f & n_L -x_f & & x_f & x_f \\ \hline \end{array} $

A l'instant $t_1$, les quantités de matière sont :

Pour l'acide : $n_{acide} \ = \ 1,00 - x \ = 1,00 - n_A \ = \ 1-2,35.10^{ \ -4} = 1,00 \ mol$

Pour l'alcool : $n_{alcool} \ = \ 1,00 - x \ = 1,00 - n_A \ = \ 1-2,35.10^{ \ -4} = 1,00 \ mol$

Pour l'acétate de linalol : $n_{A} \ = \ 2,35.10^{ \ -4} \ mol$

Pour l'eau : $n_{eau} \ = \ 2,35.10^{ \ -4} \ mol$

2.

$Q_{r} \ = \ \dfrac{\left [ eau \right ] \times \left [ A \right ]}{\left [ Acide \right ] \times \left [ linalol \right ]} $

NB : ici, l'eau n'est pas un solvant, les espèces sont introduites à l'état pur. Il s'agit d'un produit.

$Q_{r} \ = \ Q_{r} \ = \ \dfrac{\dfrac{n_{A}}{V} \times \dfrac{n_{eau}}{V}}{\dfrac{n_{acide}}{V} \times \dfrac{n_{alcool}}{V}} \ = \ \dfrac{n_{eau} \times n_{A}}{n_{acide} \times n_{linalol}} \ = \ \dfrac{2,35.10^{ \ -4} \times 2,35.10^{ \ -4}}{1 \times 1} \ = \ 5,48.10^{ \ -8}$

3.

$Q_{r} \ < \ K(T) $. L'état d'équilibre n'est pas atteint.

4.

A l'état final, $n_A \ = \ x_f \ = \ 9,87.10^{ \ -3} \ mol$

Au maximum, l'avancement maximal serait : $x_{max} \ = \ 1,0 \ mol$

Le taux d'avancement est : $\tau \ = \ \dfrac{x_f}{x_{max}} \ = \ \dfrac{9,87.10^{ \ -3}}{1,0} \ = \ 9,87.10^{ \ -3} \ < \ 1$. La réaction n'est pas totale.

EXERCICE n° 26 P 149 : Usure d'une pile.

1.

$$ \begin{array} { c c c c } \ Ag^{ \ +}_{(aq)} & \ + \ e^{ \ - } \ & \overrightarrow{\longleftarrow} & Ag_{(s)} \\ & \ Cd_{(s)}& \overrightarrow{\longleftarrow} & Cd^{ \ 2+}_{(aq)} & \ + \ 2 \ e^{ \ -} \\ \hline \ 2 \ Ag^{ \ +}_{(aq)} & + \ Cd_{(s)} & \overrightarrow{\longleftarrow} & 2 \ Ag_{(s)} & + \ Cd^{ \ 2+}_{(aq)} \\ \end{array} $$

2.

$$ \begin{array} { | c | c | c | c | c | } Réaction \ : & \ 2 \ Ag^{ \ +}_{(aq)} & + \ Cd_{(s)} & \overrightarrow{\longleftarrow} & 2 \ Ag_{(s)} & + \ Cd^{ \ 2+}_{(aq)} \\ \hline t_i \ : & n_1 & n_2 & & 0 & 0 \\ t \ : & n_1 - 2x & n_2-x & & 2x & x \\ t_f \ : & n_1 - 2x_f & n_2-x_f & & 2x_f & x_f \\ \end{array} $$

A l'état initial, la quantité en ions argent $Ag^{ \ +}$ est : $n_1 \ = \ C \times V \ = 0,15 \times 0,25 \ = 3,75.10^{ \ -2 } \ mol$

A l'état initial, la quantité en cadmium $Cd$ est : $n_2 \ = \ \dfrac{m}{M} \ = \ \dfrac{30}{112,4} \ = \ 0,27 \ mol$

La réaction s'arrêtera lorsque qu'un des deux réactifs aura totalement disparu :

$$ \begin{cases} \ n_1 - 2x_f \ = \ 0 \\ ou \\ \ n_2 -x_f \ = \ 0 \end{cases} \Leftrightarrow \begin{cases} \ x_f \ = \ \dfrac{n_1}{2} \ = \ 1,88.10^{ \ -2} \ mol \\ ou \\ \ x_f \ = \ n_2 \ = \ 2,7.10^{ \ -1} \ mol \end{cases} $$

Le réactif limitant est $Ag^{ \ +} $

3. La capacité de la pile est donc : $Q \ = \ 2 \times \dfrac{n_1}{2} \times N_a \times e \ =  \ 2 \times \ 1,88.10^{ \ -2 } \times 6,02.10^{ \ 23} \times 1,6.10^{ \ -19} \ = \ 3612 \ C$

EXERCICE n° 34 P 152 : Synthèse d'un arôme de poire.

Dans le cas de la première réaction.

1.

$ \begin{array}{|c|c|c c c c c|} \hline Etat & Avc^t & C_2H_4O{2,(l)} \ \ + & C_{3}H_{8}O{(l)} \ & \overleftarrow{\longrightarrow} & C_{5}H_{10}O{2,(l)} \ + & H_2O_{(l)} \\ \hline initial & t=0 & n_{ac} & n_{al} & & 0 & 0 \\ \hline \hline instant t & t & n_{ac} - x & n_{al} -x & & x & x \\ \hline \hline final & t_{final} & n_{ac}- x_f & n_{al} -x_f & & x_f & x_f \\ \hline \end{array} $

2.

Les quantités de matière initiales sont :

$n_{ac} \ = \ \dfrac{m}{M} \ = \ \dfrac{15,0}{60} \ = \ 0,25 \ mol$

$n_{al} \ = \ \dfrac{m}{M} \ = \ \dfrac{12,0}{60} \ = \ 0,20 \ mol$

La réaction s'arrêtera si l'un des deux réactifs a totalement disparu :

$ \begin{array}{c c c } \left \{ \begin {array}{l} n_{ac} - x_{max} = 0 \\ n_{al} -x_{max} =0 \end{array} \right. & \Leftrightarrow & \left \{ \begin {array}{l} x_{max} = 0,25 \ mol\\ x_{max} = 0,20 \ mol \end{array} \right. \end{array} $

Ici, l'alcool est limitant, et $x_{max} \ = \ 0,20 \ mol$

On obtient une quantité de matière en éthanoate de propyle : $n_{ester} \ = \ \dfrac{m}{M} \ = \ \dfrac{11,6}{102} \ = \ 0,11 \ mol$

L'avancement final est : $\tau \ = \ \dfrac{x_f}{x_{max}} \ = \ \dfrac{0,11}{0,20} \ = \ 0,57$

3.

Dans ce cas, la réaction n'étant pas totale, le symbole de la flèche double est correct.

Dans le cas de la deuxième réaction.

1.

$ \begin{array}{|c|c|c c c c c|} \hline Etat & Avc^t & C_4H_6O{3,(l)} \ \ + & C_{3}H_{8}O{(l)} \ & \overleftarrow{\longrightarrow} & C_{5}H_{10}O{2,(l)} \ + & C_2H_4O_2{(l)} \\ \hline initial & t=0 & n_{ac} & n_{al} & & 0 & 0 \\ \hline \hline instant t & t & n_{ac} - x & n_{al} -x & & x & x \\ \hline \hline final & t_{final} & n_{ac}- x_f & n_{al} -x_f & & x_f & x_f \\ \hline \end{array} $

2.

Les quantités de matière initiales sont :

$n_{ac} \ = \ \dfrac{m}{M} \ = \ \dfrac{30,6}{102} \ = \ 0,30 \ mol$

$n_{al} \ = \ \dfrac{m}{M} \ = \ \dfrac{9,0}{60} \ = \ 0,15 \ mol$

La réaction s'arrêtera si l'un des deux réactifs a totalement disparu :

$ \begin{array}{c c c } \left \{ \begin {array}{l} n_{ac} - x_{max} = 0 \\ n_{al} -x_{max} =0 \end{array} \right. & \Leftrightarrow & \left \{ \begin {array}{l} x_{max} = 0,30 \ mol\\ x_{max} = 0,15.10^{ \ -1} \ mol \end{array} \right. \end{array} $

Ici, l'alcool est limitant, et $x_{max} \ = \ 0,15.10^{ \ -1} \ mol$

On obtient une quantité de matière en éthanoate de propyle : $n_{ester} \ = \ \dfrac{m}{M} \ = \ \dfrac{15,3}{102} \ = \ 0,15 \ mol$

L'avancement final est : $\tau \ = \ \dfrac{x_f}{x_{max}} \ = \ \dfrac{0,15}{0,15} \ = \ 1$

3.

Dans ce cas, la réaction est totale, le symbole de la flèche double n'est pas correct.

EXERCICE n° 35 P 152 : Conductivité du vinaigre.

1a,b,c.

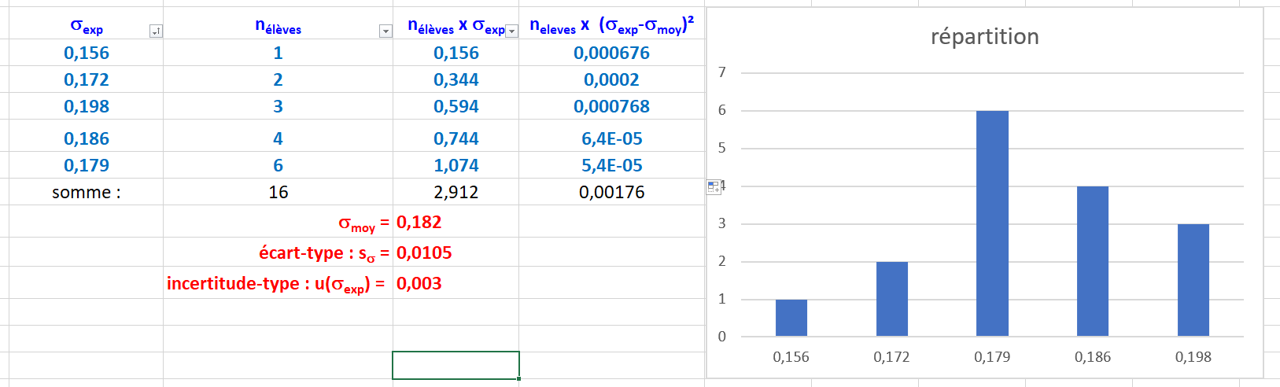
1d.

La dispersion est liée aux conditions expérimentales : étalonnage, précision de la dilution, propreté de la verrerie... Elle est aussi liée aux conditions techniques : tolérance de l'appareil.

Ici, l'incertitude-type : $\dfrac{u(\sigma_{exp}}{\bar{\sigma_exp}} \ = \ \dfrac{0,003}{0,182} \ = 1,6 \ %$

Cette valeur est inférieure à $10 \ %$. La dispersion est correcte.

2,3.

$ \begin{array}{|c|c|c c c c c|} \hline Etat & Avc^t & CH_3CO{2,(l)} \ \ + & H_{2}O{(l)} \ & \overleftarrow{\longrightarrow} & CH_{3}CO{2,(aq)}^{ \ -} \ + & H_3O_{(aq)}^{ \ +} \\ \hline initial & t=0 & 0,13 & excès & & 0 & 0 \\ \hline \hline instant t & t & 0,13 - x & excès & & x & x \\ \hline \hline final & t_{final} & 0,13- x_f & excès & & x_f & x_f \\ \hline \hline max & t & 0,13 - x_{max} & excès & & x_{max} & x_{max} \\ \hline  \end{array} $

4.

Attention : la solution a été diluée 10 fois : la concentration est $0,13 \ mol.L^{ \ -1}$. Cette concentration est exprimée en $mol.L^{ \ -1}$, il faut la convertir en $mol.m^{ \ -3}$ : $c \ = \ 0,13.10^{ \ 3} \ mol.m^{ \ -3}$

$\sigma_{th} \ = \ \lambda_{CH_3CO_2^{ \ -}} \times \left [ CH_3CO_2^{ \ -} \right ] \ + \ \lambda_{H_3O{ \ +}} \times \left [ H_3O{ \ +} \right ]$

$\sigma_{th} \ = \ 4,3.10^{ \ -3} \times 0,13.10^{ \ 3} \ + \ 3,5.10^{ \ -2} \times 0,13.10^{ \ 3} \ = \ 5,1 \ S.m^{ \ -1}$

5.

Les valeurs mesurées sont totalement différentes de la valeur théorique. La supposition d'une réaction totale n'est pas correcte.

6.

La réaction n'étant pas totale, on aura : $\tau \ < \ 1$.

7.

$\sigma_{exp} \ = \ \left ( \lambda_{CH_3CO_2^{ \ -}} + \lambda_{H_3O{ \ +}} \right ) \times \dfrac{x_f}{V}$.

$\Leftrightarrow x_f \ = \dfrac{\sigma_{exp} \times V}{\lambda_{CH_3CO_2^{ \ -}} + \lambda_{H_3O^{ \ +}}} \ = \ \dfrac{0,182 \times 10^{ \ - 3}}{4,1.10^{ \ -3} + 3,5.10^{\ -2}} \ = \ 4,7.10^{ \ -3} \ mol$.

Alors : $\tau \ = \ \dfrac{x_f}{x_{max}} \ = \ \dfrac{4,7.10^{ \ -3}}{0,13} \ = 3,6 \ %$.

La réaction n'est pas totale, comme indiqué en 5.